4. SCATTERING OF LIGHT BY DUST: DIELECTRIC FUNCTIONS

The light scattering properties of dust are usually evaluated based on its optical properties (i.e. dielectric functions or indices of refraction) and geometry (i.e. size and shape) by solving the Maxwell equations

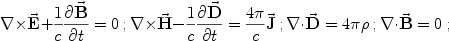(11)

where E is the electric field, B is the magnetic induction, H is the magnetic field, D is the electric displacement, J is the electric current density, and is the electric charge density. They are supplemented with the constitutive relations (or "material relations")

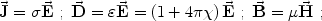(12)

where is the electric conductivity, = 1 + 4 is the dielectric function (or permittivity or dielectric permeability), is the electric susceptibility, and µ is the magnetic permeability. For time-harmonic fields E, H exp(-i t), the Maxwell equations are reduced to the Helmholtz wave equations

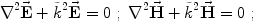(13)

where 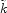= m / c is the complex wavenumber, m = (µ( + i 4 / ))^1/2 is the complex refractive index, and = 2 c / is the circular frequency. These equations should be considered for the field outside the dust (which is the superposition of the incident field and the scattered field) and the field inside the dust, together with the boundary conditions (i.e. any tangential and normal components of E are continuous across the dust boundary). For non-magnetic dust (µ = 1), the complex refractive index is m = ( + i 4 / )^1/2. For non-magnetic, non-conducting dust, m = ()^1/2 For highly-conducting dust, 4 / >> 1, therefore, both the real part and the imaginary part of the index of refraction are approximately (2 / )^1/2 at long wavelengths.

The complex refractive indices m or dielectric functions of dust are often called optical constants, although they are not constant but vary with wavelengths. They are of great importance in studying the absorption and scattering of light by dust. They are written in the form of m = m' + i m" and = ' + i '. The sign of the imaginary part of m or is opposite to that of the time-dependent term of the harmonically variable fields [i.e. m", " > 0 for E, H exp(-i t); m", " < 0 for E, H exp(i t)]. The imaginary part of the index of refraction characterizes the attenuation of the wave (4m" / is called the absorption coefficient), while the real part determines the phase velocity (c / m') of the wave in the medium: for an electric field propagating in an absorbing medium of m = m' + i m", say, in the x direction, E exp(- m" x / c) exp[-i (t - m' x / c)].

The physical basis of the dielectric function can readily be understood in terms of the classical Lorentz harmonic oscillator model (for insulators) and the Drude model (for free-electron metals). In the Lorentz oscillator model, the bound electrons and ions of a dust grain are treated as simple harmonic oscillators subject to the driving force of an applied electromagnetic field. The applied field distorts the charge distribution and therefore produces an induced dipole moment. To estimate the induced moments we consider a (polarizable) grain as a collection of identical, independent, isotropic, harmonic oscillators with mass m and charge q; each oscillator is under the action of three forces: (i) a restoring force -Kx, where K is the force constant (i.e. stiffness) of the "spring" to which the bound charges are attached, and x is the displacement of the bound charges from their equilibrium; (ii) a damping force -b, where b is the damping constant; and (iii) a driving force qE produced by the (local) electric field E. The equation of motion of the oscillators is

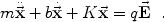(14)

For time harmonic electric fields E exp(-i t), we solve for the displacement

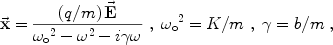(15)

where _o is the frequency of oscillation about equilibrium (i.e. the restoring force is -m _o² x). The induced dipole moment p of an oscillator is p = qx. Let n be the number of oscillators per unit volume. The polarization (i.e. dipole moment per unit volume) P = np = nqx is

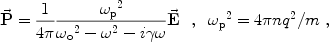(16)

where _p is the plasma frequency. Since P = E = ( - 1) / 4E, the dielectric function for a one-oscillator model around a resonance frequency _o is

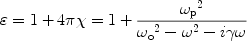	(17)
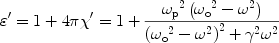	(18)
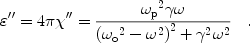	(19)

We see from Eq. 19 " 0 for all frequencies. This is true for materials close to thermodynamic equilibrium, except those with population inversions. If there are many oscillators of different frequencies, the dielectric function for a multiple-oscillator model is

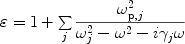(20)

where _p,j, _j and _j are respectively the plasma frequency, the resonant frequency, and the damping constant of the j-th oscillator.

The optical properties associated with free electrons are described by the Drude model. The free electrons experience no restoring forces when driven by the electric field of a light wave and do not have natural resonant frequencies (i.e. _o = 0). The Drude model for metals is obtained directly from the Lorentz model for insulators simply by setting the restoring force in Eq. 14 equal to zero. The dielectric function for free electrons is

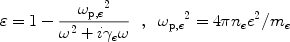	(21)
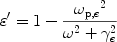	(22)
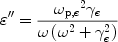	(23)

where _p,e is the plasma frequency, n_e is the density of free electrons and m_e is the effective mass of an electron. The damping constant _e = 1 / _e is the reciprocal of the mean free time between collisions (_e) which are often determined by electron-phonon scattering (i.e. interaction of the electrons with lattice vibrations). ⁵ For dust materials (e.g. graphite) containing both bound charges and free electrons, the dielectric function is

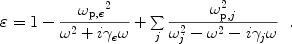(24)

The optical response of free electrons in metals can also be understood in terms of the electric current density J and conductivity (). The free electrons in metals move between molecules. In the absence of an external field, they move in a random manner and hence they do not give rise to a net current flow. When an external field is applied, the free electrons acquire an additional velocity and their motion becomes more orderly which gives rise to an induced current flow. The current density J = -n_e e is obtained by solving the equation of motion of the free electrons m_e = -eE - m_e / _e

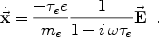(25)

Since J = E, the a.c. conductivity is = _o / (1 - i _e), where _o = n_{e e} e² / m_e is the d.c. conductivity. The dielectric function for a free-electron metal is therefore

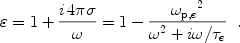(26)

The real and imaginary parts of the dielectric function are not independent. They are related through the Kramers-Kronig (or dispersion) relations

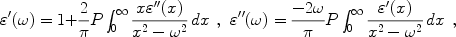(27)

where P is the Cauchy Principal value of the integral

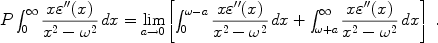(28)

The real and imaginary parts of the index of refraction are also connected through the Kramers-Kronig relation. This also holds for the real and imaginary parts of the electric susceptibility.

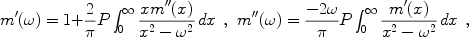	(29)
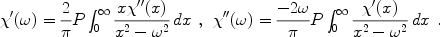	(30)

The Kramers-Kronig relation can be used to relate the extinction cross section integrated over the entire wavelength range to the dust volume V

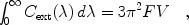(31)

where F, a dimensionless factor, is the orientationally-averaged polarizability relative to the polarizability of an equal-volume conducting sphere, depending only upon the grain shape and the static (zero-frequency) dielectric constant _o of the grain material [64]. This has also been used to place constraints on interstellar grain models based on the interstellar depletions [46, 50] and the carrier of the mysterious 21 µm emission feature seen in 12 protoplanetary nebulae [44].

For illustration, we show in Figure 3 the refractive indices of glassy SiO₂ and neutral and singly-charged silicon nanoparticles (SNPs). ⁶ The optical properties of SNPs depend on whether any free electrons or holes are present. The contribution of free electrons or holes to the dielectric function of SNPs is approximated by δ -_p^{2 2}/ (^{2 2} + i ), _p² = 3|Z|e² / a³ m_eff, where e is the proton charge, Ze is the grain charge, a is the grain radius, a / v_F is the collision time (we take v_F 10⁸cm s^-1), and m_eff is the effective mass of a free electron or hole. In Figure 3 the charged SNPs are taken to contain only one hole (i.e. Z = +1). We take m_eff 0.2 m_e.

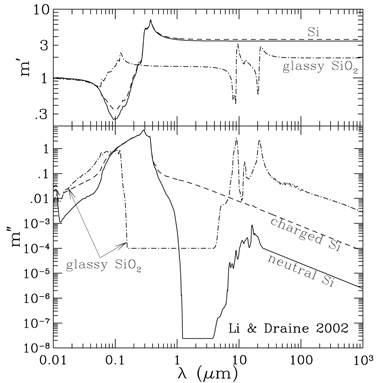Figure 3. Refractive indices m' (upper panel), m" (lower panel) of neutral silicon nanoparticles (Si; solid lines), singly, positively charged (Z = +1) silicon nanoparticles of size a = 10 Å (dashed lines), and SiO2 glass (dot-dashed lines). Compared to neutral Si, in charged Si free electrons (if negative charged) or holes (if positively charged) contribute to the dielectric function. Crystalline Si is IR inactive since its lattice vibrations have no dipole moment; the bands at 6.91, 7.03, 7.68, 8.9, 11.2, 13.5, 14.5, 16.4, and 17.9µm are due to multi-phonon processes. Taken from [48].

⁵ For nano-sized metallic dust (which is smaller than the mean free path of conduction electrons in the bulk metal), _e and _e are increased because of additional collisions with the boundary of the dust: _e = _bulk + v_F / ( a), where _bulk is the bulk metal damping constant, v_F is the electron velocity at the Fermi surface, is a dimensionless constant of order unity which depends on the character of the scattering at the boundary ( a is the effective mean free path for collisions with the boundary): = 1 for classic isotropic scattering, = 4/3 for classic diffusive scattering, = 1.16 or = 1.33 for scattering based on the quantum particle-in-a-box model (see [9] and references therein). Since ² >> _e² in metals near the plasma frequency, " can be written as " = "_bulk + v_{F p}² / ( a ³). This, known as the "electron mean free path limitation" effect, indicates that for a metallic grain " increases as the grain becomes smaller. Back.

⁶ SNPs were proposed as the carrier of the "extended red emission" (ERE), a broad, featureless emission band between ~ 5400 and 9000 Å seen in a wide variety of dusty environments [72, 41] (but see [48]). SNPs were also suggested to be present in the inner corona of the Sun [24] (but see [54, 55]). Back.