4. DISCUSSION

The cosmic nuclear reactor was active for a brief epoch in the early evolution of the universe. As the Universe expanded and cooled the nuclear reactor shut down after ~ 20 minutes, having synthesized in astrophysically interesting abundances only the lightest nuclides D, ³He, ⁴He, and ⁷Li. For the standard models of cosmology and particle physics (SBBN) the relic abundances of these nuclides depend on only one adjustable parameter, the baryon abundance parameter _B (the post-e ^± annihilation value of the baryon (nucleon) to photon ratio). If the standard models are the correct description of the physics controlling the evolution of the universe, the abundances of the four nuclides should be consistent with a single value of _B and this baryon density parameter should also be consistent with the values inferred from the later evolution of the universe (e.g., at present as well as ~ 400 kyr after BBN, when the relic photons left their imprint on the CBR observed by WMAP and other detectors). There are, however, two other particle physics related cosmological parameters, the lepton asymmetry parameter _e and the expansion rate parameter S, which can affect the BBN-predicted relic abundances. For SBBN it is assumed that _e = 0 and S = 1. Deviations of either or both of these parameters from their standard model expected values could signal new physics beyond the standard model(s).

The simplest strategy is to test first the predictions of SBBN. Agreement between theory and observations would provide support for the standard models. Disagreements are more difficult to interpret in that while they may be opening a window on new physics, they may well be due to unaccounted for systematic errors along the path from observations of post-BBN material to the inferred primordial abundances. Subject to this latter caveat, the confrontation between theory and data can provide useful limits to (some of) the parameters associated with new physics which complement those from high precision, terrestrial experiments. In the comparisons presented below, the abundances (and their inferred uncertainties) presented in Section 3 are adopted and compared to the BBN predictions described by the simple fits from Section 2.2. For ⁴He the SSBN range in _B favored by the adopted primordial abundance lies outside the range of validity of the simple fit; for ⁴He and SBBN, the best fit and uncertainty in _B is derived from the more detailed BBN calculations. While not all models of new physics proposed in the literature can be tested in this manner, this approach does offer the possibility of constraining a large subset of them and of providing a useful framework for understanding qualitatively how many of the others might affect the BBN predictions.

4.1. SBBN

The discussion in Section 3 identifies a set of primordial abundances. Since these choices are certainly subjective and likely to change as more data are acquired, along with a better understanding of and accounting for systematic errors, the analytic fits presented in Section 2.2 can be very useful in relating new conclusions and constraints to those presented here. The abundances and nominal 1 uncertainties adopted here are: y_D = 2.6 ± 0.4, y₃ = 1.1 ± 0.2, Y_P = 0.241 ± 0.004, and y_Li = 2.34_-0.25^+0.29 ([Li]_P = 2.37 ± 0.05). Y_P 0.254 is adopted for an upper bound (at ~ 2) to the primordial ⁴He mass fraction. The corresponding SBBN values of the baryon density parameter are shown in Figure 12, along with that inferred from the CBR and observations of Large Scale Structure [2] (labelled WMAP).

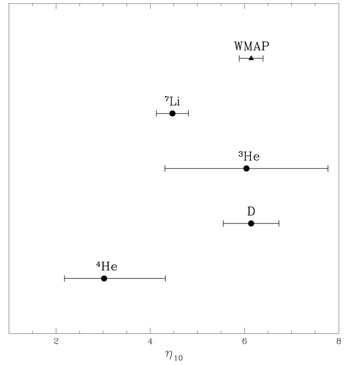Figure 12. The SBBN values for the early universe (~ 20 minutes) baryon abundance parameter 10 inferred from the adopted primordial abundances of D, 3He, 4He, and 7Li (see Section 3.1 - 3.4). Also shown is the WMAP-derived CBR and LSS value (~ 400 kyr).

As Figure 12 reveals, the adopted relic abundances of D and ³He are consistent with the SBBN predictions (_D = 6.1 ± 0.6, _³He = 6.0 ± 1.7) and both are in excellent agreement with the non-BBN value [2] (_WMAP = 6.14 ± 0.25). If the most recent deuterium abundance determination in a high redshift, low metallicty QSOALS [18] is included in estimating the relic D abundance, the mean shifts to a slightly lower value (y_D = 2.4 ± 0.4), corresponding to a slightly higher estimate for the baryon density parameter (_D = 6.4 ± 0.7), which is still consistent with ³He and with WMAP. Were it not for the very large dispersion among the D abundance determinations (see Section 3.1), the formal error in the mean (~ 5%) could have been adopted for the uncertainty in y_D, leading to a ~ 3% determination of _D, competitive with that from WMAP. Due to the very large observational and evolutionary uncertainties associated with ³He, its abundance mainly provides a consistency check at present. Since the variations of its predicted relic abundance with S and _e are similar to those for D, ³He will not add new information to that from D in the comparisons to be discussed below.

In addition to the successes of D and ³He, Figure 12 exposes a tension between WMAP (and D and ³He) and the adopted primordial abundances of ⁴He and ⁷Li. The 1 range determined from ⁴He is low: 2.2 _He 4.3; however, the 2 range is much larger: 1.7 _He 6.4, encompassing the WMAP-inferred baryon density. The ⁷Li inferred baryon density is also low (_Li = 4.5 ± 0.3) and here the adopted errors appear to be far too small to bridge the gap to D and WMAP. These tensions may be a sign of systematic errors introduced when the observational data is used to derive the inferred primordial abundances or, it could be a signal of new physics beyond the standard models of cosmology and particle physics.

4.2. Lithium

As identified above, the SBBN abundances of D and ³He are in agreement with each other and with the non-BBN estimate of the baryon density parameter from Large Scale Structure and the CBR. However, while the inferred primordial abundance of ⁴He is less than 2 away from the SBBN-predicted value, that of lithium differs from expectations by a factor of ~ 2 (or more). It is unlikely that this conflict can be resolved through a non-standard expansion rate (S 1) or a non-zero lepton number (_e 0). The reason is that in the S - _B and _e - _B planes the isoabundance curves for D and ⁷Li are very nearly parallel (see eqs. 16 & 23 in Section 2.2 and Figs. 1 & 2 from Kneller & Steigman [9]), so that once y_D is constrained, there is very little freedom to modify y_Li. This may be seen by combining eqs. 16 & 23 to relate _Li to _D,

(27)

Thus, for _D 6 and |S - 1| 0.1, |_e| 0.1, _{Li D} 6, so that y_Li 4 ([Li]_P 2.6).

Nonetheless, a non-standard physics explanation of the lithium conflict is not ruled out. Indeed, there are models where late-decaying, massive particles reinitiate BBN, modifying the abundances of the light nuclides produced during the first 20 minutes. For an extensive, yet likely incomplete list (with apologies) of references, see Ref. [36] and further references therein. In such models it is quite possible to reduce the original BBN abundance of ⁷Li to bring it into agreement with the value inferred from the observational data [34, 35, 36, 37]. However, it is found that when the many new parameters available to these models are adjusted to achieve this agreement, the modified relic abundance of ³He is much too large (see, e.g., Ellis, Olive, and Vangioni [40]).

The difficulty in reconciling the observed and predicted relic abundances of ⁷Li suggests that the problem may be in the stars. It is not at all unexpected that the very old halo stars where lithium is observed will have modified their original surface abundances, ⁷Li in particular (see Pinsonneault et al. [39] and Charbonnel and Primas [38] for discussions and many additional references). While there is no dearth of physical mechanisms capable of destroying or diluting surface lithium, many of which are supported by independent observational data, the challenge has been to account for the required depletion (factor of 2 - 3) while maintaining a negligible dispersion ( 0.1 dex) among the "Spite plateau" lithium abundances.

Another possibility for reconciling the observed and predicted relic abundances of ⁷Li lies in the nuclear physics. After all, given the estimates of uncertainties in the cross sections of the key nuclear reactions leading to the production and destruction of mass-7, the BBN-predicted abundance of ⁷Li is the most uncertain (~ 10-20%) of all the light nuclides. Perhaps the conflict between theory and observation is the result of an error in the nuclear physics. This possibility was investigated by Cyburt, Fields, and Olive [41] who noted that some of the same nuclear reactions of importance in BBN, play a role in the standard solar model and are constrained by its success in accounting for the observed flux of solar neutrinos. While the uncertainty of a key nuclear reaction (³He(, )⁷Be) is large (~ 30%), it is far smaller than the factor of ~ 3 needed to reconcile the predicted and observationally inferred abundances [41].

Considering the current state of affairs (no successful resolution based on new physics; possible reconciliation based on stellar astrophysics), ⁷Li is not used below where the adopted relic abundances of D and ⁴He are employed to set constraints on S and/or _e.

4.3. Non-Standard Expansion Rate: S 1 (_e = 0)

If the lepton asymmetry is very small, of order the baryon asymmetry, then BBN depends on only two free parameters, _B and S (or N). Since the primordial abundance of D largely probes _B while that of ⁴He is most sensitive to S (see Fig. 2 and eqs. 16 & 20), for each pair of y_D and Y_P values (within reason) there will be a corresponding pair of _B and S values. For the D and ⁴He abundances adopted above (y_D = 2.6 ± 0.4, Y_P = 0.241 ± 0.004) the best fits for _B and S, shown in Figure 13, are for ₁₀ = 5.9 ± 0.6 and S = 0.96 ± 0.02; the latter corresponds to N = 2.5 ± 0.3. These values are completely consistent with those inferred from the joint constraints on S and _B from WMAP [42].

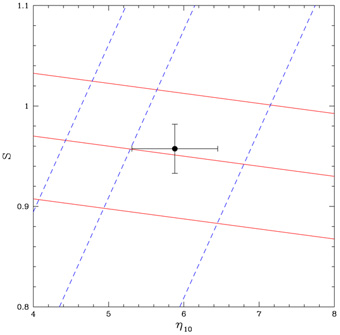Figure 13. The D and 4He isoabundance curves in the S - 10 plane, as in Fig. 2. The best fit point and the error bars correspond to the adopted primordial abundances of D and 4He.

As expected from the discussion in Section 2.2, the lithium abundance is largely driven by the adopted deuterium abundance and is little affected by the small departure from the standard expansion rate. For the above best fit values, y_Li = 4.3 ± 0.9 ([Li]_P = 2.63_-0.10^+0.08). This class of non-standard models (S 1), while reconciling ⁴He with D and with the CBR, is incapable of resolving the lithium conflict.

4.4. Non-Zero Lepton Number: _e 0 (S = 1)

While most popular extensions of the standard model which attempt to account for neutrino masses and mixings suggest a universal lepton asymmetry comparable in magnitude to the baryon asymmetry (_e ~ O(_B) 10^-9) ⁶, there is no direct evidence that nature has made this choice. Although the CBR is blind to a relatively small lepton asymmetry, BBN provides an indirect probe of it [43]. As discussed in Section 1.3 & Section 2, a lepton asymmetry can change the neutron to proton ratio at BBN, modifying the light element yields, especially that of ⁴He. Assuming S = 1 and allowing _e 1, BBN now depends on the two adjustable parameters _B and _e which may be constrained by the primordial abundances of D and ⁴He. Given the strong dependence of Y_P on _e and of y_D on _B, these nuclides offer the most leverage. In Figure 14 are shown the D and ⁴He isoabundance curves (i.e., the fits from Section 2.2) in the _e - _B plane, along with the best fit point (and its 1 uncertainties) determined by the adopted primordial abundances. The best fit baryon abundance, ₁₀ = 6.1 ± 0.6 is virtually identical to the SBBN (and WMAP) value. While the best fit lepton asymmetry, _e = 0.031 ± 0.018, is non-zero, it differs from zero by less than 2 (as it should since the adopted value of Y_P differs from the SBBN expected value by less than 2).

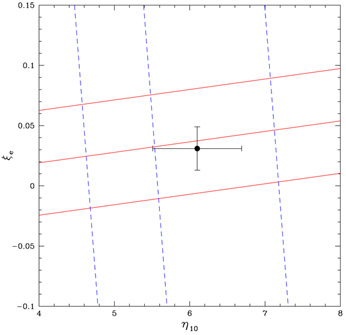Figure 14. The D and 4He isoabundance curves in the e - 10 plane, as in Fig. 3. The best fit point and the error bars correspond to the adopted primordial abundances of D and 4He.

As expected from the discussion above for S 1 and in Section 2.2, here, too, the lithium abundance is largely driven by the adopted deuterium abundance and is little affected by the small lepton asymmetry allowed by D and ⁴He. For the above best fit values, the predicted lithium abundance is virtually identical to the SBBN/WMAP and S 1 values: y_Li = 4.3 ± 0.9 ([Li]_P = 2.64_-0.10^+0.08). A lepton asymmetry which reconciles ⁴He with D cannot resolve the lithium conflict.

4.5. An Example: Alternate Relic Abundances for D and ⁴He

It is highly likely that at least some of the tension between D and ⁴He is due to errors associated with inferring their primordial abundances from the current observational data. As a result, in the future the abundances adopted here may be replaced by revised estimates. This is where the simple, analytic fits derived by KS [9] and presented in Section 2.2 can be of value to those who lack an in-house BBN code. Provided that the revised abundances lie in the ranges 2 y_D 4 and 0.23 Y_P 0.25, these fits will provide quite accurate, back of the envelope estimates of _B, S, _e, and of y_Li. As an illustration, let's revisit the discussion in Section 4.3 & Section 4.4, now adopting for D the weighted mean deuterium abundance which results when the most recent determination [18] is included, y_D = 2.4 ± 0.4 (see Section 3.1), along with, for ⁴He, the helium abundance derived by applying the OS mean offset to the IT-inferred primordial value (see eq. 25) without the icf-correction, Y_P = 0.2472 ± 0.0035 (see Section 3.3). These alternate abundances correspond to _D 6.5 ± 0.7 and _He 5.5 ± 2.2.

For _e = 0, the new values for the expansion rate factor and the baryon density parameter are S = 0.991 ± 0.022 (N = 2.9 ± 0.3) and ₁₀ = 6.4 ± 0.6. While the N estimate is entirely consistent with N = 3, the corresponding ~ 2 upper bound (N 3.5) still excludes even one extra light scalar. The baryon density parameter is slightly higher than, but entirely consistent with that inferred from the CBR. As anticipated from the previous discussion, the predicted lithium abundance hardly changes at all, but it does increase slightly to further exacerbate the conflict with the observationally inferred value, y_Li 4.9 ± 1.1 ([Li]_P = 2.69_-0.11^+0.09).

For S = 0, the new values for the lepton asymmetry parameter and the baryon density parameter are _e = 0.007 ± 0.016 and ₁₀ = 6.5 ± 0.7. The former is consistent with no lepton asymmetry (i.e., with _e ~ O(_B)) and the latter is slightly higher than, but still entirely consistent with the baryon density parameter inferred from the CBR. As expected, here, too, the predicted lithium abundance increases slightly from the already too large SBBN value, y_Li 4.9 ± 1.1 ([Li]_P = 2.69_-0.11^+0.09).

4.6. Other Non-Standard Models

Although the parameterization of BBN in terms of S and _e explored in the previous sections encompasses a large set of non-standard models of cosmology and particle physics, it by no means describes all interesting extensions of the standard model. As already mentioned, there is a class of models where BBN proceeds normally but a second epoch of early universe nucleosynthesis is initiated by the late decay of a massive particle [40]. Despite the fact that such models have many more free parameters, such as the mass, abundance, and lifetime of the decaying particle, the constraints imposed by the observationally inferred relic abundances of D, ³He, ⁴He, and ⁷Li are sufficiently strong to challenge them (see, e.g., Ellis, Olive & Vangioni [40]).

There are other models which cannot be simply described by the {_B, S, _e} parameter set. In most cases they introduce several free parameters in addition to the baryon density parameter. Since there are only four nuclides whose relic abundances are reasonably constrained, the leverage of BBN on these models may be limited in some cases. A case in point is the class of models where the universe is inhomogeneous at BBN (IBBN); see the recent article by Lara [44] and the extensive references to earlier work therein. In IBBN the geometry of the inhomogeneities (spheres, cylinders, ...) is important, as are the scales of the imhomogeneities and their amplitudes (density contrasts). Nonetheless, even with all these adjustable parameters, except when they take on values indistinguishable from SBBN, IBBN models predict an excess of lithium (even more of an excess than for SBBN). This is inevitable since in IBBN ⁷Li is overproduced in the low nucleon density regions and ⁷Be is overproduced in the high density regions (see the multi-valued lithium abundance curve in Fig. 1).

⁶ By charge neutrality the charged lepton excess is equal to the proton excess which constitutes 0.6 87% of the baryon excess. Therefore, any significant lepton asymmetry (_e >> _B) must be hidden in the unobserved relic neutrinos. Back.