The first predictions of the anisotropy of the cosmic microwave background
(CMB) were published shortly after the CMB was discovered by
Penzias & Wilson
(1965).
Sachs & Wolfe (1967)
calculated the anisotropies due to
gravitational potential fluctuations produced by density perturbations
(Figure 1.1).
Because the density perturbations are given by the second derivative
of the gravitational potential fluctuation in Poisson's equation, the
Sachs-Wolfe effect dominates the temperature fluctuations at large
scales or low spherical harmonic index
. Sachs & Wolfe predicted
T / T
10-2 at large
scales. This prediction, which failed by a factor of 103, is
based on correct physics but incorrect input assumptions: prior to the
discovery of the CMB no one knew how uniform the Universe was on
large scales.
 |
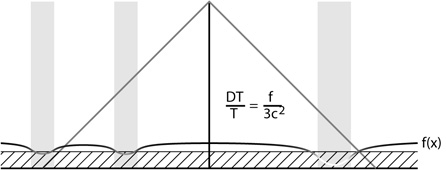Figure 1.1. Sachs & Wolfe (1967) predicted that density enhancements would be cold spots in the CMB, as shown in this conformal spacetime diagram. |
Silk (1968)
computed the density perturbations needed at the recombination epoch at
z
103 in order to produce galaxies, and predicted
T / T
3 ×
10-4 on arcminute scales.
Silk (1967)
calculated the damping of waves that were partially
optically thick during recombination. This process, known as "Silk
damping," greatly reduces the CMB anisotropy for small angular scales.
Observations by Conklin (1969) and then Henry (1971) showed that there was a dipole anisotropy in the CMB corresponding to the motion of the Solar System with respect to the average velocity of the observable Universe. There is a discussion of the dipole observations and their interpretation in Peebles (1971) that is still valid today, except that what was then a "tentative" dipole is now known to better than 1% accuracy, after a string of improved measurements starting with Corey & Wilkinson (1976) and ending with the COBE DMR (Bennett et al. 1996).
Peebles & Yu (1970)
calculated the baryonic oscillations resulting
from interactions between photons and hydrogen in the early Universe,
and also independently introduced the Harrison-Zel'dovich spectrum
(Harrison 1970;
Zel'dovich 1972).
Pebbles & Yu predicted
T / T
1.5 ×
10-4 on 1' scales and
T / T
1.7 ×
10-3 on 7' scales.
Wilson & Silk (1981)
further developed the theory of photon
and matter interaction by scattering and gravity, and predicted
T / T
= 100 µK for a single subtracted experiment
with a 7° throw and with a 7° beam like COBE.
Of course, when COBE was launched in 1989 it actually
observed a much smaller anisotropy.
These early predictions of a large anisotropy were greatly modified
by the addition of dark matter to the recipe for the cosmos.
Observational upper limits on small-scale anisotropies had
reached T /
T < 4 × 10-5 on 1.'5 scales
(Uson & Wilkinson
1982),
which was considerably less than
the predictions from universes with just baryons and photons.
Peebles (1982)
computed the anisotropy expected in a universe "dominated
by massive, weakly interacting particles" - in other words cold
dark matter (CDM), although this paper predated the use of "cold
dark matter."
Bond & Efstathiou
(1987)
calculated the correlation function of the CMB anisotropy,
C(
), and also the
angular power spectrum,
C, in the
CDM cosmology. This paper contains one of the first plots showing
( + 1)C vs.
, with peaks originally
called the "Doppler" peaks but more properly called
"acoustic peaks."
This paper solved the Boltzmann equation describing the evolution
of the photon distribution functions. Several authors developed
these "Boltzmann codes," but the calculation of the angular power
spectrum up to high was
very slow. These codes described the conversion of inhomogeneity at the
last-scattering surface into anisotropy on the observed sky by
a set of differential equations evolving the coefficients of
a Legendre polynomial expansion of the radiation intensity.
Since the Universe is almost completely transparent after recombination,
a ray-tracing approach is much more efficient.
This great step in efficiency was implemented in the CMBFAST code by
Seljak & Zaldarriaga
(1996).
Hu & Dodelson (2002)
give a recent review of CMB anisotropies,
which includes a very good tutorial on the theory of
T / T.