


A simple analysis of cosmological perturbations can be obtained from a consideration of the Newtonian approximation to a homogeneous and isotropic universe. Consider a test particle at radius R from an arbitrary center. Because the model is homogeneous the choice of center does not matter. The evolution of the velocity of the test particle is given by the energy equation
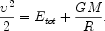 |
(1.1) |
If the total energy Etot is positive, the Universe
will expand forever since M, the mass (plus energy) enclosed
within R, is positive, G is positive, and R is
positive. In the absence of a cosmological constant or "dark
energy," the expansion of the Universe will stop, leading to a
recollapse if Etot is negative. But this simple
connection between Etot and
the fate of the Universe is broken in the presence of a vacuum energy
density. The mass M is proportional to R3
because the Universe is homogeneous and the Hubble velocity
 is given by
is given by
 = HR.
Thus Etot
= HR.
Thus Etot
 R2.
R2.
We can find the total energy by plugging in the velocity
 0 =
H0 R0 and the density
0 =
H0 R0 and the density
 0
in the Universe now. This gives
0
in the Universe now. This gives
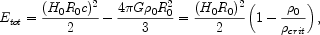 |
(1.2) |
with the critical density at time t0 being
 crit
= 3 H02 /
(8
crit
= 3 H02 /
(8 G).
We define the ratio of density to critical density as
G).
We define the ratio of density to critical density as
 =
=
 /
/
 crit.
This
crit.
This  includes all
forms of matter and energy.
includes all
forms of matter and energy.
 m will
be used to refer to the matter density.
m will
be used to refer to the matter density.
From Equation 1.1 we can compute the time variation of
 . Let
. Let
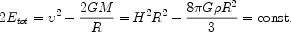 |
(1.3) |
If we divide this equation by 8 G
G
 R2/3 we get
R2/3 we get
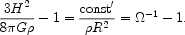 |
(1.4) |
Thus  -1
- 1
-1
- 1  (
( R2)-1.
When
R2)-1.
When  declines
with expansion at a rate faster than R-2
then the deviation of
declines
with expansion at a rate faster than R-2
then the deviation of
 from unity grows
with expansion. This is the situation during the matter-dominated epoch with
from unity grows
with expansion. This is the situation during the matter-dominated epoch with

 R-3, so
R-3, so
 -1 - 1
-1 - 1
 R. During
the radiation-dominated epoch
R. During
the radiation-dominated epoch

 R-4, so
R-4, so
 -1 - 1
-1 - 1
 R2.
For
R2.
For  0 to
be within 0.9 and 1.1,
0 to
be within 0.9 and 1.1,
 needed
to be between 0.999 and 1.001 at the epoch of recombination,
and within 10-15 of unity during nucleosynthesis.
This fine-tuning problem is an aspect of the "flatness-oldness"
problem in cosmology.
needed
to be between 0.999 and 1.001 at the epoch of recombination,
and within 10-15 of unity during nucleosynthesis.
This fine-tuning problem is an aspect of the "flatness-oldness"
problem in cosmology.
Inflation produces such a huge expansion that quantum fluctuations on the
microscopic scale can grow to be larger than the observable Universe.
These perturbations can be the seeds of structure formation and also will
create the anisotropies seen by COBE for spherical harmonic indices

 2. For perturbations that
are larger than ~ cs t
(or ~ cs / H) we can ignore pressure gradients,
since pressure gradients produce sound waves that are not able to cross
the perturbation in a Hubble time. In the absence of pressure gradients,
the density perturbation will evolve in the same way that a homogeneous
universe does, and we can use the equation
2. For perturbations that
are larger than ~ cs t
(or ~ cs / H) we can ignore pressure gradients,
since pressure gradients produce sound waves that are not able to cross
the perturbation in a Hubble time. In the absence of pressure gradients,
the density perturbation will evolve in the same way that a homogeneous
universe does, and we can use the equation
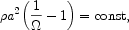 |
(1.5) |
the assumption that 
 1 for early times,
and
1 for early times,
and 
 <<
<<
 as indicated
by the smallness of the
as indicated
by the smallness of the
 T's
seen by COBE, to derive
T's
seen by COBE, to derive
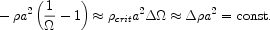 |
(1.6) |
Hence,
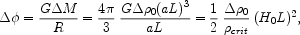 |
(1.7) |
where L is the comoving size of the perturbation. This is independent of the scale factor, so it does not change due to the expansion of the Universe.
During inflation
(Guth 2003),
the Universe is approximately in a steady state with constant
H. Thus, the magnitude of

 for
perturbations with physical
scale c/H will be the same for all times during the
inflationary epoch. But since this constant physical scale is aL,
and the scale factor a
changes by more than 30 orders of magnitude during inflation, this means
that the magnitude of
for
perturbations with physical
scale c/H will be the same for all times during the
inflationary epoch. But since this constant physical scale is aL,
and the scale factor a
changes by more than 30 orders of magnitude during inflation, this means
that the magnitude of

 will be the same
over 30 decades of comoving scale L. Thus, we get a strong
prediction that
will be the same
over 30 decades of comoving scale L. Thus, we get a strong
prediction that 
 will be the same on all observable scales from c /
H0 down to
the scale that is no longer always larger than the sound speed horizon.
This means that
will be the same on all observable scales from c /
H0 down to
the scale that is no longer always larger than the sound speed horizon.
This means that
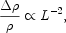 |
(1.8) |
so the Universe becomes extremely homogeneous on large scales even though it is quite inhomogeneous on small scales.
This behavior of

 being
independent of scale is called
equal power on all scales. It was originally predicted by
Harrison (1970),
Zel'dovich (1972),
and Peebles & Yu
(1970)
based on a very simple argument:
there is no scale length provided by the early Universe, and thus the
perturbations should be scale-free - a power law. Therefore
being
independent of scale is called
equal power on all scales. It was originally predicted by
Harrison (1970),
Zel'dovich (1972),
and Peebles & Yu
(1970)
based on a very simple argument:
there is no scale length provided by the early Universe, and thus the
perturbations should be scale-free - a power law. Therefore


 Lm.
The gravitational potential divided by c2 is a
component of the metric, and if it gets comparable to unity then wild
things happen. If m < 0
then
Lm.
The gravitational potential divided by c2 is a
component of the metric, and if it gets comparable to unity then wild
things happen. If m < 0
then 
 gets large for small L, and many black holes would form.
But we observe that this did not happen.
Therefore m
gets large for small L, and many black holes would form.
But we observe that this did not happen.
Therefore m  0. But
if m > 0 then
0. But
if m > 0 then

 gets large on
large scales, and the Universe would be grossly inhomogeneous.
But we observe that this is not the case, so m
gets large on
large scales, and the Universe would be grossly inhomogeneous.
But we observe that this is not the case, so m
 0. Combining both results requires that m = 0, which is a
scale-invariant perturbation
power spectrum. This particular power-law power spectrum is called the
Harrison-Zel'dovich spectrum.
It was expected that the primordial perturbations
should follow a Harrison-Zel'dovich spectrum because all other answers were
wrong, but the inflationary scenario provides a good mechanism for producing
a Harrison-Zel'dovich spectrum.
0. Combining both results requires that m = 0, which is a
scale-invariant perturbation
power spectrum. This particular power-law power spectrum is called the
Harrison-Zel'dovich spectrum.
It was expected that the primordial perturbations
should follow a Harrison-Zel'dovich spectrum because all other answers were
wrong, but the inflationary scenario provides a good mechanism for producing
a Harrison-Zel'dovich spectrum.
Sachs & Wolfe (1967) show that a gravitational potential perturbation produces an anisotropy of the CMB with magnitude
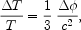 |
(1.9) |
where 
 is evaluated at
the intersection of the line-of-sight
and the surface of last scattering (or recombination at z
is evaluated at
the intersection of the line-of-sight
and the surface of last scattering (or recombination at z
 1100).
The (1/3) factor arises because clocks run faster by a factor (1 +
1100).
The (1/3) factor arises because clocks run faster by a factor (1 +
 /
c2)
in a gravitational potential, and we can consider the expansion of the
Universe to be a clock. Since the scale factor is varying as a
/
c2)
in a gravitational potential, and we can consider the expansion of the
Universe to be a clock. Since the scale factor is varying as a
 t2/3 at recombination, the faster expansion leads to a
decreased temperature by
t2/3 at recombination, the faster expansion leads to a
decreased temperature by
 T / T
= -(2/3)
T / T
= -(2/3)
 /
c2, which, when added to the
normal gravitational redshift
/
c2, which, when added to the
normal gravitational redshift
 T / T
=
T / T
= 
 /
c2 yields the (1/3) factor above.
This is an illustration of the "gauge" problem in calculating
perturbations in general relativity.
The expected variation of the density contrast as the square of the
scale factor for scales larger than the horizon in the radiation-dominated
epoch is only obtained after allowance is made for the
effect of the potential on the time.
For a plane wave with wavenumber k we have -k2
/
c2 yields the (1/3) factor above.
This is an illustration of the "gauge" problem in calculating
perturbations in general relativity.
The expected variation of the density contrast as the square of the
scale factor for scales larger than the horizon in the radiation-dominated
epoch is only obtained after allowance is made for the
effect of the potential on the time.
For a plane wave with wavenumber k we have -k2

 = 4
= 4 G
G

 , or
, or
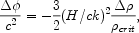 |
(1.10) |
so when 

 crit
at recombination, the Sachs-Wolfe
effect exceeds the physical temperature fluctuation
crit
at recombination, the Sachs-Wolfe
effect exceeds the physical temperature fluctuation
 T / T
= (1/4)
T / T
= (1/4)
 /
/
 by a factor
of 2(H / ck)2 if fluctuations are adiabatic
(all component number densities varying by the same factor).
by a factor
of 2(H / ck)2 if fluctuations are adiabatic
(all component number densities varying by the same factor).
In addition to the physical temperature fluctuation and the gravitational potential fluctuation, there is a Doppler shift term. When the baryon fluid has a density contrast given by
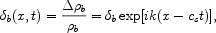 |
(1.11) |
where cs is the sound speed, then
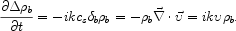 |
(1.12) |
As a result the velocity perturbation is given by
 =
-cs
=
-cs b.
But the sound speed is given by cs =
(
b.
But the sound speed is given by cs =
( P /
P /

 )1/2
= [(4/3)
)1/2
= [(4/3)
 c2 /
(3
c2 /
(3 b
+ 4
b
+ 4
 )]1/2
)]1/2
 c / 31/2,
since
c / 31/2,
since 
 >
>  b
at recombination (z = 1100).
But the photon density is only slightly higher than the baryon density
at recombination so the sound speed is about 20% smaller than
c / 31/2.
The Doppler shift term in the anisotropy is given by
b
at recombination (z = 1100).
But the photon density is only slightly higher than the baryon density
at recombination so the sound speed is about 20% smaller than
c / 31/2.
The Doppler shift term in the anisotropy is given by
 T / T
=
T / T
=  / c,
as expected. This results in
/ c,
as expected. This results in
 T / T
slightly less than
T / T
slightly less than
 b /
31/2, which is nearly
31/2 larger than the physical temperature fluctuation given
by
b /
31/2, which is nearly
31/2 larger than the physical temperature fluctuation given
by  T /
T =
T /
T =  b
/ 3.
b
/ 3.
These plane-wave calculations need to be projected onto the sphere that is
the intersection of our past light cone and the hypersurface corresponding
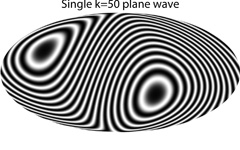
to the time of recombination. Figure 1.2 shows a
plane
wave on these surfaces. The scalar density and potential perturbations
produce a different pattern on the observed sky than the vector velocity
perturbation. Figure 1.3 shows these patterns on
the sky for a plane wave with k RLS = 50, where
RLS is the radius of
the last-scattering surface. The contribution of the velocity term is
multiplied by cos , and
since the RMS of this over the
sphere is (1/3)1/2, the RMS contribution of the velocity term
almost equals the RMS contribution from the density term
since the speed of sound is almost c/31/2.
, and
since the RMS of this over the
sphere is (1/3)1/2, the RMS contribution of the velocity term
almost equals the RMS contribution from the density term
since the speed of sound is almost c/31/2.
 |
 |
Figure 1.2. A plane wave on the last-scattering hypersurface. Right: The spherical intersection with our past light cone is shown. |
|
 |
 |
Figure 1.3. Left: The scalar density and potential perturbation. Right: The vector velocity perturbation. |
|
The anisotropy is usually expanded in spherical harmonics:
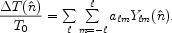 |
(1.13) |
Because the Universe is approximately isotropic the probability densities
for all the different m's at a given
 are identical. Furthermore,
the expected value of
are identical. Furthermore,
the expected value of
 T(
T(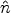 )
is obviously zero, and thus the expected values of the
a
)
is obviously zero, and thus the expected values of the
a m's
is zero. But the variance of the
a
m's
is zero. But the variance of the
a m's
is a measurable function of
m's
is a measurable function of  ,
defined as
,
defined as
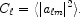 |
(1.14) |
Note that in this normalization
C and
a
and
a m
are dimensionless. The harmonic index
m
are dimensionless. The harmonic index
 associated with an angular
scale
associated with an angular
scale  is
given by
is
given by 
 180° /
180° /  , but the
total number of spherical
harmonics contributing to the anisotropy power at angular scale
, but the
total number of spherical
harmonics contributing to the anisotropy power at angular scale
 is given by
is given by 


 times
2
times
2 + 1. Thus to have
equal power on all scales one needs to have approximately
C
+ 1. Thus to have
equal power on all scales one needs to have approximately
C

 -2. Given that
the square of the angular momentum operator is actually
-2. Given that
the square of the angular momentum operator is actually
 (
( + 1), it is not surprising that
the actual angular power spectrum of the CMB predicted by "equal
power on all scales" is
+ 1), it is not surprising that
the actual angular power spectrum of the CMB predicted by "equal
power on all scales" is
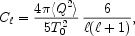 |
(1.15) |
where < Q2 > or
Q2rms-PS is the expected variance of the
 = 2 component of the sky,
which must be divided by T02 because
the a
= 2 component of the sky,
which must be divided by T02 because
the a m's are defined to be dimensionless. The
"4
m's are defined to be dimensionless. The
"4 " term
arises because the mean of
|Y
" term
arises because the mean of
|Y m|2 is 1 /
(4
m|2 is 1 /
(4 ), so the
|a
), so the
|a m|2's must be
4
m|2's must be
4 times larger to
compensate. Finally, the quadrupole has 5 components, while
C
times larger to
compensate. Finally, the quadrupole has 5 components, while
C is the
variance of a single component, giving the "5" in the
denominator. The COBE DMR experiment
determined (< Q2 >)1/2 = 18
µK, and that the
C
is the
variance of a single component, giving the "5" in the
denominator. The COBE DMR experiment
determined (< Q2 >)1/2 = 18
µK, and that the
C 's from
's from
 = 2 to
= 2 to
 = 20 were consistent with
Equation 1.15.
= 20 were consistent with
Equation 1.15.
The other common way of describing the anisotropy is in terms of
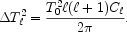 |
(1.16) |
Note these definitions give
 T22 = 2.4 < Q2 >.
Therefore, the COBE normalized Harrison-Zel'dovich spectrum has
T22 = 2.4 < Q2 >.
Therefore, the COBE normalized Harrison-Zel'dovich spectrum has
 T
T 2 = 2.4 × 182 = 778
µK2
for
2 = 2.4 × 182 = 778
µK2
for 
 20.
20.
It is important to realize that the relationship between the wavenumber
k and the spherical harmonic index
 is not a simple
is not a simple
 = k
RLS. Figure 1.3 shows that while
= k
RLS. Figure 1.3 shows that while
 = k
RLS at the "equator" the poles have lower
= k
RLS at the "equator" the poles have lower
 . In fact, if µ =
cos
. In fact, if µ =
cos , where
, where
 is the angle between
the wave vector and the line-of-sight, then the "local
is the angle between
the wave vector and the line-of-sight, then the "local
 " is
given by k RLS (1 -
µ2)1/2. The average of this over
the sphere is <
" is
given by k RLS (1 -
µ2)1/2. The average of this over
the sphere is <  > =
(
> =
( / 4) k
RLS.
For the velocity term the power goes to zero when µ = 0 on
the equator, so the average
/ 4) k
RLS.
For the velocity term the power goes to zero when µ = 0 on
the equator, so the average  is smaller, <
is smaller, <  > =
(3
> =
(3 / 16) k
RLS, and the distribution of
power over
/ 16) k
RLS, and the distribution of
power over  lacks the sharp
cusp at
lacks the sharp
cusp at  = k
RLS.
As a result the velocity term, while contributing about 60% as much to the
RMS anisotropy as the density term, does not contribute this
much to the peak structure in the angular power spectrum.
Thus the old nomenclature of "Doppler" peaks was not
appropriate, and the new usage of "acoustic" peaks is more
correct. Figure 1.4 shows the angular power spectrum
from single k skies for both the density and velocity terms for
several values of k, and a graph of the variance-weighted mean
= k
RLS.
As a result the velocity term, while contributing about 60% as much to the
RMS anisotropy as the density term, does not contribute this
much to the peak structure in the angular power spectrum.
Thus the old nomenclature of "Doppler" peaks was not
appropriate, and the new usage of "acoustic" peaks is more
correct. Figure 1.4 shows the angular power spectrum
from single k skies for both the density and velocity terms for
several values of k, and a graph of the variance-weighted mean
 vs. kRLS. These curves were computed numerically but
have the expected forms given by the spherical Bessel function
j
vs. kRLS. These curves were computed numerically but
have the expected forms given by the spherical Bessel function
j for the
density term and
j
for the
density term and
j ' for the
velocity term.
' for the
velocity term.
Seljak (1994) considered a simple model in which the photons and baryons are locked together before recombination, and completely noninteracting after recombination. Thus the opacity went from infinity to zero instantaneously. Prior to recombination there were two fluids, the photon-baryon fluid and the CDM fluid, which interacted only gravitationally. The baryon-photon fluid has a sound speed of about c / 31/2 while the dark matter fluid has a sound speed of zero. Figure 1.5 shows a conformal spacetime diagrams with a traveling wave in the baryon-photon fluid and the stationary wave in the CDM. The CDM dominates the potential, so the large-scale structure (LSS) forms in the potential wells defined by the CDM.
In Seljak's simple two-fluid model, there are five variables to
follow: the density contrast in the CDM and baryons,
 c and
c and
 b, the
velocities of these fluids
b, the
velocities of these fluids
 c
and
c
and  b,
and the potential
b,
and the potential
 . The photon
density contrast is
(4/3)
. The photon
density contrast is
(4/3) b. In
Figure 1.6
the density contrasts are plotted vs. the scale factor for several
values of the wavenumber. To make this plot the density contrasts
were adjusted for the effect of the potential on the time, with
b. In
Figure 1.6
the density contrasts are plotted vs. the scale factor for several
values of the wavenumber. To make this plot the density contrasts
were adjusted for the effect of the potential on the time, with
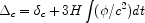 |
(1.17) |
and
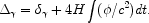 |
(1.18) |
Remembering that
 is negative
when
is negative
when  is positive, the
two terms on the right-hand side of the above equations cancel almost
entirely at early times, leaving a small residual growing like
a2 prior to aeq, the scale factor
when the matter density and the radiation
density were equal. Thus these adjusted density contrasts evolve like
is positive, the
two terms on the right-hand side of the above equations cancel almost
entirely at early times, leaving a small residual growing like
a2 prior to aeq, the scale factor
when the matter density and the radiation
density were equal. Thus these adjusted density contrasts evolve like
 -1-1 in
homogeneous universes.
-1-1 in
homogeneous universes.
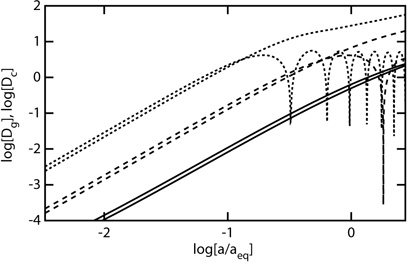 |
Figure 1.6. Density contrasts in the CDM
and the photons for wavenumbers
|
Figure 1.7 shows the potential that survives to recombination and produces LSS, the potential plus density effect on the CMB temperature, and the velocity of the baryons as function of wavenumber. Close scrutiny of the potential curve in the plot shows the baryonic wiggles in the LSS that may be detectable in the large redshift surveys by the 2dF and SDSS groups.
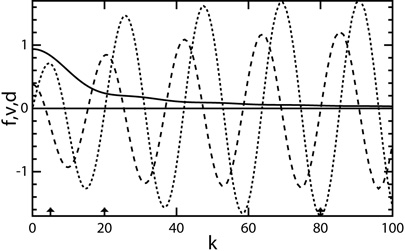 |
Figure 1.7. Density contrasts at
recombination as a function of
wavenumber |
A careful examination of the angular power spectrum allows several
cosmological parameters to be derived. The baryon to photon ratio
and the dark matter to baryon density ratio can both be derived from
the amplitudes of the first two acoustic peaks. Since the photon
density is known precisely, the peak amplitudes determine the baryon density
 b =
b =
 b
h2 and the cold dark matter
density
b
h2 and the cold dark matter
density  c =
c =
 CDM
h2. The matter density is given by
CDM
h2. The matter density is given by
 m =
m =
 b +
b +
 CDM.
The amplitude < Q2 >
and spectral index n of the primordial density perturbations
are also easily observed.
Finally the angular scale of the peaks depends on the ratio of the
angular size distance at recombination to the distance sound can travel
before recombination. Since the speed of sound is close to
c / 31/2, this sound travel distance is primarily
affected by the age
of the Universe at z = 1100. The age of the Universe goes like
t
CDM.
The amplitude < Q2 >
and spectral index n of the primordial density perturbations
are also easily observed.
Finally the angular scale of the peaks depends on the ratio of the
angular size distance at recombination to the distance sound can travel
before recombination. Since the speed of sound is close to
c / 31/2, this sound travel distance is primarily
affected by the age
of the Universe at z = 1100. The age of the Universe goes like
t 
 -1/2
-1/2

 m-1/2 h-1.
The angular size distance is proportional to h-1 as
well, so the Hubble constant cancels out. The angular size distance is
almost proportional to
m-1/2 h-1.
The angular size distance is proportional to h-1 as
well, so the Hubble constant cancels out. The angular size distance is
almost proportional to
 m-1/2, but this relation is
not quite exact. Figure 1.8 compares the angular
size distance to
m-1/2, but this relation is
not quite exact. Figure 1.8 compares the angular
size distance to  m-1/2. One sees that a peak position
that corresponds to
m-1/2. One sees that a peak position
that corresponds to
 tot =
0.95 if
tot =
0.95 if  m
= 0.2 can also be fit by
m
= 0.2 can also be fit by
 tot = 1.1
if
tot = 1.1
if  m =
1. Thus, to first order the peak position is a good measure of
m =
1. Thus, to first order the peak position is a good measure of
 tot.
tot.
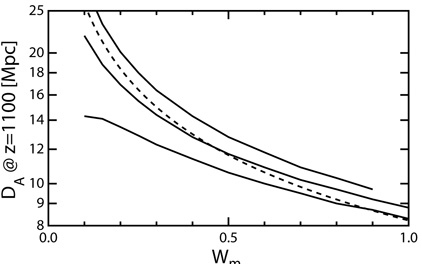 |
Figure 1.8. The angular size distance vs.
|
The CMBFAST code by
Seljak & Zaldarriaga
(1996)
provides the ability to quickly compute the angular power spectrum
C .
Typically CMBFAST runs in about 1 minute for a given set of cosmological
parameters. However, two different groups have developed even
faster methods to evaluate
C
.
Typically CMBFAST runs in about 1 minute for a given set of cosmological
parameters. However, two different groups have developed even
faster methods to evaluate
C .
Kaplinghat, Knox, &
Skordis (2002)
have published the Davis Anisotropy Shortcut (DASh), with
code available for download. This program interpolates among precomputed
C
.
Kaplinghat, Knox, &
Skordis (2002)
have published the Davis Anisotropy Shortcut (DASh), with
code available for download. This program interpolates among precomputed
C 's.
Kosowsky, Milosavljevic,
& Jiminez (2002)
discuss combinations of the parameters that produce simple changes
in the power spectrum, and also allow accurate and fast
interpolation between
C
's.
Kosowsky, Milosavljevic,
& Jiminez (2002)
discuss combinations of the parameters that produce simple changes
in the power spectrum, and also allow accurate and fast
interpolation between
C 's. These
shortcuts allow the computation of a
C
's. These
shortcuts allow the computation of a
C from
model parameters in about 1 second. This allows the rapid computation of the
likelihood of a given data set D for a set of model
parameters M, L(D|M). When computing the
likelihood for high signal-to-noise ratio observations of a small area
of the sky, biases due to the non-Gaussian shape of the likelihood are
common. This can be avoided using the offset log-normal form for the
likelihood L(C
from
model parameters in about 1 second. This allows the rapid computation of the
likelihood of a given data set D for a set of model
parameters M, L(D|M). When computing the
likelihood for high signal-to-noise ratio observations of a small area
of the sky, biases due to the non-Gaussian shape of the likelihood are
common. This can be avoided using the offset log-normal form for the
likelihood L(C ) advocated by
Bond, Jaffe, & Knox
(2000).
) advocated by
Bond, Jaffe, & Knox
(2000).
| Experiment |  b (') b (') |
100(  ) / ) /
 |
100( dT) / dT dT) / dT |
| COBE | 420.0 | -0.3 | ... |
| ARCHEOPS | 15.0 | -0.2 | 2.7 |
| BOOMERanG | 12.9 | 10.5 | -7.6 |
| MAXIMA | 10.0 | -0.9 | 0.2 |
| DASI | 5.0 | -0.4 | 0.7 |
| VSA | 3.0 | -0.5 | -1.7 |
| CBI | 1.5 | -1.1 | -0.2 |
The likelihood is a probability distribution over the data,
so  L(D|M) dD = 1 for any M. It is not a
probability distribution over the models, so one should
never attempt to evaluate
L(D|M) dD = 1 for any M. It is not a
probability distribution over the models, so one should
never attempt to evaluate
 L
dM. For example, one could consider the likelihood as a function
of the model parameters H0 in km s-1
Mpc-1 and
L
dM. For example, one could consider the likelihood as a function
of the model parameters H0 in km s-1
Mpc-1 and
 m for
flat
m for
flat  CDM models,
or one could use the parameters t0 in seconds and
CDM models,
or one could use the parameters t0 in seconds and
 m. For
any (H0,
m. For
any (H0,
 m) there is a
corresponding (t0,
m) there is a
corresponding (t0,
 m) that
makes exactly the same predictions, and therefore gives the same
likelihood. But the integral of the likelihood over dt0
d
m) that
makes exactly the same predictions, and therefore gives the same
likelihood. But the integral of the likelihood over dt0
d m
will be much larger than the integral of the likelihood over
dH0
d
m
will be much larger than the integral of the likelihood over
dH0
d m
just because of the Jacobian of the transformation between the different
parameter sets.
m
just because of the Jacobian of the transformation between the different
parameter sets.
Wright (1994) gave the example of determining the primordial power spectrum power-law index n, P(k) = A(k / k0)n. Marginalizing over the amplitude by integrating the likelihood over A gives very different results for different values of k0. Thus, it is very unfortunate that Hu & Dodelson (2002) still accept integration over the likelihood.
Instead of integrating over the likelihood one needs to define the a posteriori probability of the models pf(M) based on an a priori distribution pi(M) and Bayes' theorem:
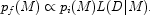 |
(1.19) |
It is allowable to integrate pf over the space of models because the prior will transform when changing variables so as to keep the integral invariant.
In the modeling reported here, the a priori distribution is chosen
to be uniform in
 b,
b,
 c, n,
c, n,
 V,
V,
 tot,
and zri. In doing the fits, the model
C
tot,
and zri. In doing the fits, the model
C 's are
adjusted by a factor of exp[a + b
's are
adjusted by a factor of exp[a + b
 (
( + 1)] before comparison with the
data. Here a is a calibration adjustment, and b is a beam
size correction that assumes a Gaussian beam. For COBE, a
is the overall amplitude scaling parameter instead of a calibration
correction. Marginalization over the calibration and beam size corrections
for each experiment, and the overall spectral amplitude, is done by
maximizing the likelihood, not by integrating the likelihood.
Table 1.1 gives these beam and calibration
corrections for each experiments. All of these corrections are less than
the quoted uncertainties for these experiments.
BOOMERanG stands out in the table for having honestly reported its
uncertainties: ± 11% for the beam size and ± 10% for the gain.
The likelihood is given by
+ 1)] before comparison with the
data. Here a is a calibration adjustment, and b is a beam
size correction that assumes a Gaussian beam. For COBE, a
is the overall amplitude scaling parameter instead of a calibration
correction. Marginalization over the calibration and beam size corrections
for each experiment, and the overall spectral amplitude, is done by
maximizing the likelihood, not by integrating the likelihood.
Table 1.1 gives these beam and calibration
corrections for each experiments. All of these corrections are less than
the quoted uncertainties for these experiments.
BOOMERanG stands out in the table for having honestly reported its
uncertainties: ± 11% for the beam size and ± 10% for the gain.
The likelihood is given by
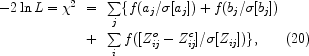 |
(1.20) |
where j indexes over experiments, i indexes over points
within each experiment, Z =
ln(C + N
+ N ) in
the offset log normal approach of
Bond et al. (2000),
and N
) in
the offset log normal approach of
Bond et al. (2000),
and N is
the noise bias. Since for COBE a is the overall
normalization, σ(a) is set
to infinity for this term to eliminate it from the likelihood.
The function f(x) is x2 for small
|x| but switches to
4(|x| - 1) when |x| > 2. This downweighs outliers in the
data. Most of the experiments have double tabulated their data. I have used
both the even and odd points in my fits, but I have multiplied the
is
the noise bias. Since for COBE a is the overall
normalization, σ(a) is set
to infinity for this term to eliminate it from the likelihood.
The function f(x) is x2 for small
|x| but switches to
4(|x| - 1) when |x| > 2. This downweighs outliers in the
data. Most of the experiments have double tabulated their data. I have used
both the even and odd points in my fits, but I have multiplied the
 's by 21/2 to
compensate. Thus, I expect to get
's by 21/2 to
compensate. Thus, I expect to get
 2 per
degree of freedom close to 0.5 but should have the correct sensitivity to
cosmic parameters.
2 per
degree of freedom close to 0.5 but should have the correct sensitivity to
cosmic parameters.
| Parameter | Mean |  |
Units |
 b b |
0.0206 | 0.0020 | |
 c c |
0.1343 | 0.0221 | |
 V V |
0.3947 | 0.2083 | |
 k k |
-0.0506 | 0.0560 | |
| zri | 7.58 | 3.97 | |
| n | 0.9409 | 0.0379 | |
| H0 | 51.78 | 12.26 | km s-1 Mpc-1 |
| t0 | 15.34 | 1.60 | Gyr |
 |
0.2600 | 0.0498 | |
The scientific results such as the mean values and the
covariance matrix of the parameters can be
determined by integrations over parameter space
weighted by pf.
Table 1.2 shows the mean and
standard deviation of the parameters determined by
integrating over the a posteriori probability distribution of
the models. The evaluation of integrals
over multi-dimensional spaces can require a large
number of function evaluations when the dimensionality
of the model space is large, so a Monte Carlo approach can be used.
To achieve an accuracy of
 (
( ) in
a Monte Carlo integration requires
) in
a Monte Carlo integration requires
 (
( -2)
function evaluations, while achieving the same
accuracy with a gridding approach requires
-2)
function evaluations, while achieving the same
accuracy with a gridding approach requires
 (
( -n/2)
evaluations when second-order methods are
applied on each axis. The Monte Carlo approach is more
efficient for more than four dimensions.
When the CMB data get better, the likelihood gets more
and more sharply peaked as a function of the parameters,
so a Gaussian approximation to L(M) becomes more
accurate, and concerns about banana-shaped confidence
intervals and long tails in the likelihood are reduced.
The Monte Carlo Markov Chain (MCMC)
approach using the Metropolis-Hastings algorithm to
generate models drawn from pf is a relatively
fast way to evaluate these integrals
(Lewis & Bridle 2002).
In the MCMC, a "trial" set of parameters
is sampled from the proposal density
pt(P';P),
where P is the current location in parameter space,
and P' is the new location. Then the trial location is
accepted with a probability given by
-n/2)
evaluations when second-order methods are
applied on each axis. The Monte Carlo approach is more
efficient for more than four dimensions.
When the CMB data get better, the likelihood gets more
and more sharply peaked as a function of the parameters,
so a Gaussian approximation to L(M) becomes more
accurate, and concerns about banana-shaped confidence
intervals and long tails in the likelihood are reduced.
The Monte Carlo Markov Chain (MCMC)
approach using the Metropolis-Hastings algorithm to
generate models drawn from pf is a relatively
fast way to evaluate these integrals
(Lewis & Bridle 2002).
In the MCMC, a "trial" set of parameters
is sampled from the proposal density
pt(P';P),
where P is the current location in parameter space,
and P' is the new location. Then the trial location is
accepted with a probability given by
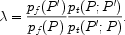 |
(1.21) |
When a trial is accepted the Markov chain one sets P = P'. This algorithm guarantees that the accepted points in parameter space are sampled from the a posteriori probability distribution.
The most common choice for the proposal density is
one that depends only on the parameter change P'- P.
If the proposal density is a symmetric function then the
ratio pt(P;P') /
ptP';P) = 1 and
 is
then just the ratio of a posteriori probabilities. But the most
efficient choice for the proposal density is
pf(P) which is not
a function of the parameter change, because
this choice makes
is
then just the ratio of a posteriori probabilities. But the most
efficient choice for the proposal density is
pf(P) which is not
a function of the parameter change, because
this choice makes  = 1
and all trials are accepted.
However, if one knew how to sample models from pf, why
waste time calculating the likelihoods?
= 1
and all trials are accepted.
However, if one knew how to sample models from pf, why
waste time calculating the likelihoods?
Just plotting the cloud of points
from MCMC gives a useful indication of the
allowable parameter ranges that are consistent with
the data. I have done some MCMC calculations using the DASh
(Kaplinghat et al. 2002)
to find the
C 's.
I found DASh to be user unfriendly and too likely to terminate
instead of reporting an error for out-of-bounds parameter sets,
but it was fast.
Figure 1.9 shows the range
of baryon and CDM densities consistent with the CMB data set from
COBE
(Bennett et al. 1996),
ARCHEOPS
(Amblard 2003),
BOOMERanG
(Netterfield et al. 2002),
MAXIMA
(Lee et al. 2001),
DASI
(Halverson et al. 2002),
VSA
(Scott et al. 2003),
and CBI
(Pearson et al. 2003),
and the range of matter and vacuum densities consistent with these
data. The Hubble constant is strongly correlated with
position on this diagram. Figure 1.10 shows the
distribution of t0 for models consistent with this
pre-WMAP CMB data set. The relative uncertainty in
t0
is much smaller than the relative uncertainty in H0
because the low-H0 models have low vacuum energy
density (
's.
I found DASh to be user unfriendly and too likely to terminate
instead of reporting an error for out-of-bounds parameter sets,
but it was fast.
Figure 1.9 shows the range
of baryon and CDM densities consistent with the CMB data set from
COBE
(Bennett et al. 1996),
ARCHEOPS
(Amblard 2003),
BOOMERanG
(Netterfield et al. 2002),
MAXIMA
(Lee et al. 2001),
DASI
(Halverson et al. 2002),
VSA
(Scott et al. 2003),
and CBI
(Pearson et al. 2003),
and the range of matter and vacuum densities consistent with these
data. The Hubble constant is strongly correlated with
position on this diagram. Figure 1.10 shows the
distribution of t0 for models consistent with this
pre-WMAP CMB data set. The relative uncertainty in
t0
is much smaller than the relative uncertainty in H0
because the low-H0 models have low vacuum energy
density ( V),
and thus low values of the product H0
t0. The CMB
data are giving a reasonable value for t0 without using
information on the distances or ages of objects, which is
an interesting confirmation of the Big Bang model.
V),
and thus low values of the product H0
t0. The CMB
data are giving a reasonable value for t0 without using
information on the distances or ages of objects, which is
an interesting confirmation of the Big Bang model.
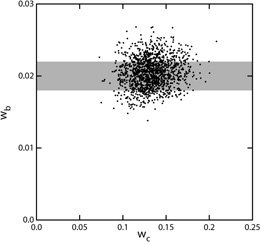 |
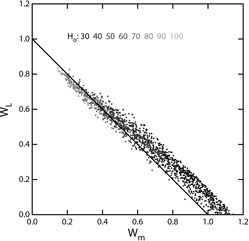 |
Figure 1.9. Left: Clouds
of models drawn from the a posteriori distribution
based on the CMB data set as of 19 November 2002. The gray band shows
the Big Bang nucleosynthesis determination of
|
|
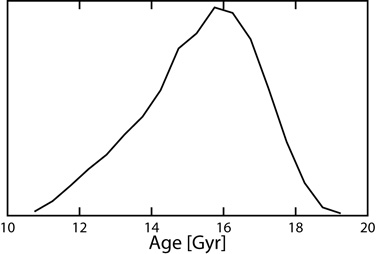 |
Figure 1.10. Distribution of the age of the Universe based only on the pre-WMAP CMB data. |
Peacock & Dodds (1994)
define a shape parameter for the observed LSS power spectrum,
 =
=
 m h
exp(-2
m h
exp(-2 b).
There are other slightly different definitions of
b).
There are other slightly different definitions of
 in use, but
this will be used consistently here. Peacock & Dodds determine
in use, but
this will be used consistently here. Peacock & Dodds determine
 = 0.255 ±
0.017 + 0.32(n-1-1).
The CMB data specify n, so the slope correction in the last term is
only 0.020 ± 0.013. Hence, the LSS power spectrum wants
= 0.255 ±
0.017 + 0.32(n-1-1).
The CMB data specify n, so the slope correction in the last term is
only 0.020 ± 0.013. Hence, the LSS power spectrum wants
 = 0.275 ±
0.02. The models based only on the pre-WMAP CMB
data give the distribution in
= 0.275 ±
0.02. The models based only on the pre-WMAP CMB
data give the distribution in
 shown in
Figure 1.11,
which is clearly consistent with the LSS data.
shown in
Figure 1.11,
which is clearly consistent with the LSS data.
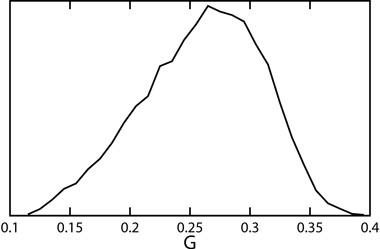 |
Figure 1.11. Distribution of the LSS power
spectrum shape parameter
|
Two examples of flat
( tot =
1) models with equal power on all
scales (n = 1), plotted on the pre-WMAP data set, are
shown in Figure 1.12.
Both these models are acceptable fits, but the
tot =
1) models with equal power on all
scales (n = 1), plotted on the pre-WMAP data set, are
shown in Figure 1.12.
Both these models are acceptable fits, but the
 CDM
model is somewhat favored based on the positions of the
peaks. The rise in
C
CDM
model is somewhat favored based on the positions of the
peaks. The rise in
C at low
at low  for the
for the
 CDM model is
caused by the
late integrated Sachs-Wolfe effect, which is due to the changing
potential that occurs for z < 1 in this model.
The potential changes because the density contrast stops
growing when
CDM model is
caused by the
late integrated Sachs-Wolfe effect, which is due to the changing
potential that occurs for z < 1 in this model.
The potential changes because the density contrast stops
growing when  dominates while the Universe continues to expand at an accelerating
rate. The potential change during a photon's passage through a structure
produces a temperature change given by
dominates while the Universe continues to expand at an accelerating
rate. The potential change during a photon's passage through a structure
produces a temperature change given by
 T / T
= 2
T / T
= 2
 /
c2 (Fig. 1.13).
The factor of 2 is the same factor of 2 that enters into
the gravitational deflection of starlight by the Sun.
The effect should be correlated with LSS that we can see at z
/
c2 (Fig. 1.13).
The factor of 2 is the same factor of 2 that enters into
the gravitational deflection of starlight by the Sun.
The effect should be correlated with LSS that we can see at z
 0.6.
Boughn & Crittenden
(2003)
have looked for this correlation using COBE maps compared
to radio source count maps from the NVSS, and
Boughn, Crittenden, &
Koehrsen (2002)
have looked at the correlation of COBE and
the X-ray background. As of now the
correlation has not been seen, which is an area of concern for
0.6.
Boughn & Crittenden
(2003)
have looked for this correlation using COBE maps compared
to radio source count maps from the NVSS, and
Boughn, Crittenden, &
Koehrsen (2002)
have looked at the correlation of COBE and
the X-ray background. As of now the
correlation has not been seen, which is an area of concern for
 CDM, since the
(non)correlation implies
CDM, since the
(non)correlation implies

 = 0
± 0.33 with roughly Gaussian errors.
This correlation should arise primarily from
redshifts near z = 0.6, as shown in
Figure 1.14.
The coming availability of LSS maps based on deep all-sky infrared surveys
(Maller 2003)
should allow a better search for this correlation.
= 0
± 0.33 with roughly Gaussian errors.
This correlation should arise primarily from
redshifts near z = 0.6, as shown in
Figure 1.14.
The coming availability of LSS maps based on deep all-sky infrared surveys
(Maller 2003)
should allow a better search for this correlation.
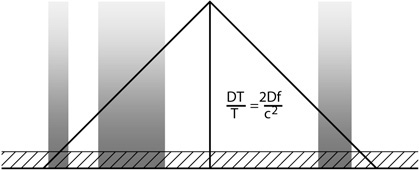 |
Figure 1.13. Fading potentials cause large-scale anisotropy correlated with LSS due to the late integrated Sachs-Wolfe effect. |
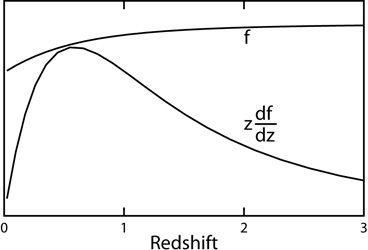 |
Figure 1.14. Change of potential
vs. redshift in a
|
In addition to the late integrated Sachs-Wolfe effect from
 , reionization
should also enhance
C
, reionization
should also enhance
C at low
at low
 , as would an admixture of
tensor waves. Since
, as would an admixture of
tensor waves. Since
 ,
,
 ri and T /
S all increase
C
ri and T /
S all increase
C at low
at low
 , and this
increase is not seen, one has an upper limit on a weighted sum of all
these parameters. If
, and this
increase is not seen, one has an upper limit on a weighted sum of all
these parameters. If
 is finally
detected by the correlation between improved CMB and LSS maps, or if
a substantial
is finally
detected by the correlation between improved CMB and LSS maps, or if
a substantial  ri,
such as the
ri,
such as the  = 0.1 predicted
by Cen (2003),
is detected by the correlation between the E-mode polarization and
the anisotropy
(Zaldarriaga 2003),
then one gets a greatly strengthened limit on tensor waves.
= 0.1 predicted
by Cen (2003),
is detected by the correlation between the E-mode polarization and
the anisotropy
(Zaldarriaga 2003),
then one gets a greatly strengthened limit on tensor waves.