2. SINGLE-FLUID MHD-SHOCKS

Shock waves are usually considered as a sharp transition between a macroscopic supersonic (and super-Alfvénic) upstream flow (state 1) and slowed down to a subsonic velocity downstream flow (state 2), providing a mass flow j_n through the shock surface. It is assumed that a gas particle (or an elementary macroscopic fluid cell) is at any instant of time in the local thermodynamic equilibrium state corresponding to the instantaneous values of the macroscopic parameters. The Maxwellian distribution of all species is ensured after a few molecular (or Coulomb) collisions have occurred. The macroscopic parameters characterising the state of the gas, such as density, specific internal energy, or temperature, change slowly in comparison with the rates of the relaxation processes leading to thermodynamic equilibrium. We consider here a single-fluid plasma model assuming complete electron-ion relaxation. Under these conditions, in a frame moving with the shock front, with the matter flux across the shock surface j_n 0, the conservation laws for mass (in non-relativistic flows), momentum and energy can be written as follows:

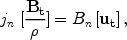(1)

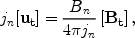(2)

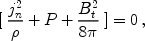(3)

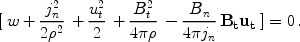(4)

Here U = (u_n, u_t) is the bulk velocity, w = + P / is the gas enthalpy, , P, are the internal gas energy, pressure and density respectively. The subscripts n and t are used for the normal and transverse components respectively. We used the standard notations [A] = A₂ - A₁ for the jump of a function A between the downstream and upstream regions. In the MHD case the relations equivalent to Eq. 1-4 were obtained by de Hoffmann & Teller (1950). The equations are valid in the case of a magnetic field frozen-into moving plasma, where E = -U / c × B. A specific feature of MHD shock waves is the so-called coplanarity theorem (e.g. Landau & Lifshitz 1984) saying that the upstream and downstream magnetic fields B₁ and B₂ and the shock normal all lie in the same plane as it is illustrated in Fig. 1. It is important to note that if B_n 0 there is an especial reference frame where local velocity U and magnetic field B are parallel both in the upstream and downstream, providing E = 0.

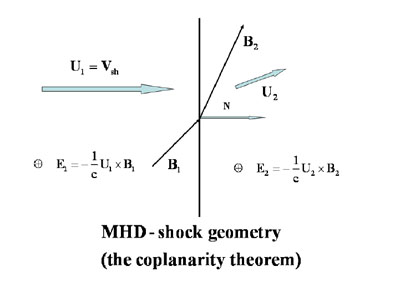Figure 1. A sketch illustrating the coplanarity theorem for a plane ideal MHD-shock. The upstream and downstream bulk velocities U1 and U2, magnetic fields B1 and B2 and the shock normal N all lie in the same plane. The shock is at rest in the reference frame where also ut1 = 0. The shock is of infinitesimal width in the sketch. Simulated structure of the transition region of a collisionless shock is shown in Fig. 2 and Fig. 3 where its finite width is apparent.

From Eq. 1-4 one may obtain a generalised Rankine-Hugoniot (RH) adiabat

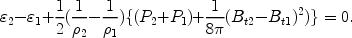(5)

The RH adiabat connects the macroscopic parameters downstream of the flow once the upstream state is known. In a parallel shock (B_t = 0)

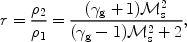(6)

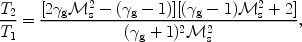(7)

where _g is the gas adiabatic exponent. We restrict ourselves here to a fast mode shock where c_s1 < u₁, and v_a2 < u₂ < c_s2, for v_a1 < c_s1. The phase velocity v_a2 is the Alfvén velocity in the downstream, c_s1, c_s2 are the sound speeds in the upstream and downstream respectively. We define here the shock Mach numbers as _s = v_sh / c_s1 and _a = v_sh / v_a1.

In the case of a perpendicular shock (B_n = 0) the compression ratio is

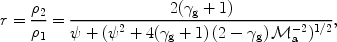(8)

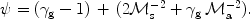In a single fluid strong shock with _s >> 1 and _a >> 1 one gets

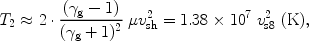(9)

for any magnetic field inclination (e.g. Draine & McKee 1993). The mass per particle µ was assumed to be [1.4/2.3] m_H and v_s8 is the shock velocity in 10⁸ cm s^-1.

The RH adiabat does not depend on the exact nature of the dissipation mechanisms that provide the transition between the states 1 and 2. It assumes a single-fluid motion in regular electromagnetic fields. However, the dissipative effects control the thickness of the shock transition layer. In the case of a weak shock of Mach number _s - 1 << 1 the thickness is large enough, allowing a macroscopic hydrodynamical description of the fluid inside the shock transition layer (e.g. Landau & Lifshitz 1984). The gas shock width in collisional hydrodynamics without magnetic fields is given by

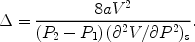(10)

Following Landau & Lifshitz (1959) the gas shock width in Eq. 10 can be expressed through the viscosities and , and thermal conductivity , since

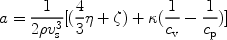Here c_v and c_p are specific heats at constant volume and at constant pressure respectively. Extrapolating Eq. 10 to a shock of finite strength where P₂ - P₁ ~ P₂, one may show that the gas shock width is of the order of the mean free path .

It is instructive to note that the entropy is non-monotonic inside the finite width of a weak gas shock (_s - 1) << 1 and the total RH jump of the entropy s across the shock is of the third order in (_s - 1):

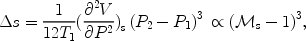(11)

while the density, temperature and pressure jumps are (_s - 1) (Landau & Lifshitz 1959).

In plasma shocks the shock structure is more complex because of a relatively slow electron-ion temperature relaxation. Such a shock consists of an ion viscous jump and an electron-ion thermal relaxation zone. In the case of plasma shocks the structure of the ion viscous jump is similar to the single fluid shock width structure discussed above and can be studied accounting for the entropy of an isothermal electron fluid. The shock ion viscous jump has a width of the order of the ion mean free path. The scattering length (the mean free path to /2 deflection) _p of a proton of velocity v₇ (measured in 100 km s^-1) due to binary Coulomb collisions with plasma protons of density n (measured in cm^-3) can be estimated as _p 7 × 10¹⁴ v₇⁴ n^-1 cm (Spitzer 1962). After the reionisation (z < 6) the Coulomb mean free path in the WHIM of overdensity is _p 3.5 × 10²¹ v₇^{4 -1} (1 + z)^-3 (_b h² / 0.02)^-1 cm. Here and below _b is the baryon density parameter. The mean free path due to Coulomb collisions is typically some orders of magnitude smaller than that for the charge-exchange collisions in the WHIM after reionisation. The ion-electron thermal relaxation occurs on scales about _e × (m_p / Z m_e)^1/2. Since _e ~ _p, the width of the relaxation zone is substantially larger than the scale size of the ion viscous jump. The application of the single fluid shock model Eq. 1-4 to electron-ion plasmas assumes full ion-electron temperature relaxation over the shock width. For a discussion of the relaxation processes see e.g. Bykov et al. 2008 - Chapter 8, this volume, and references therein.

In a rarefied hot cosmic plasma the Coulomb collisions are not sufficient to provide the viscous dissipation of the incoming flow, and collective effects due to the plasma flow instabilities play a major role, providing the collisionless shocks, as it is directly observed in the heliosphere. The observed structure of supernova remnants (e.g. Weisskopf & Hughes 2006) is consistent with that expected if their forward shocks are collisionless. Moreover, the non-thermal synchrotron emission seen in radio and X-rays is rather a strong argument for high energy particle acceleration by the shock that definitely favours its collisionless nature. That allows us to suggest that cosmological shocks in a rarefied highly ionised plasma (after the reionisation epoch) are likely to be collisionless. There are yet very few observational studies of cosmological shocks (e.g. Markevitch & Vikhlinin 2007). We review some basic principles of collisionless shock physics in the next section.