Since the discovery of the solar wind in the early 1960's it has been realised that the rapid rise time of magnetic storms observed in the Earth suggested very thin collisionless shocks created by solar flares (see for a discussion Sagdeev 1966, Kennel et al. 1985). The thickness of a viscous jump in a strong collisional shock is of the order of a mean free path (see e.g. Zel'dovich & Raizer 1967). The Coulomb collision mean free path in the tenuous solar wind plasma is comparable to the Sun-Earth distance, and thus the magnetic storm rising time due to standard collisional shocks would exceed the observed time by orders of magnitude.
There are very specific features of collisionless plasma shocks (Sagdeev 1966). Shocks in dense enough plasma with frequent Coulomb collisions evolve very fast to Maxwellian particle distributions with very few particles at high energies. On the contrary, in collisionless plasma shocks, a small minority of particles could gain a disproportionate share of the energy and become non-Maxwellian. Collisionless shocks enable acceleration of a small fraction of the particles to very high energies. Moreover, the accelerated particles could carry away a substantial amount of the kinetic energy of the plasma flow dissipated at the shock. The energetic particles can penetrate far into the shock upstream gas, to create an extended shock precursor. The cold gas in the shock upstream is decelerated and pre-heated by the energetic particle and MHD-wave pressure on a scale larger than a mean free path of an energetic particle. This occurs not only at the bow shock of the Earth at moderately low energies, but also in astrophysical shocks at highly relativistic energies (e.g. Russell 2005).
A direct study of collisionless shock waves in a laboratory is an extremely difficult task. Most of the experimental data on collisionless shock physics are coming from space experiments. There are direct observational data on the shock wave structure in the interplanetary medium with clear evidence for ion and electron acceleration by the shocks (e.g. Tsurutani & Lin 1985, Russell 2005).
Computer simulations of the full structure of collisionless shock waves describe the kinetics of multi-species particle flows and magneto-hydrodynamic (MHD) waves in the strongly-coupled system. The problem is multi-scale. It requires a simultaneous treatment of both "microscopic" structure of the subshock at the thermal ion gyroradii scale where the injection process is thought to occur, and an extended "macroscopic" shock precursor due to energetic particles. The precursor scale is typically more than 109 times the microscopic scale of the subshock transition region.
Energetic particles could be an essential component in the WHIM and clusters of galaxies. Nonthermal particle acceleration at shocks is expected to be an efficient process at different evolutional stages of clusters. Being the governing process of the supernova remnant collisionless shock formation, nonlinear wave-particle interactions are responsible for both shock heating and compression of the thermal gas, as well as for creation of an energetic particle population.
3.1. Micro processes in collisionless shocks
In the strong enough collisionless shocks (typically with a Mach number above a few) resistivity cannot provide energy dissipation fast enough to create a standard shock transition (e.g. Kennel et al. 1985) on a microscopic scale. Ion instabilities are important in such shocks that are called supercritical.
At the microscopic scale the front of a supercritical shock wave
is a transition region occupied by magnetic field fluctuations of
an amplitude 
B /
B ~ 1 and characteristic frequencies of
about the ion gyro-frequency. Generation of the fluctuations is
due to instabilities in the interpenetrating multi-flow ion
movements. The width of the transition region of a quasi-parallel
shock wave reaches a few hundred ion inertial lengths defined as
li = c /
pi
2.3 ×
107 n-0.5 cm.
Here pi is
the ion plasma frequency and n is the
ionised ambient gas number density measured in cm-3. The ion
inertial length in the WHIM can be estimated as li
5.1 ×
1010
-1/2 (1 +
z)-3/2
(
b
h2 / 0.02)-1/2 cm, providing
the width of the collisionless shock transition region is smaller
by many orders of magnitude than the Coulomb mean free path (that
is in the kiloparsec range).
The transition region of a quasi-perpendicular shock is somewhat narrower. The wave generation effects at the microscopic scale have been studied in some detail with hybrid code simulations (e.g. Quest 1988). The large-amplitude magnetic field fluctuations in the shock transition region were directly measured in the interplanetary medium (see e.g. Kan et al. 1991).
There are a few ways to simulate numerically the kinetics of the collisionless plasma phenomena. The most comprehensive study of the collisionless shock structure can be performed with the particle-in-cell (PIC) method where all the plasma components are considered as discrete particles in self-consistent fields. The PIC method allows one to resolve electron scale lengths and frequencies, but on the other hand it requires considerable computer resource. A serious constraint on PIC and other plasma particle simulations of collisionless shocks is that they must be done fully in three spatial dimensions (3D). Jones et al. (1998) have proved that PIC simulations with one or more ignorable dimensions artificially confine particles to field lines and particularly eliminate cross-field diffusion. The effect is especially important for simulations of a creation of a superthermal particle population. All three box dimensions must be involved in these simulations. Exact modelling of electron kinetics in collisionless shocks require PIC simulations (e.g. Hoshino & Shimada 2002, Schmitz et al. 2002). On the other hand, the bulk of the energy of a collisionless shock is carried by the ions and velocity relaxation processes are typically longer than the ion gyro-periods. Thus, though the basic shock physics evolve on ion spatial and temporal scales, the electron kinetic description requires fine resolution at electron scales.
A fairly good description of low-frequency processes of the ion dynamics in the shock transition layer can be achieved with hybrid codes (e.g. Winske & Omidi 1996 and references therein). Hybrid code modelling, which interprets protons as particles and electrons as an inertialess liquid, has made it possible to describe some important features of the (sub)shock waves at the microscopic scale of some hundred times the ion inertial length (e.g. Quest 1988, Lembege et al. 2004, Burgess et al. 2005).
A typical initialisation of a shock in the hybrid code simulations is to inject a relatively cold ion beam (say at the right-hand boundary) and to put a particle reflecting wall at the left-hand boundary of a simulation box. In that case the shock is moving, and the available simulation time is limited, given the finite size of the box. The limited simulation time and the particle statistics per cell are challenging the direct modelling of the origin and evolution of the energetic non-thermal particle population in a shock. To increase the statistics the macro-particle splitting method is used (see e.g. Quest 1992, Giacalone & Ellison 2000).
In Fig. 2 we show the structure of the magnetic
field in a quasi-perpendicular shock (inclination angle
θBn
80°) simulated with a hybrid code for the upstream plasma
parameter 
~ 1. The parameter
=
a2
/ s2,
characterises the ratio of the thermal and
magnetic pressures. The shock is propagating along the x-axis
from the left to the right. The magnetic field is in the x - z
plane. The system is periodic in the y-dimension. Phase densities
of protons vx - x, vy -
x, vz - x are shown in
Fig. 3 in the reference frame where the particle
reflecting wall (at far left) is at rest while the shock front is
moving. The incoming plasma beam in the simulation was composed of
protons (90%), alpha particles (9.9%) and a dynamically
insignificant fraction of oxygen ions (O VII).
 |
 |
Figure 2. Hybrid simulated magnetic fields of a quasi-perpendicular shock (80° inclination). The shock propagates along the x-axis, while the initial regular magnetic field is in the x-z plane. We show the By and Bz dependence on x in the left and right panels respectively. |
|
 |
 |
 |
Figure 3. Hybrid simulated proton phase density in a quasi-perpendicular shock (80° inclination). The shock is moving from left to right in the reference frame where the particle reflecting wall is at rest. The figures show the proton phase densities in vx - x, vy - x and vz - x projections from top to bottom respectively. |
In most of the cases non-relativistic shocks simulated with
different hybrid codes had the upstream plasma parameter
~ 1. In some cosmological shocks, for example in hot X-ray
clusters, plasma parameter
could be
~ 100 (see
Bykov et al. 2008
- Chapter 8, this volume). The nature of collisionless
shocks in the hot low magnetised plasmas could be different from
that in case of
~
1. While the processes of shock
formation in the high beta plasmas still require a careful study,
there are two experimental studies establishing the existence of the
collisionless shocks for that case. A collisionless shock in a
laboratory experiment with a laser-produced ablating plasma of
~ 300 was
found to have a thickness about 10
c / pe,
that is orders of magnitude less than the
Coulomb mean free path of both ions and electrons in that system (see
Bell et al. 1988).
In space plasma the terrestrial bow shock under high beta conditions was
observed with the ISEE 1 and ISEE 2 spacecraft by
Farris et
al. (1992).
These measurements
were compared with and found to be in agreement with the predicted
values of the Rankine-Hugoniot relations using the simple adiabatic
approximation and a ratio of specific heats, gamma, of 5/3. Large
magnetic field and density fluctuations were observed, but average
downstream plasma conditions well away from the shock were
relatively steady, near the predicted Rankine-Hugoniot values. The
magnetic disturbances persisted well downstream and a hot, dense ion
beam was detected leaking from the downstream region of the shock.
3.2. Heating of ions in collisionless shocks
The heating processes in collisionless shocks are non-trivial. The
irreversible transformation of a part of the kinetic energy
of the ordered bulk motion of the upstream flow into the energy of
the random motions of plasma particles in the downstream flow in
collisional shocks is due to Coulomb or atomic particle
collisions. In collisional non-radiative shocks without slowly
relaxing molecular components, the standard single-fluid RH
relations are applicable just after a few collisional lengths. The
standard single-component shock model predicts a particle
temperature kT = (3/16) mvsh2
for 
= 5/3.
The particle distributions in the collisionless shocks are not Maxwellian. Thus, instead of the standard equilibrium temperature the appropriate moments of the particle distribution function characterising the width of randomised velocity distributions are used. Moreover, the particle velocity distributions are typically anisotropic. It is clearly seen in hybrid simulated proton phase density: in Fig. 3 the velocity distribution widths are different for different projections. One can see in Fig. 3 that a fraction of the incoming ions is reflected by the shock magnetic field jump providing multiple inter-penetrating flows of gyrating ions. Then the field fluctuations randomise the ion phases producing a "coarse-grained" distribution characterised by an effective temperature estimated as the second moment of the velocity distribution.
An analysis of interplanetary collisionless shock observations made
with Advanced Composition Explorer by
Korreck et
al. (2007)
indicated that quasi-perpendicular shocks are heating ions more
efficiently than quasi-parallel shocks. It was also found that
effective temperatures of different ions are not necessarily
proportional to ion mass, but also depend on the shock inclination
angle and plasma parameter
. The
widths of the collisionless
shocks are extremely narrow (below the astronomical unit) and thus,
the observed temperatures would depend on the temperature
equilibration processes (both Coulomb and collective) that we will
discuss elsewhere (e.g.
Bykov et
al. 2008
- Chapter 8, this volume). The temperature equilibration of different
plasma constituents in the WHIM can be studied with spatially resolved
spectroscopic observations and thus is a good test for shock models.
3.3. Heating of electrons in collisionless shocks
Electron kinetics in collisionless shocks are different from those of
ions. Since most of the observable emission comes from the
electrons, they require a careful study. Shocks transfer a fraction
of the bulk kinetic energy of the ion flow into large amplitude
nonlinear magnetic fluctuations on a short scale of the transition
region (see Fig. 2). It is important that the
thermal electron velocities in the ambient medium are higher than the shock
speed for a shock Mach number
s
< (mp / me)1/2,
allowing for a nearly-isotropic angular distribution of the
electrons. Non-resonant interactions of these electrons with the
large-amplitude turbulent fluctuations in the shock transition
region could result in collisionless heating and pre-acceleration
of the electrons
(Bykov & Uvarov
1999).
In Fig. 4 a
simulated electron distribution (p2 N(z,
p)) is shown as a
function of the dimensionless electron momentum p /
(2me T1)1/2,
where T1 is the initial electron temperature in the far
upstream (z 
-
).
The solid curves are the simulated electron distribution functions at
the left boundary (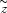
= 0) of the transition region clearly seen in
Fig. 2, and at the end of the region
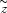( = 1). Dotted lines
are the Maxwellian distribution fits allowing to estimate the effective
electron temperatures Teff measured relative to
T1. Note that Teff = 1.2 at
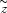= 0 because of the
electron diffusivity effect. One may also clearly see the appearance of
non-thermal tails indicating a Fermi type acceleration. It is worth
noting that the presence of large-amplitude waves in the shock
transition region erodes many of the differences between quasi-parallel
and perpendicular shocks, making the electron injection mechanism in
that model to be similar for these shocks.
 |
Figure 4. Electron distribution function
simulated in the model of electron heating by strong ion gyroradii
scale magnetic fluctuations in a collisionless shock by
Bykov & Uvarov
(1999).
The left panel is for |
The analysis of observational data on both interplanetary and supernova shocks by Ghavamian et al. (2007) indicates that theelectron heating efficiency i.e. Te / Ti is a declining function of the shock velocity. These authors discussed a model of electron heating with a constant level of electron heating over a wide range of shock speeds (see also Fig. 4 in Bykov & Uvarov 1999e), while the ion heating is an increasing function of shock velocity .
3.4. Gas heating and entropy production in weak internal shocks
Heating/acceleration efficiency with weak and moderate strength MHD
shocks can be estimated by calculating the energy dissipation rate
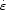h of a directed gas motion per unit
area of a weak shock. Defining
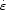h = vsh
T
s, where
s is the
difference of the entropies (per unit mass) behind and ahead of the
shock front, one can evaluate the thermal gas heating as
 |
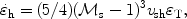(12) |
where 
t
is the gas internal energy per unit volume (cf. Eq. 11). The energy
transfer to the reflected nonthermal particles can be estimated from:
 |
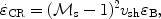(13) |
where B is
the magnetic energy density
(Bykov & Toptygin
1987).
From Eq. 12 and Eq. 13 one can see that the gas
heating is of third order in
(s -1) <<
1 (cf.
Landau &
Lifshitz 1959),
while the wave damping due to the particle
acceleration is of second order. Note that in the outer parts of
galaxy clusters one would typically expect
t >>
B.
However, the central regions of such a cluster could have
t
comparable to
B, as it
is the case in the Milky Way. Thus, the
weak shocks in the central regions could efficiently accelerate
nonthermal particles, reducing the heating of the gas. Particle
acceleration by an ensemble of large scale shocks in a cluster of
galaxies can create a population of non-thermal particles of
sizeable pressure. This may imply a non-steady evolution of
non-thermal pressure as modelled by
Bykov (2001).
= <(