2. X-RAY SPECTRA OF HOT TENUOUS PLASMA

The plasma of the ICM is very tenuous, with densities of 10^-5 to 10^-1 cm^-3 from the cluster outskirts to the densest regions of cool core clusters. This low plasma density makes the cluster X-ray spectra modeling simple and enables a very straightforward interpretation. Three fundamental emission processes involving electronic "transitions" contribute to the radiation: free-free or bremsstrahlung radiation caused by the deflection of an electron at close fly-by of an ion, free-bound or recombination radiation caused by the capture of an electron by an ion following ionization, and bound-bound or deexcitation radiation of an electron changing the quantum level in an ion. The first two processes give rise to continuum radiation and the latter to line radiation. An exception in bound-bound transitions is the radiative transition from the 2s to the 1s state, which is completely forbidden by angular momentum conservation, but can happen as very slow two-photon process. This "two-photon radiation" involves a distribution function of the branching ratio of the energies of the two electrons (Spitzer & Greenstein 1951) and thus gives rise to continuum radiation.

We note that all these radiative processes depend on the collision (or close fly-by) of an electron and an ion. Due to the very low density of the plasma all the ions excited by collisions have sufficient time for radiative deexcitation before a second deexciting collision occures. Thus contrary to laboratory plasmas, where slow transitions are "forbidden" and the corresponding excited states are much more rapidly deexcited by electronic collision, all "forbidden" transitions actually happen in the ICM plasma. This leads to a scenario where all exciting, recombining, and bremsstrahlung causing collisions lead to the radiation of a photon, which is referred to as the thin plasma radiation limit (or "coronal limit", as similar conditions prevail in the solar corona). The modeling of the thermal plasma spectrum is therefore a book keeping exercise of all the electron ion collisions rates and - in the case of several deexcitation channels - their branching ratios. These collision rates are in general a function of temperature (for thermal plasma) and the outcome is directly proportional to the electron density and the respective ion density. The shape of the resulting spectrum is therefore a function of the temperature and chemical composition and its normalization is directly proportional to the electron density and the ion density. The latter is true for the low plasma density limit that pertains in the ICM.

We further note that in general all photons so created leave the ICM plasma due to its low density. An exception is discussed in section 5.5.3 for the strongest lines in dense cluster cores. Thus no radiative transfer calculation is necessary for the interpretation of the X-ray spectra of the ICM. This means in particular that the spectrum we observe from a galaxy cluster provides an account of the entire ICM plasma, which is very different from e.g. the spectra of stars, that provide information on merely a very thin skin on their surface. This is another reason why cluster X-ray spectra are so informative and straightforward to interpret.

As the radiation contribution specific to an ion species is proportional to the density of this species in the plasma, the modeling of the overall spectrum also requires the knowledge of the chemical composition of the plasma and its ionization structure. For thermal equilibrium plasma, the ionization structure is characterized by the balance of the ionization and recombination rates for all the ionization steps of an element:

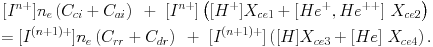(1)

Several processes contribute to the ionization and recombination rate. The ionization comprises direct electron impact ionization, C_ci, electron impact excitation into an auto-ionization state with subsequent auto-ionization, C_ai, and ionizing charge exchange with H⁺, He⁺, and He⁺⁺ with the rates X_ce1 and X_ce2, respectively. Direct ionization is the dominant process. Recombination rates include radiative recombination, C_rr, dielectronic recombination, C_dr, and electron capture charge exchange with H and He,with the rates X_ce3 and X_ce4. In the dielectronic recombination process the recombination collision complex is energetically stabilized by the excitation of a second bound electron which subsequently radiates the excess energy. This is a resonant process which exhibits a strong energy dependence which is most important for ions with many electrons (e.g. Fe ions). The ionization structure is calculated from the complete set of linear equations for all important ions and elements (e.g. Arnaud & Rothenflug 1985, Arnaud et al. 1992, Mazzotta et al. 1998). Fig. 2 shows for example the thermal equilibrium ionization structure of oxygen in the temperature range 10⁴ to 10⁸ K (Böhringer 1998).

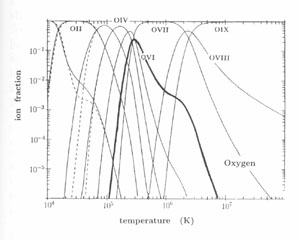Figure 2. Thermal equilibrium ionization structure of the oxygen ion family as a function of plasma temperature (Böhringer 1998).

The collision rates that lead to the emission of radiation are then all of the form:

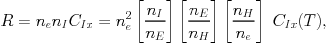(2)

where n_E, n_I, and n_H are the number densities of the elements, ions, and hydrogen nuclei, respectively, and C_Ix are the relevant collision rate coefficients for ion I. Consequently, [n_I / n_E] represents the fractional abundance of ionization stage I, [n_E / n_H] the relative elemental abundance, and [n_H / n_e] the Hydrogen nuclei to electron ratio, which is about 1.2. Thus all rates are proportional to the squared plasma density, n_e². The normalization of the spectrum is therefore determined from the emission measure, E, given by:

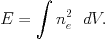(3)

We note that this definition of emission measure is not unique. It conforms to most definitions in text books, but the major public plasma radiation codes use the definition E = n_e n_H dV. The strategy of calculating the radiation spectrum of hot, thin plasma in thermal equilibrium is thus summarized in Fig. 3. The notion of thermal equilibrium involves a thermal Maxwellian equilibrium of the electrons and the thermal ionization equilibrium of the ions. A deviation of the temperature of the electrons and the ions will not affect the components of the radiation spectrum, but will be detected through thermal line broadening.

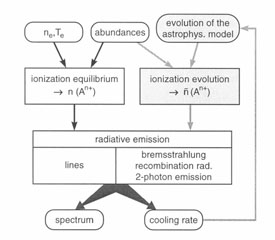Figure 3. Scheme of the calculation of the radiation spectrum and cooling function of a hot, tenuous plasma in thermal equilibrium. The shaded boxes include the situation of non-equilibrium ionization (from Böhringer 1998).

With a change of the temperature of the plasma the ionization structure is adjusted on the time scale of the inverse ionization and recombination rates and thus lags behind the temperature change. In certain cases this time lag is significant and has to be included in the modeling, as sketched in Fig. 3 by explicitly following the time evolution of the ionization structure. As an example, Fig. 4 shows the calculation of a passively cooling plasma starting at high temperature (Shapiro & Moore 1976) where the instantaneous ionization equilibrium assumption is compared to the full time dependent ionization structure calculations. We see that strong deviations occur at temperatures of the order of 10⁵ K, but no significant deviation from the ionization equilibrium calculations are observed above 10⁶ K, which is the temperature range in clusters. So far no observed X-ray spectrum of the ICM has required a non-ionization equilibrium treatment. Fig. 5 shows the contributions of continuum and line emission and the respective contributions of the most important elements (assuming solar abundances) to the total radiation power. The regime in which the recombination lags behind cooling can easily be identified with the temperature range where line radiation from the important, most abundant elements (particularly Fe) is strongly boosting the line cooling. We note that continuum bremsstrahlung with a temperature dependence of roughly T^1/2 is the dominant radiation process at ICM temperatures.

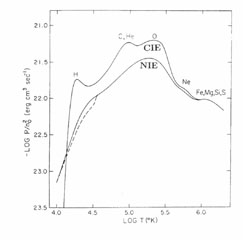Figure 4. Cooling coefficient of hot plasma as a function of the electron temperature (from Shapiro & Moore 1976). Two scenarios of the cooling of plasma from an initially hot phase of T ~ 107 K are compared. In the CIE (collisional ionization equilibrium) case the ionization structure is kept in full thermal equilibrium, in the NIE (non-ionization equilibrium) case on the contrary, the ionization structure passively follows the cooling plasma and recombination can lag behind the cooling. The latter implies higher ionization stages at the same temperature, that is less shell electrons and reduced line cooling.

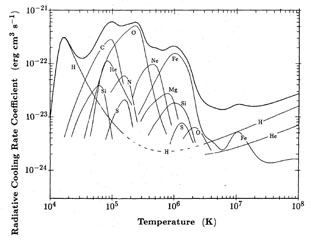Figure 5. Cooling rate of hot plasma as a function of the plasma temperature. The contribution to the cooling by the ions of different important abundant elements is indicated (Böhringer & Hensler 1989). Most of this contribution is in the form of line radiation, which is by far the dominant form of radiation in the temperature range from about 104 to 2 × 106 K. At higher temperatures over most of the regime of interest for the ICM the Bremsstrahlung contribution dominates.

Early modeling of the emission spectrum of hot, thin plasma include: Cox & Tucker (1969), Tucker & Koren (1971), Cox & Daltabuit (1971), Cox (1972), Shapiro & Moore (1976), Shapiro & Moore (1977), Kato (1976), Raymond & Smith (1977), Landini & Monsignori Fossi (1970), Landini & Monsignori Fossi (1990), Landini & Fossi (1991), Gaetz & Salpeter (1983), Raymond (1988), Masai (1984), Masai & Kato (1987), Böhringer & Hensler (1989), Schmutzler & Tscharnuter (1993), Sutherland & Dopita (1993), Brickhouse et al. (1995), Raymond & Brickhouse (1996). Now the two most frequently used plasma radiation codes are the MEKAL code (Gronenschild & Mewe 1978, Mewe & Gronenschild 1981, Mewe et al. 1985, Mewe 1990, Mewe 1991, Kaastra & Mewe 1994, Mewe et al. 1995) and the APEC code (Smith et al. 2001). While the older literature contains all the necessary information about the radiation codes including all the details of the rate calculations and much detail on the underlying physical processes, the modern codes are too complex to be easily described in the literature. Thus, unfortunately very little documentation about the new development of the radiation codes is available in written form after the mid 1990s.

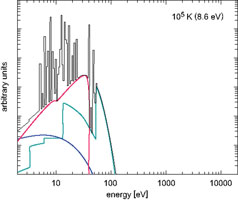
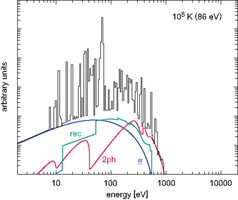
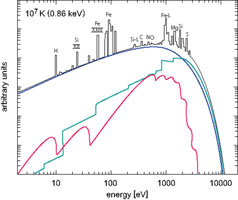
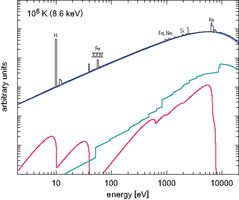
Fig. 6 shows typical spectra at temperatures of 10⁵, 10⁶, 10⁷, and 10⁸ K with solar element abundances, indicating the contribution by line radiation and the continuum emission from bremsstrahlung, recombination and two-photon transitions. We clearly see the increasing dominance of bremsstrahlung with increasing temperature, which reflects the fact that fewer ions retain electrons and the plasma is almost completely ionized at the higher temperatures.

Figure 6. X-ray spectra for solar abundance at different plasma temperatures. The continuum contributions from bremsstrahlung (blue), recombination radiation, characterized by the sharp ionization edges (green), and 2-photon radiation (red) are indicated. At the highest temperatures relevant for massive clusters of galaxies bremsstrahlung is the dominant radiation process (from the work described in Böhringer & Hensler (1989). The major emission lines in the panels for the higher temperatures relevant for galaxy clusters are designated by the elements from which they originate (The labels Fe-L ans Si-L refer to transitions into the L-shell in ions of Fe and Si, respectively, and two other lines with roman numbers carry the designation of the ions from which they originate involving transitions within the L-shells.