3.1. Determining the Direction of Motion
The kinematics of the BLR have been a long-standing problem. It has been known from the earliest days of AGN studies that the lines are very broad (for a review of the earliest literature see Seyfert 1943), but Doppler shifts only tell us the motion of gas along the line of sight. To know whether the gas is inflowing, outflowing, moving in random virialized orbits, or in more planar Keplerian orbits in a disc we need to know the line-of-sight velocity as a function of position relative to the black hole.
The discovery of narrow intrinsic absorption in NGC 4151 (Mayall 1934, Anderson & Kraft 1969) and of broad absorption lines (BALs) in PHL 5200 (Lynds 1967) proved that some gas was outflowing from AGNs. However, BALs commonly extend to velocities several times higher than those observed for the BLR in the same objects (see, for example, Turnshek et al. 1988), so it is not clear that there is necessarily any connection between BALs and BLRs. The case for an outflowing BLR was strengthened though when Blumenthal & Mathews (1975) and Baldwin (1975) showed that a radiatively-accelerated outflow could reproduce the observed line profiles well in some objects. However, Capriotti, Foltz, & Byard (1980) showed that other models could provide comparably good fits to broad-line profiles, and so demonstrated that fits to individual line profiles alone could not uniquely determine the kinematics.
More progress was made by comparing lines of differing ionizations.
Gaskell (1982)
discovered that high-ionization broad lines were blueshifted with respect to
low-ionization lines, and pointed out that this requires there to be
radial motions plus some source of opacity. This blueshifting
has now been widely confirmed.
Gaskell (1982)
suggested that the blueshifting could be the result of a
"disk-wind" model where the high-ionization lines arise in a wind
outflowing above the accretion disc.
Wilkes
& Carswell (1982)
pointed out a problem with any purely radial motion: the
profiles of C IV and Lyman
were observed to be
very similar, yet, for optically-thick clouds, Lyman
is emitted very
anisotropically. To satisfy this constraint the clouds either had to be
optically thin, or not moving purely radially.
Obviously the question of the direction of motion could be settled if it could be determined which gas was on which side of the black holes. The best way of doing this is through velocity-resolved reverberation mapping (Gaskell 1988). How this works is illustrated in Fig. 8. Surprisingly, velocity-resolved reverberation mapping results (Gaskell 1988, Koratkar & Gaskell 1989, Crenshaw & Blackwell 1990, Koratkar & Gaskell 1991a, Koratkar & Gaskell 1991b, Koratkar & Gaskell 1991c, Korista et al. 1995, Done & Krolik 1996, Ulrich & Horne 1996, Sergeev et al. 1999) strongly ruled out significant outflow of both high- and low-ionization lines (see example in Fig. 9).
 |
Figure 8. Velocity-resolved reverberation mapping. Because of light-travel-time effects, the gas on the near side of the AGN is seen to respond to continuum changes first. For the the hypothetical outflowing BLR illustrated here, the blue wing of a line would vary first. |
 |
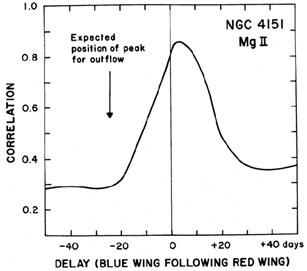Figure 9. The cross-correlation function for the blue and red wings of the Mg II line in NGC 4151 as a function of time delay. The predicted peak in the correlation function for pure outflow (blue wing varies first) is shown by the arrow. It can be seen instead that the strongest correlation is for near zero delay (what is expected for virialized or Keplerian motion), but with the red wind leading by a small but significant amount thus implying some net inflow. Figure from Gaskell (1988). |
Ruling out significant outflow of the BLR was important not just because of what it said about how AGNs work, but also because it meant that the BLR motions were gravitationally dominated. The BLR could thus be used for determining the masses of the central black holes. This permitted the first reverberation mapping determinations of black hole masses and Eddington ratios (Gaskell 1988, Koratkar & Gaskell 1989, Crenshaw & Blackwell 1990, Koratkar & Gaskell 1991a, Koratkar & Gaskell 1991b, Koratkar & Gaskell 1991c). 2 Note that while gravity dominates BLR motions, the simple fact that radiation pressure was at one time considered to be driving BLR motions (e.g., Blumenthal & Mathews 1975) should warn us that radiation pressure might not be negligible (Marconi et al. 2008).
While the velocity-resolved reverberation mapping results were good news for the new black-hole-mass-determination industry, they created a problem for the generally accepted "disk-wind" explanation of the blueshiftings of high-ionization lines. Disk-wind models are very theoretically appealing, and strong blueshiftings have been taken as signs of strong winds (e.g., Leighly & Moore 2004). However, at the same time, people working on black hole mass determinations were firmly believing that they were using virialized lines! This has almost caused AGN observers to suffer from multiple-personality disorder! 3 ,4
It is very difficult to finesse a disk-wind model to fit the velocity-resolved reverberation mapping constraint, all the more so since outflow was first excluded for the high-ionization C IV line (Gaskell 1988, Koratkar & Gaskell 1989, Crenshaw & Blackwell 1990, Koratkar & Gaskell 1991a, b, c). We believe, however, that there is a simple solution to the problem: the opacity needed to cause the blueshifting is not primarily absorption but scattering (Gaskell & Goosmann 2008). Electron scattering had in fact been considered in the late 1960s to be a significant source of line broadening in AGNs (Kaneko & Ohtani 1968, Weymann 1970, Mathis 1970), but the idea fell out of favor with the success of the Blumenthal & Mathews (1975) radiative acceleration model in fitting profiles. It has, however, long been well known (e.g., Edmonds 1950, Auer & van Blerkom 1972) that scattering off regions with a net radial motion produces line shifts. For an infalling scattering medium, photons gain energy. This is explained in Fig. 10. The process is similar to the well-known Fermi acceleration process. The effect of scattering off radially moving material in AGNs was considered by Kallman & Krolik (1986) and Ferrara & Pietrini (1993).
 |
Figure 10. Cartoon illustrating why scattered photons are blueshifted when scattered off a reflector which is approaching the source of photons. The person on the right sees her reflection (far left) in the mirror. If the mirror is approaching her, then the image is approaching her twice as quickly. |
As can be seen in Fig. 9, velocity-resolved reverberation mapping not only excludes outflow, but it also shows that there is a slight inflow. Initially this result only had ~ 90% confidence for any one line in one object, but it has been found repeatedly for many lines in many objects now and thus, as pointed out by Gaskell & Snedden (1997), the overall significance is high. Early examples included Gaskell (1988), Koratkar & Gaskell (1989), Crenshaw & Blackwell (1990), Koratkar & Gaskell (1991a, b, c), Korista et al. (1995), Done & Krolik (1996), Ulrich & Horne (1996). More recent examples can be found in Sergeev et al. (1999), Kollatschny (2003), Welsh et al. (2007), Doroshenko et al. (2008), Bentz et al. (2008), Denney et al. (2009a), Bentz et al. (2009c). Important independent evidence for inflow comes from high-resolution spectropolarimetry (e.g., Smith et al. 2005). The systematic change in polarization as a function of velocity across the Balmer lines requires a net inflow of a scattering region somewhat exterior to the Balmer lines. Polarization reverberation mapping (Gaskell et al. 2008a) can reveal the location of scattering regions.
We have used the STOKES Monte Carlo radiative transfer code (Goosmann & Gaskell 2007) 5 to model the effects on line profiles of scattering off an inflowing external medium. The two geometries considered are shown in Fig. 11. One is an infalling spherical distribution of scatterers and the other an infalling cylindrical distribution. In Fig. 12 we show a comparison of observed profiles of two low- and high- ionization lines in PKS 0304-392 with various models with. We adopted an infall velocity of ~ 1000 km s-1 based on velocity-dependent reverberation mapping, spectropolarimetry, and the observed mean blueshift (see Gaskell & Goosmann 2008 for details). It can be seen that both spherically and cylindrically symmetric models readily reproduce the blueshifting.
 |
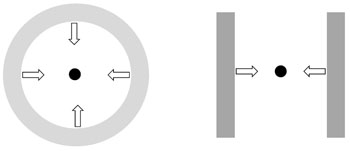Figure 11. Cross sections in a plane through the axis of symmetry of the two scattering region geometries modeled in Fig. 12. |
 |
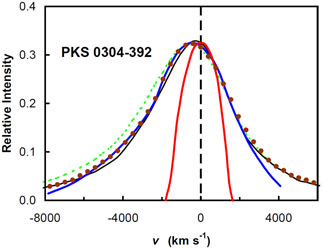Figure 12. Modelling the blueshifting of
high-ionization lines. The profiles of O I
|
An additional advantage of having significant scattering in the BLR is that it solves the "smoothness problem" for BLR line profiles (Capriotti, Foltz, & Byard 1981). The intrinsic line broadening in an individual BLR cloudlet is only of the order of the sound speed (~ 15 km s-1), yet the velocity broadening of the BLR as a whole is hundreds of times greater. This requires the number of clouds to be very high (Capriotti, Foltz, & Byard 1981, Atwood et al. 1982). The limit on the number of discrete clouds has now been pushed up to 108 (Arav et al. 1998, Dietrich et al. 1999). This constraint is relaxed if there is broadening by scattering.
3.2. The overall velocity field of the BLR
For a typical AGN, several independent lines of evidence (the blueshifting, velocity-resolved reverberation mapping, and spectropolarimetry) all point to the inflow velocity being of the order of ~ 1000 km s-1. As has been mentioned, velocity-resolved reverberation mapping (see, for example, Fig. 9) implies that the dominant motion is not radial, but Keplerian or random. The observed widths of broad lines are indeed several times higher than the inflow velocity, and, of course, the predominant motion for a flattened distribution must be Keplerian.
As is clear from Fig. 6 and 7, when we observe the BLR (i.e., in type-1 objects) we are always seeing it close to face-on. The Keplerian component of velocity must be reduced by sini, where i is the angle between the axis of rotational symmetry and the line of sight. The statistics of line profiles in the SDSS (La Mura et al. 2009) suggest that for the vast majority of objects i is < 20deg).
As was realized by Osterbrock (1978), the statistics of line widths imply that, in addition to Keplerian motion, there has to be a substantial additional component of velocity perpendicular to the orbital plane. Osterbrock appropriately called this "turbulence". The vertical component is also necessary for the reconciling the structure of the BLR with its kinematics. As Mannucci, Salvati, & Stranga (1992) showed, for NGC 5548 the combined constraints of reverberation mapping and time-averaged line profile and favor the sort of "bird's nest" BLR distribution shown in Figs. 6 and 7.
In summary, I believe that all the evidence points to the BLR having a nest-like appearance and having velocity components:
 |
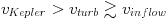(1) |
where the Keplerian velocity, vKepler, of an emission line is a couple of times larger that the turbulent velocity, vturb, which is in turn somewhat bigger than the inflow velocity, inflow. The ratios of BLR height to radius and of vKepler to vturb are similar to those deduced by Osterbrock (1978). The only change to the Osterbrock model is recognizing that there is also a significant inflow.
2 The BLR was first used to estimate masses of AGN black holes by Dibai (1977) who estimated BLR sizes using photoionization considerations. At that stage, of course, there was no clear evidence that the BLR was virialized. See Bochkarev & Gaskell (2009). Back
3 or at the very least to fear that, like the White Queen in Alice in Wonderland, they might have to believe in six impossible things before night lunch! Back
4 The narrow-line region is creating a similar problem. People who study extended narrow-line emission associate it with jets and outflows, while other people are using narrow-line velocity widths as a proxy for the stellar velocity dispersion (see Gaskell 2009a). Back
5 Available at http://www.stokes-program.info/ Back
1305 (narrow
symmetric profile shown in red) and C IV
es = 0.5, and
the dashed green line is the profile produced by the same distribution
with