4. LOPSIDEDNESS IN THE CENTRAL REGION

4.1. Stability of central nuclear disks

It is now well established that all galaxies with bulges or spheroids host a massive central black hole (Gebhardt et al. 2000). The central region, or nuclear disk, in galaxies therefore have a gravitational potential very close to the Keplerian. Some similarities exist with proto-planetary systems (Rauch & Tremaine 1996), or with the formation of new stars through accretion disks (Adams et al. 1989, Alexander et al. 2007). The nearly Keplerian potential, with the angular velocity ~ r^-3/2 favors eccentric orbits and m = 1 modes, instead of ~ r^-1 of galactic disks which favor m = 2 perturbations.

Nearly keplerian disks have the particular property that the orbit precession rate is almost zero ( ~ ). If the apsides are aligned at a given time, they will stay so in a _p ~ 0 mode. The self-gravity of the disk makes > , and the orbits differentially precess at a rate ( - ) < 0. However, if the disk self-gravity is not large, a small density perturbation could be sufficient to counteract the small differential precession. Goldreich & Tremaine (1979) showed that in the case of Uranian rings, the self-gravity could provide the slight impulse to equalize the precession rates, and align the apsides. Two kinds of waves could propagate in such disks - slow stable modes, and unstable rapid waves, growing on a dynamical time-scale.

The density wave theory (e. g., Lin & Shu 1964) predicts that in a self-gravitating stellar disk, global spiral modes can develop only between the radial range delimited by the Lindblad resonances, i.e. for m² ( - _p)² < ². Only in gaseous disks, where the pressure forces dominate, acoustic waves can propagate outside this range. Considering the m = 1 waves, for a pure keplerian potential (neglecting the self-gravity of the disk), = , and the perturbations are neutral. If there is some self-gravity in the disk, then ( - ) < 0, there is only an outer Lindblad resonance and a corotation, but no inner resonance (for prograde modes with _p > 0), and therefore the radial range for the development of m = 1 perturbations is quite large.

The study of WKB modes in a non self-gravitating gaseous disk, with truncation radii at the inner and outer boundary, was first done by Kato (1983), who found a region of trapped one-arm waves, with quite low pattern frequency, much lower than the orbital frequency. Adams et al (1989) considered the influence of self-gravity, in order to apply to young stellar objects, which can have accretion disks with masses of the same order as the central stellar mass. The self-gravity of such a disk is sufficient to modify the precession rate of nearly keplerian orbits ( - ) to a common and coherent value. They found a pattern speed which is of the same order as the angular velocity in the disk, and the unstable waves develop with a growth time comparable to the dynamical time-scale. The special shape of modes is shown in Fig. 20.

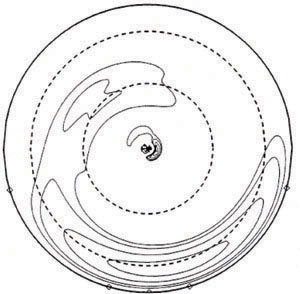Figure 20. Isodensity contours for the lowest order m=1 mode, in a disk of mass equal to the central point mass. Note the shape in alternating "bananas" instead of a continuous one-arm spiral. The dashed lines show the locations of the corotation and the outer Lindblad resonance. From Adams et al. (1989).

Crucial to the development of the perturbations, a special characteristic of the m = 1 mode is to shift the gravity center of the system from the dominant central mass (the black hole for instance), also see Section 3.2.3. In the reference frame of the black hole, this implies the introduction of an inertial force, which by reference to celestial mechanics, is called the indirect term. This term is the mediator of angular momentum exchange between the disk inside and outside corotation and the central mass. The coupling with the outer Lindblad resonance provides the amplification that is usually provided by the corotation in m = 2 modes. A feedback cycle has been proposed by Shu et al (1990), and called SLING (Stimulation by the Long-range Interaction of Newtonian Gravity). The modes depend strongly on the outer disk boundary conditions, since a reflection of short waves is assumed there, in the 4-waves feedback cycle. This cycle is only possible with a gaseous component, since the short waves are not absorbed at the resonance but cross the OLR (Outer Lindblad Resonance).

4.1.1. Slow stable modes, damping slowly

Another possibility to explain central lopsidedness is to exploit the slow modes, that are stable, but can be long-lived, excited by some external mechanism, such as the accretion of a globular cluster or a giant molecular cloud. The precession rate of eccentric orbits is - =0 in the potential of a point mass M_BH, and slightly negative in the presence of a small disk of mass M_d, lighter than the central point mass, with amplitude varying as (M_d / (M_BH)^1/2) or (M_d / M_BH) . If self-gravity has a large enough role, and in particular, if the disk is cold enough and its Jeans length smaller than the disk radius, m = 1 density waves can propagate; their dispersion relation has been studied in the tight-winding limit or WKB approximation (Lee & Goodman 1999, Tremaine 2001). In the linear approximation, the pattern speed for the wavelength = 2 ; / k is in first approximation for (M_d / M_BH) << 1, as given by:

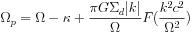(10)

where _d is the surface density of the disk, and F the usual reduction factor that takes into account the velocity dispersion c of the stellar disk, and its corresponding velocity distribution (e.g., Tremaine 2001). The pattern speed then remains of the order of (M_d / M_BH) , for a sufficiently cold disk, and is much smaller than the orbital frequency. These slow waves exist whenever the thin-disk Jeans length _J = c² / G _d is lower than 4 r, while the Toomre parameter Q is less relevant (Lee & Goodman 1999).

The study by Tremaine (2001) shows that disks orbiting a central mass support slow m = 1 modes, which are all stable. Their frequencies are proportional to the strength of collective effects, which is either self-gravity, or velocity dispersion (or pressure in fluid disks). The latter phenomenon can be simulated with softened gravity. There are then two kinds of slow modes: the g-modes (where self-gravity is dominating, and softening is unimportant), which are long waves, with kr << 1, with negative frequency < 0; and the p-modes, which depend on the softening b, which can have both short and long waves (kr ~ b), and with positive frequency > 0; as the softening increases, the amplitude of the mode decreases, as well as .

In numerical N-body simulations of nuclear stellar disks, Jacobs & Sellwood (2001) have reported the presence of a slowly decaying prograde m = 1 mode in annular disks around a slightly softened point mass, but only for disk masses less than 10% of the central mass concentration. This confirms the existence of a persistent slow mode, with positive increasing with the mass of the disk, and decreasing with the amplitude of the perturbation.

Touma (2002) has computed the normal modes of a series of N rings in a thin disk, through linearized dynamics, and using the Laplace-Lagrange secular theory of planetary motions (valid for small eccentricities). The gravity is softened to mimic a hot stellar disk, and varies as the velocity dispersion. The modes are stable when all rings are prograde, but a fraction of only 5% of counter-rotating rings is sufficient to make unstable modes appear. Sambhus & Sridhar (2002) built a model of the M31 nucleus with counter-rotating orbits in a razor thin nucleus, and checked that this amount of counter-rotation could be compatible with observations. The counter-rotating stars could come from a past accreted system, like a globular cluster.

Bacon et al (2001) explored by N-body simulations the possibility of stable m = 1 mode to explain the M31 eccentric nuclear disk. They found that for a disk mass accounting for ~ 20 - 40% of the total central mass, self-gravity is sufficient to counteract the differential precession of the disk. An external perturbation can excite this mode, and it is then long-lasting, over 100 Myr, or 3000 rotation periods. The prograde mode found in the simulations compares well with the p-modes of Tremaine (2001). There is a remarkable agreement between the observed (~ 3 km s^-1 pc^-1 ) and predicted value of the pattern speed, in spite of all approximations, and although the WKB approximation is not satisfied.

Although the slow modes are long-lived, their exciting mechanisms should be found, to explain the high frequency of the phenomenon. The dynamical friction of the m = 1 wave on the stellar bulge has been proposed by Tremaine (1995) as an amplification mechanism, if its pattern speed is sufficiently positive. This amplification results from the fact that the friction decreases the energy less than the angular momentum. The orbits with less and less angular momentum are more and more eccentric, and the m = 1 mode develops. Although the efficiency of the mechanism has not been proven, it should not apply for the slow modes considered here, in a slightly rotating bulge. An external perturbation is more likely to trigger the m = 1 perturbation. There is the possibility of infalling of globular clusters, through dynamical friction, a mechanism explored in the next section. Also interstellar gas clouds should be continuously infalling onto the center, since within 10-100 pc of M31 nucleus, dust lanes, and CO molecular clouds are observed (Melchior et al. 2000). The interval between two such external perturbations (either passage of a globular cluster, or a molecular cloud) in M31 is of the same order of magnitude, so that the external perturbations are an attractive mechanism.

Each episode of m = 1 waves will heat the disk somewhat, but the instability is not very sensitive to the initial radial velocity dispersion. Over several 10⁸ yr periods, the nuclear disk could be replenished by fresh gas from the large-scale M31 disk and subsequent star formation. The hypothesis of cold gas accretion from the disk of M31 itself, has then not only the advantage to trigger the m = 1 perturbation, but also to explain the maintenance of a rather thin and cold nuclear disk.

4.2. Double nuclei by infalling bodies

One solution to the double nuclei problem is to assume that dense stellar systems, like globular clusters, or a dwarf satellite, or even black holes, are regularly infalling into the galaxy center, and are responsible for the observed morphology. Although the events may be relatively rare, their actual frequency is not well-known, and the question remains open as to a possible fit to the observations.

The typical dynamical friction time-scale, for an object of mass M at about 10pc from the center, in a spiral galaxy with a bulge of ~ 10¹⁰ M, typical of an Sb galaxy like M31, is ~ 10⁷ (10⁶ M / M) yr, and it could be much smaller inside. Although short with respect to galactic time-scales, this is much larger than the orbital time of 3 × 10⁵ yr at this radius. Tremaine et al (1975) precisely proposed that the central stellar nuclei in spiral galaxies are the results of many globular clusters infalling by dynamical friction. Typically nuclear stellar systems of 10⁷-10⁸ M would require the infall of a hundred globular clusters. In this frame, the frequency of the event is relatively large, and could be compatible with the observations.

N-body simulations of globular clusters or dwarf galaxies infalling through the gravitational field of a disk, a bulge, and/or a central black hole, have been carried out by many authors (e.g. Charlton & Laguna 1995, Johnston et al 1999, Combes et al 1999, Bekki 2000b), and applied to explain the M31 nucleus morphology (Emsellem & Combes 1997, Quillen & Hubbard 2003). N-body simulations demonstrate that the infalling system is destroyed by the tidal forces of the black hole at the right distance of the nucleus (about 3pc). The debris then rotate around the nucleus in eccentric orbits, and form an eccentric disk. Several hypotheses can then be explored: either the infalling system is alone able to form the nuclear disk (Bekki 2000a), but then its mass corresponds more to the core of a dwarf galaxy having merged recently with the big primary (a quite rare event). Or the infall of the system excites an eccentric mode in the nuclear disk (Bacon et al 2001), as proposed by Tremaine (1995). Also, the presence of the infalling system not yet diluted in the nuclear disk increase the asymmetry. The details of the dynamics, and in particular the inclination of the nuclear disk with respect to the main disk of M31, or the shift of the velocity dispersion peak from the black hole position, due to the systematic rotation of the luminosity peak of the disk, are all explained by the model by Emsellem & Combes (1997), see Fig. 21.

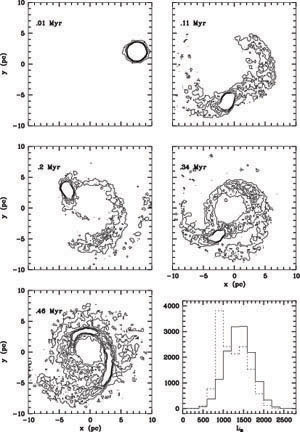Figure 21. Simulation of a globular cluster infall towards a galaxy nucleus containing a massive black hole, fit to the M31 characteristics. The panels show the face-on view contours from the cluster stars, from the start to 0.46 Myr. The bottom right panel shows the histogram of the angular momentum for the cluster particles at the beginning (solid line) and at the end (dashed line) of the simulation. From Emsellem & Combes (1997).

The nature of the infalling system is constrained by the present metallicity and colors of the nuclear disk, especially if the assumption is made that the infalling system is the first one and forms totally the nuclear disk (Bekki 2000a). The observed colors of the double luminosity peaks in M31 are quite similar to the nuclear disk ones, and different from the bulge, so the hypothesis that the nuclear disk is formed from the infalling systems themselves is possible. The hypothesis of globular clusters is more likely, in the sense that the probability to observe it is larger, the friction time-scale being longer, and it requires at least 25 globular clusters to form the nuclear disk. The hypothesis of a dwarf galaxy merger does not correspond to the quite un-perturbed state of the M31 disk. There is some evidence of a past merger around M31, in the shape of an extended stellar disk, loops and shells (Ibata et al 2001, Irwin et al 2005). However, the time to form these stellar streams is much longer than the time-scale for the galaxy core to infall to the center.

It is interesting to discuss in this context the case of the double nucleus in NGC 4486B, which is thought to be similar to the M31 case, but with larger masses, and larger separation (Lauer et al 1996). NGC 4486B is a compact elliptical galaxy, in the outer envelope of M87 in the Virgo cluster. The double nuclei are separated by 12pc, and produce two almost equal luminosity peaks at similar distance from the photo-center, so creating almost no lopsidedness in projection. If explained by a nuclear disk, it is of very small eccentricity. The hypothesis of a past merger as the origin of the two stellar nuclei is weaker in this case, since the environment of the cluster center does not favor mergers.

The idea of infalling systems can be generalized to all galaxy mergers as the origin of lopsidedness. In particular, mergers of galaxies could naturally form eccentric disks. The disk would come from the disruption by tidal forces of one of the stellar core. The presence of massive black holes in each spiral galaxy with bulge, strongly supports this scenario. The end steps of the merger process would form a binary black hole. The destruction of nuclear stellar systems by the tidal forces of the black holes led Merritt & Cruz (2001) to suggest that the existence of low-density cores (and not cusps) in giant galaxies is the consequence of mergers. Further simulations of mergers with central black holes should be performed to explore the formation of eccentric disks.

Somewhat larger-scale asymmetry on scales ~ 1 kpc is also seen in mergers of galaxies and is deduced to be long-lived, as discussed in Section 5.3.

4.3. Core wandering

Some of the nuclear lopsidedness might also be explained through a special oscillation of the central black hole, called "core wandering". This name came from the physics of globular cluster, that was observed to reveal slow oscillation, with a time-scale larger than the crossing time in numerical simulations (Makino & Sugimoto 1987). Miller & Smith (1992) showed by a large series of numerical simulations that a massive nucleus cannot coincide with the mass centroid of its galaxy in a stable way. The type of instability, where the motion of the nucleus implies potential distortions in the center, which trap more particles, is overstable, and reaches a saturation limit. The phenomenon is local, and the time-scale of the oscillation of the nucleus is of the same order as the central dynamical period (cf Figure 22). This core wandering appears physical, and not the consequence of a N^-1/2 random noise oscillation, as tested by simulations with highly varying particle number. In that case, the perturbation amplitude that starts the growth is indeed depending on N, but not the limiting amplitude, nor the growth rate, which is always a few dynamical times. The N^-1/2 phenomenon can be hard to distinguish in small-N simulations, and in globular clusters (Sweatman 1993), but this is not the case for galaxies.

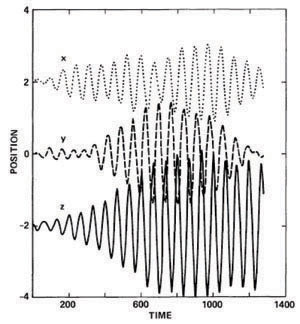Figure 22. Evolution with time of the three coordinates of the "nucleus" consisting in the central 1024 particles, selected from an N-body simulation of 100 352 particles. The saturation of the amplitude of oscillations is visible. From Miller & Smith (1992).

The stochastic part of the core wandering phenomenon has been modeled by Chatterjee et al (2002), separating the force on the central mass in the collective action of the stellar system in which it is embedded, and the fluctuating stochastic force provided by individual stellar encounters. This second force produces a Brownian motion of the central point mass. These motions occur on a time scale much shorter than the time-scale of evolution of the stellar system.

As for the coherent modes of the stellar system coupled to the central mass, the growing oscillation looks like a density wave, and the saturation amplitude of the motion reaches a galaxy core radius. This unstable phenomenon involves the nucleus, even if there is no central black hole in the center, and is also observed in dynamical friction experiments, when the decay of a satellite is studied (e.g. Bontekoe & van Albada 1987). The limiting amplitude of the nucleus oscillation is then reached from above. This kind of oscillation is also observed in spherical galaxies, and continues to develop for a Hubble time (Miller & Smith 1994).

Taga & Iye (1998a) studied the oscillations of a central massive black hole in a rotating galaxy, and also confirmed that the phenomenon is not an N^-1/2 random noise effect, but a true physical phenomenon. They found by N-body simulations that a massive central body can undertake long-lasting oscillations, but only when its mass is lower than 10% of the disk mass. This produces disk oscillations around it. Crucial must be the rotation of the pattern around the center, since it does not vary its amplitude, when the number of particles change. The disk oscillations occur only when the black hole is allowed to move, when the black hole is artificially nailed down to the center, the disk oscillations vanish. They also conclude that the mechanism at the origin of this instability is a density wave, with a fixed pattern as a function of radius.

When the disk around the central mass is fluid, an instability akin to the one proposed by Shu et al (1990) is possible, with a feedback provided by reflection on a sharp edge in the outer disk. Heemskerk et al (1992) estimate that the edge effect is artificial, and studied instead an m = 1 instability arriving only when the masses of the central object and the disk are comparable. There can be angular momentum exchange between the mass and the disk. To simplify their model, they considered only a gaseous disk with a central gap. This instability is confirmed by Woodward et al (1994), and requires the coupling with the central mass, which is displaced from the center, and moves along a smooth, tightly wound, spiral trajectory. Taga & Iye (1998b) found that the sharp edge condition is not necessary, and that an eccentric instability develops in a stellar disk, provided that the central mass is smaller than the disk mass (about 10%), and it is mobile. The eccentric instability then develops a one-arm spiral, with an amplitude that is stronger than when the central mass is fixed to the center. The mechanism is strongly dependent on the softening used, and should be local to the central parts.

4.4. Other mechanisms

If a normal disk around a black hole is not spontaneously unstable to m = 1 perturbations, the modifications of the stellar distribution function F, and in particular the depletion in low-angular momentum orbits, leading to the empty loss-cone phenomenon, can provide the source of instability. If the derivative of F with respect to J is positive, then spherical near-Keplerian systems are neutrally stable (allowing the displacement of the nucleus with respect to central mass), and the flattened non-rotating systems are unstable to m = 1 modes (Tremaine 2005).

Peiris & Tremaine (2003) construct eccentric disk models to represent the double nucleus in M31, and claim that the inner nuclear disk must be inclined by at least 20 degrees with respect to the main disk of the galaxy to represent the data. Although their model is only dynamical, and does not include all the physics, with self-gravity, etc., this suggests that the lopsidedness might be related to a warp or a misalignment. The latter could be the source of dynamical friction against the bulge, and relatively rapid alignment should ensue. A possibility is that the bulge is itself misaligned with the main galaxy disk, which could be due to a recent galaxy interaction (e.g. Ibata et al 2001, Block et al 2006).

Salow & Statler (2001, 2004) compute a more sophisticated model, including self-gravity. They populate quasi-periodic orbits for stars, in the rotating frame with a constant precession speed. The eccentricity of the orbits change sign with radius, so that the apocenter of the orbits change phase in the plane of the nuclear disk (cf fig 23). The resulting best fit model is similar to that obtained with N-body simulations of a strong m = 1 mode in a cold thin disk with a central black hole (Bacon et al 2001). In particular the pericenters of the orbits in the inner and outer disks are in phase opposition. The precession rate, however, is rapid ( = 36.5 km s^-1 pc^-1).

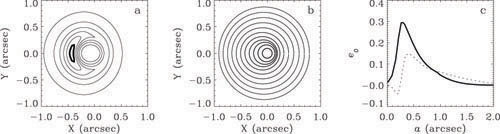Figure 23. (a) Density contours of the best-fit model of the M31 eccentric disk, the central black hole being at (X,Y) = (0,0); (b) uniformly precessing orbits in the total potential. (c) the radial variation of the eccentricity e of orbits, as a function of semi-major axis a: dotted line - the orbit model, with eccentricities changing sign with radius; full line - as a consequence of disk self-gravity, the eccentricity does not change sign any longer. From Salow & Statler (2004).