The origin and the evolution of lopsidedness are not yet well-understood and in fact not received much theoretical attention. The lopsidedness is observed in a variety of tracers and settings. It is observed in old and young stars, and in HI and H2 gas, within the optical disk and far outside the optical disk as seen in the tracer HI gas, and in field galaxies and in galaxies in groups. Given all these parameters it is difficult to come up with a unique physical mechanism for the generation or the maintenance of disk lopsidedness. Indeed there could be multiple paths for it, such as tidal interactions, gas accretion, or an internal instability. The particular mechanism that dominates depends on the situation concerned as can be seen from the following discussion. Towards the end of this section (section 3.4), we give a summary of the most likely physical mechanisms for the origin of disk lopsidedness in spiral galaxies.
We also stress that the standard m = 2 case has been extensively studied for years both analytically as well as by N-body simulations, both in the context of central bars (e.g. Binney & Tremaine 1987, Combes 2008, Shlosman 2005) or as two-armed spiral features (Rohlfs 1977, Toomre 1981). Thus the basic physics of their growth and dynamics is fairly well-understood. In contrast, the m = 1 feature has just begun to be studied. We discuss the physical differences between these two cases (m = 1 and 2), and later in Section 6 a comparison between their observed values is made.
3.1. Kinematical model for the origin of lopsidedness
The simplest way to explain the observed lopsided disk distribution
is to start with a set of aligned orbits and see how long these will
take to get wound up, as was done by
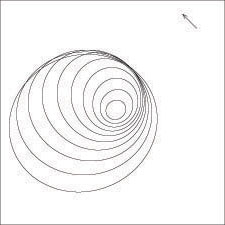
Baldwin et al. (1980),
see Fig. 12. It is
well-known that the differential rotation in a galactic disk would
tend to smear any material feature over a few dynamical timescales.
Baldwin et al. (1980)
showed that on taking account of the epicyclic
motion of the stars, the effective radial range over which the
differential motion affects the winding up is reduced by nearly a
factor of 2, and this helps in increasing the lifetime of the
feature. The net winding up time twinding, for a feature
between two radii R1 and R2
is then given by twinding =
2 
; /
(
-
),
where and
are the angular speed
of rotation and the epicyclic frequency respectively, and
denotes the difference
taken at these two radii. For a flat rotation curve with
= 1.414
, this
gives twinding = 5
[2 ; /
] , which is about
5 times longer than the usual winding up time for material arms.
 |
 |
Figure 12. Left: Pattern
of lopsided
elliptical orbits whose major axes were aligned to begin, following
Baldwin et al. (1980).
The orbits tend to get misaligned with time due to the differential
rotation in the disk. Right: Frequencies
|
|
For the outer parts of a galaxy say at ~ 15 kpc , this is ~ 2 Gyr, which is a few times larger than the local dynamical timescale but is still less that the lifetime of the Galaxy. Hence they argued that the lopsidedness cannot be primordial, and must be generated repeatedly in the disk. Further, this model cannot explain why many isolated galaxies such as M101 show lopsidedness, which is the puzzle they had started out to solve.
Further work on the kinematical origin of lopsidedness due to a cooperation of orbital streams of stars near resonance was done by Earn & Lynden-Bell (1996), with similar results for its lifetime as discussed above. Apart from the short winding time, a generic problem with the kinematical model is that it is not clear what gives rise to the aligned orbits in the first place.
3.2. Dynamical models for the origin of lopsidedness
The set of dynamical models discussed next deal with a more physical origin for the lopsidedness. The most commonly proposed models include tidal encounters, gas accretion, instability in a counter-rotating disk, an off-centered disk in the halo, and ram pressure stripping in a cluster. Of these the most promising are the first two, with the tidal encounters being the dominant mechanism for group galaxies. In addition to these externally triggered processes, the disk lopsidedness could also arise as a global m = 1 instability in self-gravitating disks.
3.2.1. Tidal encounters, and disk response to distorted halo
One of the earliest ideas suggested for generating lopsidedness in a
galaxy was due to a tidal encounter as applied to M101
(Beale & Davies 1969),
although no details were
worked out. It is easy to see that a perturbation as say due to a
tidal encounter between two galaxies with an arbitrary orientation
can generate a force term of
type cos 
,
which can then generate lopsidedness in the galaxy
(Combes et al. 2004,
see Chapter 7.1.1). The other modes will also be
generated but generally m = 1 and 2 are observed to be the strongest
(Rix & Zaritsky 1995).
Also see Section 6 for a discussion the
observed relative strengths of the m = 1 and 2 modes.
In addition to the above direct triggering of lopsidedness as a disk response to the tidal force, it can also be generated more indirectly due to the response of the disk to the distorted halo which feels a stronger effect of the interaction (Weinberg 1995, Jog 1997, Schoenmakers et al. 1997). The details of lopsidedness thus induced will be summarised in this section. The effect can be seen as in the spatial or surface density distribution as well as in the kinematics.
A generally stronger perturbation resulting from the infall of a satellite galaxy can also result in the disk lopsidedness as shown in the N-body simulation study by Walker et al. (1996). Zaritsky & Rix (1997) further used this idea to constrain the rate of infall of satellites onto a galaxy from the fraction of galaxies showing lopsidedness and the star formation, both triggered by the satellite infall. Note that this gives an upper limit on the satellite infall rate if there are other mechanisms which also give rise to the disk lopsidedness; such as gas accretion as discussed in Section 3.2.2.
Since the dark matter halo is more extended than the disk, during a tidal encounter the halo is expected to experience a stronger tidal perturbation on general grounds. Weinberg (1995, 1998) has studied this case numerically for the specific case of the interaction between the LMC and the Galaxy. The live halo shows a strong lopsided response at the resonance points as set by the orbit of the LMC with respect to the Galaxy. The disk response to this distorted halo is shown to be much stronger than the direct lopsidedness triggered in it due to the encounter. A detailed numerical evolution of a galactic disk and the halo perturbed by an impulsive perturbation (Kornreich et al. 1998) shows that m = 1 can grow as a free sloshing libration but can only last for a dynamical timescale. On the other hand, a number of encounters covering a large parameter space for the galaxy mass ratios, orbits, disk inclination were studied by numerical simulations by Bournaud et al. (2005b). They conclude that the resulting lopsidedness can have an amplitude as high as the typical observed value ~ 10% , and it lasts for more than ten dynamical timescales ~ 2 Gyr, after which the lopsidedness drops rapidly.
3.2.1.a Orbits and isophotes in a perturbed disk
We next briefly summarise the results for the orbits, isophotes and kinematics for a disk that is perturbed by a linear lopsided perturbation potential, as say due to a distorted halo (Rix & Zaritsky (1995), Jog (1997, 2000), Schoenmakers et al (1997)) where the halo distortion could be ascribed to a tidal encounter. These equations of motion are general and are applicable irrespective of the mechanism giving rise to the external potential to which the disk responds. This simple model allows one to draw general conclusions about the strength of the perturbation potential by a comparison of results with observations as is shown next.
The details of this approach
(Jog 2000)
are summarised below. The
dynamics of particles on closed orbits in an axisymmetric disk
perturbed by a lopsided halo potential is treated. The cylindrical
coordinate system (R,
) in the
galactic disk plane is used.
The unperturbed, axisymmetric potential in the disk plane,
0(R), and
the perturbation potential,
lop (R) are
defined respectively as:
 |
(1) |
 |
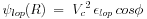(2) |
where 0
(R) represents the typical region of flat
rotation, with Vc being the constant rotational
velocity, as seen in a typical spiral galaxy. This is perturbed by a
small, constant, non-rotating, perturbation potential with a lopsided
form as given by
lop (R). Here
lop is a
small perturbation parameter, which is taken to be constant with radius for
simplicity. That is, a halo with a constant lopsided distortion is assumed.
This is a simple model but it still allows one to understand the
resulting orbits, isophotes and the kinematics in a lopsided galaxy.
Consider a circular orbit at R0. The coupled equations
of motion for the perturbed quantities
R and
are solved
together using the first-order epicyclic theory. The resulting
solutions for the perturbed motion are:
 |
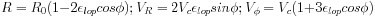(3) |
Thus, an orbit is elongated along
=
180°, that is
along the minimum of the lopsided potential, and it is shortened
along the opposite direction. This result was also noted by
Earn & Lynden-Bell
(1996).
The loop orbits discussed here are not valid for radii much smaller than the disk scalelength (Rix & Zaritsky 1995), but this does not affect the applicability of this analysis to galactic disks because the disk lopsidedness is typically observed only at radii beyond 1.5 disk scalelengths.
The other signatures of the effect of the lopsided perturbation potential are its effect on the isophotes and the kinematics in the disk, discussed next. Since the imaging observations give information on the isophotes rather than orbits, it is necessary to also obtain the isophotal shapes in an exponential galactic disk in a lopsided potential. For an exponential disk, the above approach gives:
 |
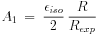(4) |
where iso
is the ellipticity of the isophote
at R, and Rexp is the exponential disk scale
length. Note that here the radii measuring the minimum and maximum
extents of an isophote are along the same axis - unlike in the standard
definition of ellipticity where these two are along directions that
are normal to each other. The resulting isophotes have an
egg-shaped oval appearance, as observed say in M101. Thus, the
azimuthal asymmetry in the surface density or the fractional Fourier
amplitude for m = 1, as denoted by A1
manifests itself as an elongation of an isophote, and both represent
the same underlying phenomenon.
The effective surface density in a self-gravitating, exponential galactic disk may be written as:
 |
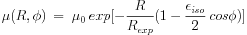(5) |
For a particular isophote, the term in the square bracket is a constant
and hence this formally defines the parametric form of an isophote. Thus
the minimum radius of an isophote occurs along
= 180°
while the maximum occurs along
=
0°; while the opposite is true for
an individual orbit. Thus the isophotes are elongated in a direction
opposite to an orbit, and the elongation
is along the same direction where the maximum effective surface density
occurs - this will be true for any self-gravitating system
(Jog 1997).
To obtain the lopsided potential in terms of the observed lopsided Fourier amplitude, the equations of perturbed motion (eq. [3]) have to be solved with the equation of continuity, and the effective surface density (eq. [5]). Now, the equation of continuity is given by:
 |
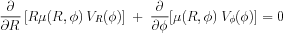(6) |
Solving these, and combining with eq.[4], yields the
following important results (valid for R
Rexp):
 |
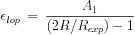(7) |
and,
 |
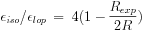(8) |
Thus, the ellipticity of isophotal contours
iso is
higher by at least a factor of 4 compared to
lop. Thus
even a ~ few % asymmetry in the halo potential leads to a large ~ 10%
spatial lopsidedness in the disk. This makes the detection of
lopsidedness easier, and it explains why a large fraction of spiral
galaxies is observed to be lopsided.
For the typical observed values of A1
0.1 at R/
Rexp = 1.5-2.5 (see
Section 2.2), the typical
lop
~ 0.03 (from eqs. [3], and [4]), or ~ 0.05 in view of the
negative disk response discussed next. Thus, from the observed disk
lopsidedness, we obtain a value of the halo lopsidedness. In
the limiting case of high observed A1 ~ 0.3 - 0.4,
the resulting
lop is
still small 
0.1 , this is due
to the high ratio of
iso
/ lop
(eq. [8]). This is an interesting physical result, because it means that
despite the visual asymmetry, such galaxies are dynamically robust.
The above results for orbits and isophotes are shown to be applicable for both stars and gas in the same region of the galaxy since they respond to the same lopsided potential and have comparable exponential disk scale lengths (Jog 1997). This was confirmed by a detailed comparison of the Fourier analysis of the two-dimensional HI data and the 2MASS near-IR representing stars for a few galaxies in the Eridanus group (Angiras et al. 2006) and in Ursa Major (Angiras et al. 2007). The two tracers show comparable lopsided amplitudes (see Fig. 25). This is true even though the HI gas in these group galaxies obeys a gaussian rather than an exponential radial distribution.
In the above analysis, the phase is taken to be constant with radius and hence set equal to zero. When the phase of the potential varies with radius, the resulting isophotes show a prominent one-arm, as observed in M51 and NGC 2997.
3.2.1.b Kinematics in a perturbed disk
The kinematics in the disk perturbed by a lopsided potential is also
strongly affected. The net rotational velocity,
V, (see eq. [3]), is a maximum at
= 0° ,
and it is a minimum along the opposite direction. This results in
distinctly non-axisymmetric rotation curves in the two halves of
a galaxy
(Jog 1997),
with the maximum difference between the rotational velocities ~ 10% or
20-30 km s-1 for the typical observed A1
values
(Jog 2002).
This naturally explains the observed asymmetry in rotation
curves of galaxies such as M101. The observers most often give an
azimuthally averaged data, thereby the precious information on the
kinematical asymmetry is lost. It is strongly recommended (see
Jog 2002)
that the observational papers give, when possible, a
full azimuthal plot of the rotation velocity
or at the very least the average taken in each hemisphere
separately. The latter is done in many papers - see e.g.
Begeman 1987,
which can be used to deduce the kinematical asymmetry in galaxies.
Such asymmetry has also been studied by
Swaters et al. (1999)
from their kinematical data in HI
on DDO 9 and NGC 4395. They show that the rotation curve rises more
steeply in one half of the galaxy than in the other.
The asymmetry in the velocity fields resulting from the disk response to a lopsided halo perturbation has also been studied by Schoenmakers (1999). The results obtained are applied to analyze the kinematical data from a few spiral galaxies (Schoenmakers et al. 1997, Swaters et al. 1999). Schoenmakers et al (1997) show that the Fourier amplitudes m + 1 and m - 1 of the velocity field are affected when the perturbation potential of type m is considered. By comparing the observed values for m = 2 with the calculated values they obtain an upper limit (uncertain up to the sine of the inclination angle) for the lopsided perturbation potential.
The approach described in this section assumes a simplified perturbation lopsided potential with a constant amplitude, also only closed orbits are considered for simplicity. The orbits would change slightly and would not be closed if the random motion of the particles is taken into account. However, this does not affect the isophotal shapes - see Rix & Zaritsky (1995).
3.2.1.c Radius for the onset of disk lopsidedness
The lopsided distribution in a disk cannot self-support itself because
the potential corresponding to it opposes the perturbation potential, as
discussed next. The effective disk surface density or the
disk density response is shown to be a maximum along
=
0°, that is along the maximum of the lopsided potential
(Jog 1997),
see eq. (5) above. This has interesting and subtle dynamical consequences
(Jog 1999).
This can be seen from the self-gravitational potential corresponding to the
non-axisymmetric disk response, which is obtained by inversion of Poisson
equation for a thin disk using the Henkel transforms of the
potential-density pairs. This response potential is shown to oppose the
imposed lopsided potential. This may seem counter-intuitive but it
arises due to the self-gravity of the disk. Thus in the inner parts of
the disk, the disk resists any imposed perturbation potential.
A self-consistent calculation shows that the net lopsided distribution in the disk is only important beyond 1.8 disk scale lengths and its magnitude increases with radius. This indicates the increasing dynamical importance of halo over disk at large radii. The negative disk response decreases the imposed lopsided potential by a factor of ~ 0.5 - 0.7 (Jog 2000). The above radial dependence agrees well with the onset of lopsidedness as seen in the near-IR observations of Rix & Zaritsky (1995). On taking account of this effect, a given observed lopsided amplitude corresponds to the deduced perturbation potential to be higher by a factor of ~ 1.3 - 1.4.
The radius of onset of lopsidedness and the reduction in the imposed potential depend on the form of the perturbation potential which was taken to be constant for simplicity in Jog (1999). A more realistic case with a radially varying perturbation potential as in a tidal encounter with amplitude decreasing at low radii, will result in the highest decrease at lowest radii (Pranav & Jog 2008). In this case the actual value of reduction will decide the radius beyond which net disk lopsidedness is seen.
This idea of negative disk response is a general result and is
applicable for any gravitating system which is perturbed by an external
mechanism. Although it is shown here for a
cos
perturbation resulting from a tidal
perturbation, it is applicable for any linear perturbation of the system.
A similar study for the onset of warps (which can be represented by an
m = 1 mode along the vertical direction) has been done
(Saha & Jog 2006).
This shows the onset of warps from a radius of 4-5 disk scalelengths, in
good agreement with observations
(Briggs 1990).
The disk self-gravity
is more important along the z-direction for a thin disk and hence the
disk is able to resist vertical distortion till a larger radius than the
planar distortion.
3.2.1.d Comparison of A1 vs. tidal parameter
Since tidal encounters (e.g. Beale & Davis 1969, Weinberg 1995) and satellite accretion (Zaritsky & Rix 1997) have often been suggested as the mechanism for the origin of the disk lopsidedness, it is instructive to check how the observed amplitude A1 for lopsidedness varies with the tidal parameter Tp as was done by Bournaud et al. (2005b). The tidal parameter Tp was calculated in each case as:
 |
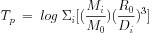(9) |
where the sum is computed over the companions for a galaxy of target mass M0 and radius R0 and Mi is the mass of the companion at a projected distance Di on the sky. The summation is over neighbours within 2 degrees on the sky and within 500 km s-1 velocity range of the test galaxy.
The result is plotted in Figure 13, for the 35 most lopsided galaxies which are at an inclination of < 70°. Surprisingly, this does not show a correlation between the lopsided amplitude and the strength of the tidal parameter. In particular it is hard to explain the galaxies with high A1 and low tidal parameter (in the top l.h.s. of this figure) in the tidal picture. On the other hand, this still does not rule out tidal encounters as the origin for lopsidedness if it is long-lived, or if it arises due to a satellite merger (Walker et al 1996, Bournaud et al. 2005b).
 |
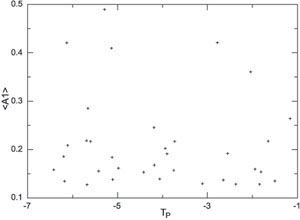Figure 13. Plot of A1 vs. tidal parameter for the 35 strongly lopsided galaxies in the OSU sample (taken from Bournaud et al. 2005b). There is no correlation between these quantities, in particular the isolated galaxies with high A1 (top l.h.s. corner of this plot) cannot be explained by a recent tidal interaction. |
In order to check the typical values of lopsided amplitudes generated in tidal encounters and satellite accretion, N-body simulations for a number of encounters and satellite mergers were studied. They included the tidal encounters between nearly equal-mass galaxies (up to the ratio of 4:1) and mergers of small-mass galaxies (in the ratio of 5:1-20:1) (Bournaud et al. 2005b). It was found that tidal interactions can indeed generate a fairly large amplitude similar to or higher than the average value of ~ 0.1. However, the amplitude then drops rapidly and hence can be seen only for < 2 Gyr. A typical example of an encounter between a 2:1 mass ratio is shown in Figure 14. Thus tidal encounters cannot explain the high amplitude of lopsidedness seen in several isolated galaxies such as NGC 1637, although it could arise due to a recent satellite accretion. While a satellite accretion of mass ratio 7:1-10:1 can result in a strong lopsidedness, it can also thicken the disk more than is observed (Bournaud, Combes, & Jog 2004, Bournaud et al. 2005a). The thickening of disks can set a limit on the rate of satellite mergers (Toth & Ostriker 1992). It needs to be checked if a small-mass satellite falling onto a galactic disk can generate the right amplitude distribution of lopsidedness without thickening the disk, and further if there exist satellites in sufficient numbers to fall in at a steady rate to repeatedly generate lopsidedness as required by the observed high fraction of lopsided galaxies.
 |
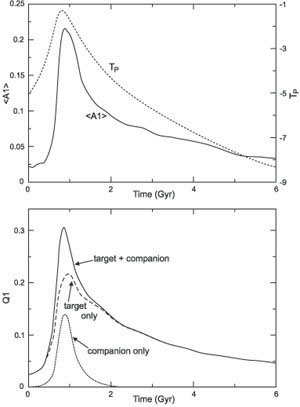Figure 14. Plot of A1 vs. time in the middle radial range of 1.5-2.5 disk scalelengths, generated in a distant interaction between galaxies of mass ratio 2:1 (taken from Bournaud et al. 2005b). The peak value of A1 is large ~ 0.2, higher than the average value seen in the OSU field galaxies sample, but it drops rapidly to 0.05 in a few Gyr. The lower panel shows the same in terms of Q1, the cumulative potential from the disk. |
The mechanism for origin of lopsidedness involving a tidal encounter has been explored by Mapelli et al. (2008) in the context of NGC 891. They show that the lopsidedness seen in the atomic hydrogen gas in NGC 891 is due to the fly-by encounter with its neighbour UGC 1807. They argue that this is a preferred mechanism over gas accretion from cosmological filaments or that due to ram pressure from the intergalactic medium.
Further, a number of statistical features for the field galaxies show that a tidal encounter cannot be the primary mechanism for the origin of the disk lopsidedness- for example, the lopsidedness is higher for late-type galaxies whereas tidal encounters and mergers would tend to lead to the secular evolution of a galaxy towards early-type galaxies. Thus if tidal interactions were the primary mechanism for generating lospidedness, then the early-type galaxies should show a higher amplitude of lopsidedness. This is opposite to what is sen in the field galaxies (Bournaud et al. 2005b). Thus other mechanisms such as gas accretion (Section 3.2.2) could be important in generating the lopsidedness in field galaxies.
In the group galaxies, on the other hand, the tidal interactions being more frequent, play a dominant role in generating lopsidedness. This is evident from the fact that the early-type galaxies show higher lopsided amplitudes as seen in the Eridanus group galaxies (Angiras et al. 2006) and less strongly in the Ursa Major group of galaxies (Angiras et al. 2007). The details are given in Section 5.
3.2.2. Gas Accretion, and other mechanisms
The intergalactic gas accretion was proposed as a qualitative idea to explain the m = 1 asymmetry in NGC 4254 by Phookun et al. (1993). They proposed that the lopsidedness could arise due to the subsequent swing amplification in stars and gas (as in Jog 1992). An extensive study of origin of lopsidedness via N-body simulations (Bournaud et al. 2005b) shows that while tidal encounters can explain the observed amplitudes of disk lopsidedness, these cannot explain the various observed statistical properties such as the correlation between A1 and A2, and the higher lopsidedness seen for the late-type field galaxies. In order to do this, one needs to take account of gas accretion from outside the galaxy.
There is growing evidence that galaxies steadily accrete gas from the external regions, as seen from the cosmological models (Semelin & Combes 2005), and also observed in nearby galaxies (Sancisi et al. 2008). Thus it is natural to see how this affects the mass distribution in a disk. While the details of gas infall are not yet well-understood, it is plausible that a galaxy may undergo an asymmetric gas infall on the two sides from say two different external filaments. An application of this idea showed that the gas infall and the resulting star formation can well reproduce the striking asymmetry observed in NGC 1367 (Bournaud et al. 2005b), see Fig. 15 here.
 |
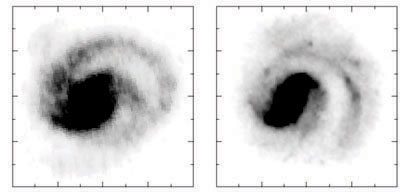Figure 15. NGC data - near-IR data (left panel), and the same from N-body simulations with gas accretion in two streamers at a rate so as to double the mass of the galaxy in a Hubble time (right panel), taken from Bournaud et al. (2005b). |
A word of caution is that if gas accretion is the mechanism for generation of lopsidedness, one would expect to see asymmetry in the gas velocity fields whereas these are smoothly continuous as pointed out by Baldwin et al. (1980). In the case of galaxies in groups, in any case, the tidal interactions may play a dominant role, see Section 5.2 for the details.
Other physical models have also been developed in the literature but these are probably not as widely applicable due to the specific parameters or conditions chosen, as discussed below. This includes a proposed model where the growth of m = 1 is treated as an instability in a self-gravitating disk (Lovelace et al 1999). This results in strongly unstable eccentric motions but only within the central disk scalelength. Here a linear analysis is used to treat slowly growing mode, and the pattern speed could be either positive or negative. In another model where the disk is off-centered with respect to the halo up to a maximum distance of the core radius (Levine & Sparke 1998) also shows lopsidedness. However, it is seen only in the inner regions within the core radius of the halo where the halo density and hence the rotation speed is constant. Both these papers do not yield higher lopsidedness in the outer parts, and this result contradicts the observations which preferentially show lopsidedness in the outer parts of a galaxy. The kinematical and morphological asymmetries resulting from the latter model are shown to be not always correlated (Noordermeer et al. 2001). This is somewhat unexpected - since on general physical grounds the two would be expected to be related causally (see Section 2.2). In any case, the restricted set of initial conditions required for this model makes it applicable only to a few galaxies such as the dwarf galaxies.
A self-consistent model for m = 1 in a self-gravitating disk has been proposed by Syer & Tremaine (1996) in the so-called razor-thin disks. However, the density response due to an imposed perturbation opposes the perturbing force (see Jog 1999) and hence the disk asymmetry cannot result from the orbital asymmetry as was also argued by Kuijken (1993) and Earn & Lynden-Bell (1996). Moreover, the model by Syer & Tremaine (1996) gives the density response to be maximum along the perturbed force, which is in contrast to the result by Rix & Zaritsky (1995), and Jog (1999).
3.2.3. Lopsidedness as an instability
An obvious possible explanation for the origin of the lopsided mode is that it arises due to gravitational instability in the disk. For example, this was proposed and studied for the gas by Junqueira & Combes (1996). A similar model for the disk in a dark matter halo perturbed by a satellite was studied by Chan & Junqueira (2003), however these models generate lopsidedness only in the inner regions in contrast to the observed trends. An internal mechanism based on the non-linear coupling between m = 2 (bars or spiral arms) and m = 3 and m = 1 has been proposed by Masset & Tagger (1997) which gives rise to the excitation of m = 1 modes in the central regions.
Lopsided instabilites have been shown to develop in counter-rotating stellar disks which have a high fraction of retrograde orbits (Hozumi & Fujiwara 1989, Sellwood & Valluri 1997, Comins et al 1997, Dury et al 2008). Galaxies where the gas participates to the counter-rotation are quite often observed to develop m = 1 perturbations (e.g. Garcia-Burillo et al 2000, 2003). However, since counter-rotation is rarely seen in stellar disks (Kuijken, Fisher, & Merrifield 1996, Kannappan & Fabricant 2001, McDermid et al 2006), this cannot be the primary mechanism for the generation of lopsidedness in disks.
In a recent work, the self-gravity of a slowly-rotating global m = 1 mode has been shown to lead to a long-lasting lopsided mode in a purely exponential disk as in a spiral galaxy (Saha, Combes, & Jog 2007). This model was motivated by the fact that the observations show that the lopsidedness has a constant phase with radius which indicates a global mode. Further, it was noted that m = 1 is unique in that the centre of mass of the disturbed galaxy is shifted away from the original centre of mass and thus acts as a restroing force on the latter. Thus the system can self-support the m = 1 mode for a long time especially when one takes account of the self-gravity of the global mode.
Using the linearized fluid equations and the softened self-gravity of the perturbation, a self-consistent quadratic eigenvalue equation is derived for the lopsided perturbation in an exponential galactic disk and solved. Fig. 16 shows the resulting isodensity contours, clearly the centres of isocontours are progressively more disturbed in the outer parts.
 |
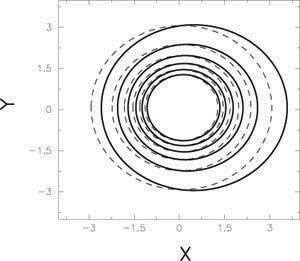Figure 16. Contours of constant surface density for a global m = 1 mode, taken from Saha et al. (2007). Here the x and y axes are given in units of the disk scalelength. The maximum surface density occurs at (0,0). The outer contours show a progressive deviation from the undisturbed circular distribution, indicating a more lopsided distribution in the outer parts - as observed. |
The self-gravity of the mode results in a significant reduction in the differential precession, by a factor of ~ 10 compared to the free precession. This leads to persistent m = 1 modes, as shown in Fig. 17.
 |
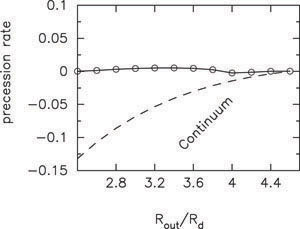Figure 17. The precession rate for the
global lopsided mode vs. the size of the disk in units of the disk
scalelength in a galactic disk (shown as the line with circles)
is very low, thus the mode is long-lived. The dashed line denotes the
free precession ( |
N-body simulations are performed to test the growth of lopsidedness in a pure stellar disk, which confirm these results (see Fig. 18). Both approaches are compared and interpreted in terms of slowly growing instabilities on timescales of ~ a few Gyr, with almost zero pattern speed.
 |
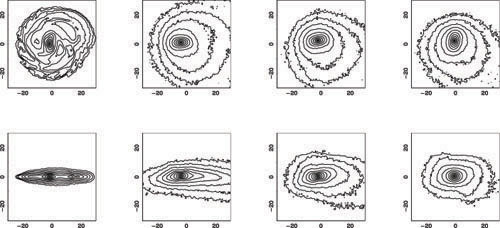Figure 18. The isodensity contours in a purely stellar exponential galactic disk, given in a logarithmic scale of the surface density of the stellar disk, face-on (top panel) and edge-on (lower panel) views at four different epochs: T = 0, 4.8, 9.6, 14.4 Gyr, from left to right, taken from Saha et al. (2007). The global lopsided mode is long-lived and lasts for ~ 14 Gyr. |
Though this is a somewhat idealized approach, it is precisely this that has allowed the authors to focus on the basic dynamics of the excitation and growth of m = 1 modes. For example, here the only important input parameters are the softening and the Toomre Q parameter. A smaller value of Toomre Q results in a fast initial growth of the mode but later as the Q increases due to the heating in the system, the mode is self-regulated and has a nearly constant amplitude A1 that is long-lived. The softening acts as an indicator of the coherence in the mode, and a higher value results in a faster growth rate of the modes. These global modes are precessing remarkably slowly, and therefore are relatively long-lived. Numerical analysis of the eigen modes of a cold thin disk shows that, if treated as modes of zero pattern speed, warps and lopsidedness are fundamentally similar in nature (Saha 2008).
Such small pattern speed is also in agreement with the work of Ideta (2002) who showed that the rotating m = 1 mode in a live halo would be damped very rapidly by the density wake induced in the halo, see Fig. 19. Hence he argued that the m = 1 modes must be non-rotating at a rate smaller than 1 km s-1 kpc-1. This would give the damping time to be comparale to the Hubble time, which can explain the high frequency of lopsidedness seen in spiral galaxies.
 |
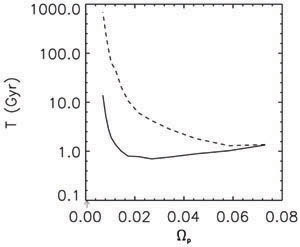Figure 19. The damping time of the lopsided mode vs. the pattern speed, for a self-gravitating case (solid line) and without self-gravity (dashed line) respectively, taken from Ideta (2002). Damping times ~ Hubble time imply a very low pattern speed of the lopsided mode. |
In a recent paper Dury et al. (2008) have studied a galactic disk in an inert halo by N-body simulations and argued that that a rotating m = 1 mode can occur as a result of the swing amplification (Toomre 1981).
3.2.4. Effect of inclusion of rotation and a live halo
The work by Saha et al. (2007) shows that a gravitating disk is susceptible to the growth of m = 1 modes, irrespective of the origin of these modes. These could be triggered as a response to a distorted halo, or by gas accretion. We caution, however, that Saha et al. (2007) treat a simple, specialized case of slow rotating modes in a pure exponential disk. A more realistic treatment should include a live or a responsive halo in addition to the disk. Here more parameters enter the picture such as the relative mass of the halo and the disk, and ratio of the core radius of the halo to the disk scalelength etc. The inclusion of a live halo is expected to further support the persistent m = 1 modes, in analogy with what was shown for bars by Athanassoula (2002) and for a general, local non-axisymmetric feature by Fuchs (2004). In contrast, other papers suggest that a responsive halo tends to damp a feature in the disk by the wake created in the halo. This was shown for disk lopsidednesss (m = 1 in the plane) by Ideta (2002), and shown in the case of warps treated as an m = 1 mode normal to the galactic plane (Nelson & Tremaine 1995). This issue needs to be clarified by further dynamical studies of a global m = 1 mode of an arbitrary pattern speed in a galactic disk. This study should include a live halo, and have a high resolution (since poor resolution may smoothen the response and give a spuriously long-lasting mode), with the aim to check the lifetime of such a mode.
A lopsided mode in a collisionless spherical dark matter halo is shown to be long-lasting or slowly damped compared to the dynamical timescales (Weinberg 1994, Vesperini & Weinberg 2000). However it is not clear if this is due to the fact that the halo is supported by random motion and hence a perturbation in it is long-lived. On the other hand, in a spiral galaxy, the presence of differential rotation puts a limit on any material feature due to the precession rate. In contrast, the numerical simulations of perturbations triggered in a galaxy with live halo, due to the tidal encounter of nearly equal-mass galaxies (up to the ratio of 4:1) and mergers of small-mass galaxies (in the ratio of 5:1-20:1) show that the lopsidedness thus generated, although long-lived compared to the dynamical timescales, does not last beyond ~ 2 Gyr (Bournaud et al. 2005b). The crucial factor that decides the lifetime of the lopsided mode could be its pattern speed, with the small speed cases lasting for a long-time close to the Hubble time (Ideta 2002, Saha et al. 2007). The off-centering of the mass distribution is less pronounced in the case of high rotation speed. This could lead to a short lifetime of the m = 1 mode as pointed out by Ideta (2002). In this case the restoring term in the equations of motion (Saha et al. 2007, eq. 18) is less pronounced and hence the m = 1 mode lasts for a shorter time. Alternatively, it could be that the wake generated in a halo could be larger for a higher pattern speed, and hence the halo tends to dampen such modes. This may be the reason why the lopsidedness generated in a disk with a live halo due to a tidal encounter or a minor merger (Bournaud et al. 2005b) lasts for < 2 Gyr.
While slow m = 1 modes are shown to be long-lived, the uniqueness of this solution is still not established, or that this is what explains the observed lopsidedness. Also it is not clear what would excite such slow modes. The generating mechanism may have a strong bearing on the resulting pattern speed: a tidal encounter is expected to result in lopsidedness with a high pattern speed ~ the relative velocity over the impact parameter as argued by Ideta (2002). Gas accretion, on the other hand, may not easily give a global m = 1 mode, while observations show the mode to be global. Further numerical simulations should check if a satellite accretion can give rise to a slow, global mode. An actual measurement of the pattern speed of the lopsided mode in a real galaxy will help settle this issue, and we urge observers to take up this important measurement.
3.3. Comparison between origin of m = 1 and m = 2; stars and gas
As discussed at the beginning of Section 3, the m = 2 case is fairly well-understood, while the m = 1 case has only begun to get attention from theorists. There are several differences in the dynamics and evolution of the two features, and also as applied to stars or gas. First, the presence of dark matter halo is likely to have a substantial role to play in the origin and evolution of lopsidedness in a disk. This is especially true in the outer parts of a disk since the disk lopsidedness is observed to increase with the radial distance where the halo is more important. In the inner regions of a galaxy, on the other hand, the inclusion of the bulge is likely to play an important role in stabilizing the m = 1 mode (de Oliveira & Combes 2008).
Further, the m = 1 mode generally has no ILR (Inner Lindblad Resonance, e.g., Block et al. 1994) hence its evolution differs from that of m = 2. The m = 1 mode does not get damped easily due to the angular momentum transport occurring at the resonance points as in the case of m = 2 (Lynden-Bell & Kalnajs 1972). In case of m = 2 this causes an absorption of the wave at the ILR and thus a break in the feedback loop. But in absence of an ILR for m = 1, this break does not arise and this helps in sustaining the global m = 1 mode for a long time. In this picture, the gas being cold behaves in a different way. The absorption at the resonance point is only partial for gas and hence even m = 2 can be sustained in gas despite the presence of an ILR. This helps support the generation of m = 2 and higher order modes in the presence of gas.
3.4. A summary of the various mechanisms
Of the various mechanisms proposed so far, the most promising ones, as judged by the resulting agreement with the observations, are those involving tidal encounters and gas accretion.
An m = 1 perturbation in a disk leads to a shift in the centre of mass in the disk, and this then acts as an indirect force on the original centre of the disk. The disk is thus shown to naturally support an m = 1 mode, and as pointed out above, this is a characteristic property valid only of a lopsided mode. This basic physics is sometimes clouded over because of the additional effects introduced due to the inclusion of the dark matter halo, the bulge, and the gas as in a real galaxy. Further, depending on whether the halo is live or rigid, and whether it is pinned or not, and whether the pattern is rotationg or stationary can lead to additional complexities. Also, other features like the wandering of the centre (Miller & Smith 1992) may introduce an m = 1 mode. In short, there seem many paths to get m = 1 in a galaxy, and therefore it is important to identify which is the most applicable one in a real galaxy.
Long-term maintenance of disk lopsidedness
It has been realized from the beginning that the lopsided modes should be fairly long-lived (e.g., Baldwin et al. 1980) or excited frequently. This is needed in order to explain the high fraction of galaxies showing lopsidedness, and also the strong lopsidedness seen in isolated galaxies like M101. It has been noted that since m = 1 does not have an ILR, it should be the preferred mode in the galactic disk (Section 3.3). This, however, does not say anything directly about its lifetime. The persistence of lopsided mode is still an open question, as shown by the discussion below.
While tidal encounters can generate the right lopsided amplitudes, these are not correlated with the strength of a tidal encounter (Bournaud et al. 2005b), or with the presence of nearby neighbors (Wilcots & Prescott 2004). This could be explained if the disk lopsidedness once generated either directly in the disk, or as a response to a long-lived halo distortion, were long-lived, so that there is no clear correlation with a tidal encounter. N-body simulations with a live halo show the resulting m = 1 modes in the disk to last for ~ 2-3 Gyr, which is much smaller than the Hubble time, thus these need to be triggered again. A tidal encounter will typically generate a fast mode which is expected to be not long-lived (see the discussion in Section 3.2.3).
While the satellite accretion of mass ratio 7:1-10:1 can result in a strong lopsidedness, it can also thicken the disk more than is observed (Bournaud et al. 2004). Also, it has a short lifetime of < 2 Gyr (Bournaud et al. 2005b). It further needs to be checked if a smaller-mass satellite falling onto a galactic disk can generate the right amplitude distribution of lopsidedness without thickening the disk, and if there are adequate number of such satellites that can fall in at a steady rate.
The pattern speed is expected to have a significant effect in determining the lifetime of a lopsided mode with a slow patttern being long-lived. It is not clear if a live halo will help or hinder the long-term sustenance of an m = 1 mode, as discussed in Section 3.2.3.
Future work needs to study the long-term maintenance of m = 1 modes when generated by accretion of a low-mass satellite. A similar study needs to be done for the case of gas accretion and to see if the latter gives a global mode. The observations of group galaxies with their generally stronger and frequent triggering of lopsidedness (see Section 5) can act as a constraint on any generating mechanism proposed for the field galaxies.