2. ARE THE RADIO STRUCTURES IN A STATE OF MINIMUM ENERGY?

2.1. Calculation of the minimum-energy field

The magnetic field strength and particle spectrum are important for jet physics as they define the internal pressure. The level of synchrotron radiation depends on the magnetic-field strength and the number of relativistic electrons and positrons, but these quantities are inseparable based on the observed synchrotron radiation alone. To progress further it is usual to assume that the source is radiating such that its combined energy in relativistic particles and magnetic field is a minimum [35]. In this situation the energy in the magnetic field is ~ 3/4 of the energy in the relativistic particles, and so this is similar to the condition in which the two are equal and the source is in `equipartition'. A change in any direction of the ratio of energy density in particles to magnetic field increases the total energy and pressure in the emitting plasma.

The minimum-energy magnetic field for a power-law spectrum of electrons producing radiation of a measured flux density at a particular frequency can be calculated analytically (e.g. 220), and for more complicated spectra the results can be obtained via numerical integration. Physical insight can be gained by considering a power-law spectrum where electrons give rise to a synchrotron luminosity, L, at a given frequency of the form

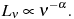(1)

It is now normally thought preferable to define the spectral limits via a minimum and maximum Lorentz factor for the electrons in the source frame, _min and _max, (e.g. 220), rather than as synchrotron frequencies in the observer's frame (e.g. 147), since the former is related to acceleration processes and has the potential for being chosen on a physical basis. Except in the special case of = 0.5, the minimum-energy magnetic field strength, B_me, is given by

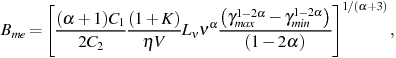(2)

where V is the source volume, and C₁ and C₂ are combinations of fundamental physical constants and functions of given by synchrotron theory (for details see [220]). Following the notation of [147], K is the ratio of energy in other relativistic particles to that in the electron and positron component, and is the fraction of the volume filled by particles and fields (the so-called filling factor). The true minimum energy is when the only relativistic particles are radiating leptons, and the volume is completely and uniformly filled with radiating particles and fields. Some authors consistently use these assumptions when calculating B_me. If K > 0 or < 1 then B_me is increased. Results for B_me are more strongly dependent on _min than _max, since > 0.5 for most observed radio spectra.

Relativistic beaming of a source affects B_me (as considered later in Section 3.2). Since there is inevitably uncertainty in the value of beaming parameters, B_me is best measured in components for which bulk relativistic motion is believed to be small or negligible. Of course, even in the absence of relativistic beaming, the angle to the line of sight, , enters into the calculation via a correction from projected linear size into true source volume, V. Typical values found for B_me in radio lobes and hotspots are 2-200 µGauss (0.2-20 nT) (e.g. 119), although a hotspot field as large as 3000 µGauss has been measured [91].

Figure 3 shows the dependence of B_me on _min, K, , and , separately for electrons giving rise to synchrotron spectra with = 0.6 and = 1.1. The former slope is as expected from electrons undergoing highly relativistic shock acceleration [1], and the latter where energy losses have steepened the spectrum. The curves show that B_me changes rather little (within factors of at most a few) for rather large changes in the input assumptions.

Figure 3. Effect on the calculated minimum-energy magnetic field if a parameter value is varied from its nominal value (left-hand-side of plot). Results are for a power-law electron spectrum, extending from Lorentz factor min to max = 105, that gives rise to a synchrotron spectrum S - with = 0.6 (solid lines) and = 1.1 (dashed lines). (a): increasing min from a value of 10. (b): increasing the ratio of energy in other particles to that in electrons, K, from a value of zero. (c): decreasing the filling factor, , from a value of 1. (d) decreasing the angle to the line of sight, and thus increasing the source volume from the projected size at = 90°.

2.2. Using X-rays to test minimum energy

The minimum-energy assumption can be tested by combining measurements of synchrotron and inverse-Compton emission from the same electron population. If the inverse Compton process is responsible for most of the X-ray radiation that is measured, and the properties of the photon field are known, the X-ray flux density is proportional merely to the normalization of the electron spectrum, , if the usual power-law form

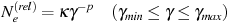(3)

is assumed, where N_e^(rel) is the number of relativistic electrons per unit . The upscattered photons might be the CMB, whose properties are well known. Alternatively they could be the radio synchrotron radiation itself, in the process known as synchrotron self-Compton (SSC), or photons from the active nucleus, particularly at infrared through ultraviolet frequencies. Since the available photons range in frequency, so too do the energies of electrons responsible for scattering them into the X-ray, and these are rarely the same electrons for which the magnetic field is probed through synchrotron radiation. Nevertheless, it is usual to assume that the magnetic field, photons, and relativistic electrons are co-located, with the synchrotron photon density proportional to B¹⁺. Here is defined as in Equation 1, and theory gives = (p - 1) / 2. The combination of synchrotron (radio) flux density and inverse Compton (X-ray) flux density then allows a value for the magnetic field strength, B_SiC, to be inferred and compared with B_me.

Since the modelling requires that the volume and any bulk motion of the emitting plasma be known, the best locations for testing minimum energy are the radio hotspots, which are relatively bright and compact, and are thought to arise from sub-relativistic flows at jet termination (but see [80]), and old radio lobes where the plasma may be relatively relaxed. There is no reason to expect dynamical structures to be at minimum energy.

It was anticipated that Chandra and XMM-Newton would make important advances in tests of minimum energy, since already with ROSAT and ASCA there were convincing detections of inverse Compton X-ray emission from the hotspots and lobes of a handful of sources (e.g. 101, 76, 195), and pioneering work on the hotspots of Cygnus A had found good agreement with minimum energy [101]. Chandra and XMM-Newton have allowed such tests to be made on a significant number of lobes and hotspots, with results generally finding magnetic field strengths within a factor of a few of their minimum energy (equipartition) values for K = 0 and = 1 (e.g. 95, 33, 110, 51, 30, 10, 54, 148). A study of ~ 40 hotspot X-ray detections concludes that the most luminous hotspots tend to be in good agreement with minimum-energy magnetic fields, whereas in less-luminous sources the interpretation is complicated by an additional synchrotron component of X-ray emission [98]. Considerable complexity of structure is seen where hotspots are close enough for X-ray images to have kpc-scale or better resolution (e.g. 126).

For radio lobes, the largest systematic study where it is assumed that all the X-ray emission is inverse Compton radiation is of 33 FRII lobes, and finds 0.3 < B_SiC / B_me < 1.3 [55]. Since the asymmetry is on the side of B_SiC < B_me, it is important to recognize that the analysis may not have accurately taken into account contributions to the lobe X-ray emission from cluster gas, now commonly detected away from the lobe regions in FRII radio galaxies ([12], and see Fig. 2). However, as seen in Figure 4, the lobe X-ray emission from cluster gas would have to be far brighter than that from inverse Compton scattering to cause B_SiC / B_me to increase significantly (e.g., from 0.5 to 1.0), and this is incompatible with the observation that lobes stand out in X-rays as compared with adjacent regions.

Figure 4. The amount by which the fraction of the total X-ray flux density attributable to inverse Compton radiation, X-rayiC / X-raytotal, would have to be reduced for a result of BSiC / Bme = 0.5 to be increased. Solid and dashed curves are for = 0.6 and = 1.1, respectively.

Better agreement between B_SiC and B_me would be achieved if B_me has been overestimated. Figure 3 shows that decreasing the filling factor or including relativistic protons that energetically dominate the electrons have the opposite effect. A decrease in B_me is found if the source has been assumed to be in the plane of the sky whereas it is really at a small angle, with the structures having more volume. However, the small angles required to make an appreciable difference would be inconsistent with random sampling. More promising would be if _min were higher than typically assumed, as stressed by [27] who claim evidence for a value of _min as high as ~ 10⁴ in the hotspot of one FRII radio galaxy, with a lower value of _min ~ 10³ in the lobes as a result of adiabatic expansion. This is in line with earlier measurements of spectral flattening at low radio frequencies in hotspot spectra, suggestive of values of _min no lower than a few hundred (e.g. 133, 41). Why there might be such a _min in a hotspot is discussed by [91].

It is important to stress that finding B_SiC / B_me within a factor of a few of unity does not allow strong constraints to be placed on physical parameters. As shown in Figure 3, large changes in input parameters do not change B_me, and thus B_SiC / B_me, by a large amount. It is often pointed out that if the magnetic-field strength is a factor of a few below B_me, the energy in relativistic electrons must dominate the magnetic-field energy by orders of magnitude. While this is relevant for understanding the state of the plasma, does this really matter from the point of view of source energetics? The increase in combined electron and magnetic-field energy over the minimum energy is relatively modest as long as the electron spectrum is not very steep and the field strength is no less than about a third of B_me (Fig. 5).

Figure 5. The ratio of total energy in electrons and magnetic field, computed from combined X-ray inverse Compton and radio synchrotron measurements, to that calculated for minimum energy, for the range of BSiC / Bme typically observed. Solid and dashed curves are for = 0.6 and = 1.1, respectively.

In any case, it is clear that application of minimum energy over large regions is an oversimplification. Three-dimensional magneto-hydrodynamical simulations that incorporate particle transport and shock acceleration [201, 202] find much substructure of particle distributions and fields within the volumes typically integrated over observationally. Complexity on a coarser scale is seen in some observations (e.g. 110, 148).