3. DO POWERFUL LARGE-SCALE JETS HAVE FAST SPINAL SPEEDS?

3.1. The impetus from PKS 0637-752

Chandra is central to the current debate concerning jet speed in the powerful radio jets of quasars. The work was kick-started unexpectedly. Observing quasars was not initialy a high scientific priority for Chandra, as it was recognized that the cores were bright, and the likelihood of multiple photons arriving between CCD readouts was high, leading to distorted spectral measurements (so called `pileup'). It was thus fortuitous that a radio-loud quasar was the chosen target for in-flight focus calibration, since this led to the detection of resolved jet emission from the z = 0.651 quasar PKS 0637-752 ([177, 45], and see Fig. 6).

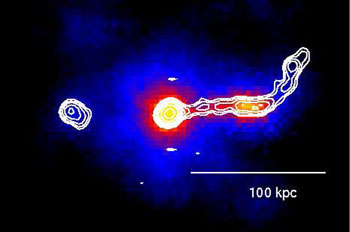Figure 6. The z = 0.651 quasar PKS 0637-752, using data from [177]. The plot shows a smoothed Chandra X-ray image of ~ 35 ks exposure with radio contours from an 8.64 GHz ATCA radio map (beam size 0.96" × 0.81"). X-ray emission is detected from the nucleus and from the western radio jet before it bends north. The bright jet region 7.8" west of the nucleus is known as Knot WK7.8.

Several possible origins for PKS 0637-752's jet X-rays were considered. The level of optical emission was too low to explain the X-rays as the synchrotron radiation from a single population of electrons, and SSC was disfavoured as it would require strong dominance of the energy in relativistic electrons over that in magnetic field, giving a total energy in particles and field that is ~ 1000 times that given by minimum energy [177]. A more promising explanation allowed the jet to be at minimum energy but required it to have fast bulk motion (a Lorentz factor of ~ 20 at ~ 5° to the line of sight), in which case it would see boosted CMB in its rest frame and emit beamed X-rays in the observer's frame [197, 44]. Although such a speed and angle are consistent with VLBI measurements on pc scales [139], the fast speed must persist up to hundreds of kpc from the core (after projection is taken into account) for the X-rays to be produced by this mechanism, which I will call "beamed iC-CMB". This explanation ran counter to the common wisdom of the time, based on radio data, that the bulk relativistic speed of quasar jets on the large scale is ~ 2 (e.g. 31, 208). To overcome the contradiction, it was suggested that quasar jets have a fast-moving central spine responsible for the observed X-rays, and a slower-moving outer region that emits the bulk of the observed radio emission [44]. This follows the same pattern as the transverse velocity structures, conjectured for FRI jets, that are thought to result from the entrainment of external material (see Section 4).

3.2. The dependence of beamed iC-CMB on beaming factors and redshift

In modelling beamed iC-CMB emission, most authors use the approximation that CMB photons, isotropic in the observer's frame, are scattered into directions in the jet frame that are parallel to the instantaneous velocity vectors of the scattering electrons (e.g. 58, 102). This has been shown to be an excellent approximation for calculating the X-ray emissivity as long as the jet's bulk motion has Lorentz factor 2 [59], which is, in any case, required for the mechanism to be effective at producing strong X-ray fluxes. The basic physics of the formalism is particularly clearly presented in [58], and here those formulae are presented in a slightly different form which is independent of the system of units.

We consider a source travelling at speed c and bulk Lorentz factor towards the observer at an angle to the line of sight, so that the bulk relativistic Doppler factor, , is given by

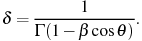(4)

An electron of Lorentz factor will scatter a CMB photon that has a characteristic frequency today of _CMB to an observed frequency, , given by

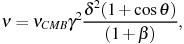(5)

where the spectral redistribution function is approximated as a delta function (equation (7) of [58], written in the notation of this paper). A delta-function approximation is also used for the synchrotron spectral distribution function such that an electron of Lorentz factor radiates at frequency

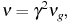(6)

where _g is the non-relativistic electron gyrofrequency, which is proportional to the magnetic field strength, B. Written in SI units, _g = eB / 2 m_e 30 B GHz, where B is in units of Tesla. For a CMB that is monochromatic at a frequency of _CMB at redshift equal to zero, then the ratio of inverse Compton to synchrotron flux density at a fixed frequency in the observer's frame is simply given by

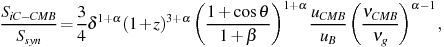(7)

where u_CMB is the energy-density of the CMB at a redshift of zero and u_B is the energy density in the magnetic field in the rest-frame of the jet. Noting that u_B B_int² and _g B_int, where B_int is the intrinsic magnetic-field strength in the rest-frame of the jet,

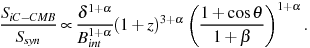(8)

If the modelling assumes minimum energy in relativistic particles and fields, then Equation 2 can be used. The luminosity density can be written in terms of the observable synchrotron flux density using

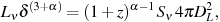(9)

where D_L is the luminosity distance. The volume of a radio source can be specified in terms of its angular component sizes, _x, _y and path length through the source, d, as

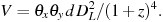(10)

Substituting for L and V (Equations 9 and 10) in Equation 2 then gives

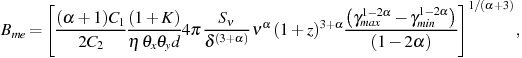(11)

i.e.,

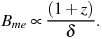(12)

Substituting for B_int = B_me in Equation 8 gives

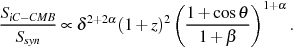(13)

Equation 9 (and thus Equations 11, 12 and 13) applies to a spherical blob in which S_syn ³⁺: for a continuous jet where S_syn ²⁺, B_me 1 / ^{(2+) / (3+)}, and Equation 13 has a slightly more complicated dependence on . Also, Equation 10 adopts the assumption that the pathlength through the jet is independent of redshift. Alternative assumptions could be adopted, modifying the redshift dependencies in Equations 11, 12 and 13.

3.3. How is the beamed iC-CMB model faring under scrutiny?

It was obvious that there were important consequences if the beamed iC-CMB interpretation of the X-ray emission from the resolved jet of PKS 0637-752 is correct, and holds for other quasar jets. In particular, increasing from the previously accepted value of ~ 2 to ~ 20 means increasing the jet power by a factor of ~ 100, or more if cold ions are an important contributor to the jet composition (see appendix B of [178]).

Programs targeting the resolved radio jets of core-dominated quasars with Chandra followed the work on PKS 0637-752 [170, 171, 141]. The detection success rate of roughly 50 per cent in relatively short exposures made it clear that PKS 0637-752 is not an outlier. Longer Chandra observations were made of some of the X-ray brightest and morphologically most interesting sources (e.g. 142, 169, 181, 182, 183, 115, 116, 178, 180, 179, 200). The combination of surveys and long pointed observations have made it possible to look critically at the application of the beamed iC-CMB model to these sources.

The high X-ray detection rate of quasar jets in short exposures is notable. In most Chandra observations of FRII radio galaxies at similar redshifts to the quasars, the jets (as opposed to the terminal hotspots) are not detected (e.g. 218, 12). This can be understood in the framework of quasar/radio-galaxy unification with reference to Figure 7 (based on Equation 8) which shows that for jets that are intrinsically the same, the ratio of beamed-iC to synchrotron radiation strongly decreases with increasing jet angle to the line of sight. The observed quasar X-ray jet emission is normally one-sided and on the same side as the brighter radio jet, in support of relativistic beaming. Where two-sided X-ray emission has been seen, explanations can be found which are not in violation of fast jet speeds (e.g. 71, 120).

Figure 7. Normalized ratio of inverse Compton to synchrotron flux density for a fixed intrinsic magnetic field strength for different jet angles to the line of sight. The normalization is to the value for a jet with a Lorentz factor of 15 and = 1.1 at 0° to the line of sight. Solid and dashed curves are for = 0.6 and = 1.1, respectively. Each set has curves for = 15, = 10, and = 5, in descending order at = 0°. Based on Equation 8.

In general the jets contain multiple knots that can be fitted independently to the beamed iC-CMB model with minimum-energy magnetic field strengths of order 10-20 µG (1-2 nT) (e.g. 178). Note, however, that there are insufficient observational constraints to fit the two free parameters of angle to the line of sight and bulk Lorentz factor separately, and an assumption must be made on one of these parameters. It has been common to assume sin = 1 / (i.e., = ), although this is not particularly sensible for sources where multiple knots in the same source give different values for , since it can lead to a jet that bends more erratically than makes physical sense. In some cases the results can be shown to agree with the estimates of speed and power from simple models for the pc-scale emission (e.g., 116, 200, and see Section 8.4), although with rather large uncertainties.

There is, however, a major difficulty with the beamed iC-CMB interpretation that arises from a detailed comparison between radio and X-ray emission. Figure 8 (based on Equation 5) shows the mean Lorentz factor of electrons that scatter photons from the peak of the CMB spectrum into the X-ray at 1 keV, for various jet bulk Lorentz factors and angles to the line of sight. The synchrotron emission from these electrons will be at a peak frequency of ² _g 30² B GHz, where _g is the gyrofrequency and B is magnetic field strength in Tesla. For a typical field of 2 nT, the radio synchrotron emission from these electrons is at 0.3 MHz if = 100, or 20 MHz if = 10³, both below the observable radio band. Under the beamed iC-CMB model, which requires small angle to the line of sight, , to be effective, the X-ray emission thus arises from lower-energy electrons than the radio emission. These electrons have long synchrotron energy-loss lifetimes. However, observations sometimes show X-ray emission that weakens relative to the radio towards the downstream regions of the jets and in some cases in individual knots, indicating that the population of low-energy electrons is being depleted more rapidly than the population of high-energy electrons, contrary to expectations based on radiation losses. This was seen in PKS 0637-752 ([177, 45], and see Fig. 9), and such behaviour is also seen strikingly in several other sources including 3C 273 [142, 169], quasar 0827+243 [115], PKS 1127-145 [181] and PKS 1136-135 [172]. Various suggestions have been made to overcome the problem within the framework of the beamed iC-CMB model, but none is uniformly regarded as satisfactory.

Figure 8. Mean Lorentz factor, , of electrons which scatter CMB photons near the black-body peak to X-ray photons of 1 keV. Results are shown for an emission region at selected angles to the line of sight over a range of bulk Lorentz factor, . Based on Equation 5.

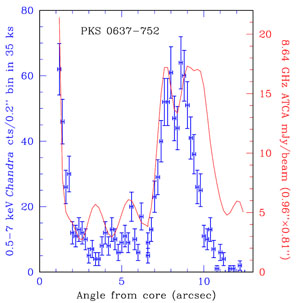Figure 9. The X-ray and radio profiles down the jet of PKS 0637-752 (see Fig 6). The X-ray intensity drops before the radio at large jet angles. 1" corresponds to a projected linear distance of 6.93 kpc.

It has been suggested that strong clumping in the jets may resolve the problem through adiabatic energy losses [198]. However, it is not clear that the beamed iC-CMB mechanism is then required, since such clumping would increase the SSC yield for a slow jet at minimum energy [177]. Alternatively, it has been suggested that jet deceleration is important, perhaps through entrainment of external gas (e.g. 81, 172, 199). A problem with this as a general solution is that, as shown in Figure 10 (based on Equations 8 and 13), the ratio of inverse Compton to synchrotron emission only falls for a decelerating jet over particular ranges of bulk Lorentz factor for jets at an angle of less than about 5° to the line of sight. This means that any source for which the X-ray drops off faster than the radio with downstream distance would need to be at particularly small angle to the line of sight or rather slow (but see [81] for a more detailed treatment that includes compression of the magnetic field and thus relative amplification of the radio synchrotron emission downstream). Jet deceleration is potentially testable through looking at the X-ray and radio profiles of source samples.

Figure 10. Normalized ratio of inverse Compton to synchrotron flux density for a fixed jet angle to the line of sight with decreasing Lorentz factor, . Left: with fixed intrinsic magnetic field. Right: with minimum-energy magnetic field. In each panel separately the curves are normalized to the value of SiC / Ssyn for a jet with a Lorentz factor of 15, = 1.1, at 5° to the line of sight. Solid and dashed curves are for = 0.6 and = 1.1, respectively. Each set has curves for = 5°, = 10°, and = 15°, in descending value on the y-axis at = 15.

A point in favour of the beamed iC-CMB explanation is that the particularly straight knotty jet in the quasar 4C 19.44 shows one of the most uniform X-ray to radio ratios over almost a dozen discrete knots in its straightest section ([179], and see Fig. 11). In contrast to PKS 0637-752, the radio drops more rapidly than the X-ray at the end of the straight, well-collimated jet beyond about 15" from the nucleus (Fig. 12). This might suggest that drops in the level of X-ray to radio emission along other jets are the result of the jets bending out of the line of sight. Since quasar jets are selected for observation based partly on their core radio emission, any bending downstream is more likely in a direction away from the line of sight than towards it. A large change in jet angle could easily produce the typical decreases in X-ray to radio ratio (a factor of a few to about 10; compare with Fig. 7). However, it is difficult to understand how a real change in angle of a ~ 20 flow by more than about a degree could occur without severe jet decollimation ². As apparent from Figure 7, more than a factor of about two decrease in X-ray to radio ratio is then not expected from bending alone.

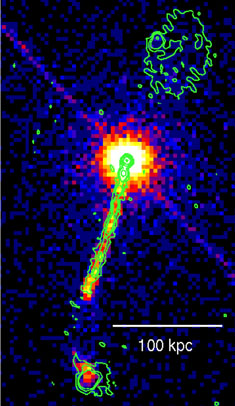Figure 11. The z = 0.72 quasar 4C 19.44, using data from [179]. The plot show an unsmoothed Chandra X-ray image of ~ 189.4 ks exposure with radio contours from a 4.86 GHz VLA radio map (beam size 0.47" × 0.43"). X-ray emission is detected from the nucleus, the southern radio jet, the northern hotspot and southern radio lobe. The excess X-ray counts in a line running NE-SW centred on the nucleus are a frame-readout artifact.

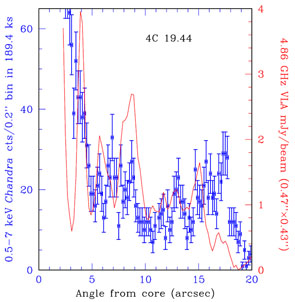Figure 12. The X-ray and radio profiles down the jet of 4C 19.44 (see Fig. 11). In contrast to PKS 0637-752 (Fig. 9), the radio intensity drops before the X-ray at large jet angles. 1" corresponds to a projected linear distance of 7.23 kpc.

A test that the beamed iC-CMB explanation must pass concerns the redshift dependency. The increase in CMB energy density with redshift means that the X-ray to radio ratio should increase with redshift by a factor of something like (1 + z)² (Equation 13: the precise dependence on redshift depends on assumptions concerning minimum energy and whether or not the path length through the source is redshift dependent). Such a redshift effect is not ruled out [141] although a larger sample is needed for a more definitive test.

3.4. Synchrotron emission as an alternative

The fast jet speed required for the beamed iC-CMB explanation of quasar X-ray emission disappears if an alternative explanation can be found for the X-rays. It is then natural to invoke synchrotron radiation, the mechanism producing the X-rays in low-power FRI jets (see Section 5.1). However, whereas for FRI jets the SED can normally be modelled with a broken power-law spectrum from the radio, through the optical to the X-ray (e.g. 29, 96, 21), PKS 0637-752 has too little optical emission to allow this, and a separate population of electrons with an anomalously high low-energy cutoff would be required [177]. Figure 13 compares the spectral distribution of the FRI radio galaxy M 87, where a broken-power-law synchrotron components fits well, with that of the FRII quasar PKS 0637-752.

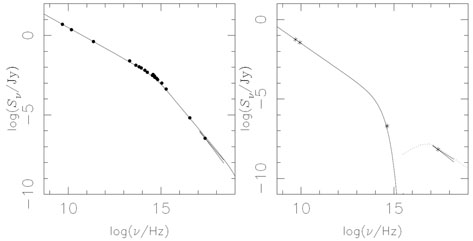Figure 13. Spectral distributions from the radio to X-ray. Left: The integrated emission from Knots A, B and C of M 87, using data from [28] and [13], fits a broken power law synchrotron spectrum, although the change of 1.5 in electron spectral slope is greater than expected from a simple model for synchrotron energy losses. Right: A broken power-law spectrum does not fit through the emission from Knot WK7.8 of PKS 0637-752 (taken from [45]) although a synchrotron component with an exponential cutoff and either a beamed iC-CMB component or a separate synchrotron component with an anomalously high low-energy cutoff can be made to fit the data.

Most of the several tens of current quasar X-ray jet detections were found through targeted Chandra programs to observe bright, prominent, one-sided radio jets. In most cases there was no pre-existing reported optical jet detection, but there has been reasonable success from follow-up work. The level of such optical detections often lies below an interpolation between the radio and X-ray spectra, supporting the idea that synchrotron emission from a single power-law distribution of electrons is not responsible for all the emission (e.g. 171).

However, the conclusion regarding synchrotron emission is not quite as clear cut, since a single-component electron spectrum will harden at high energies if inverse-Compton losses are also important (since this loss process is less efficient in the Klein-Nishina regime), and the consequent spectral hardening in the synchrotron spectrum might then better match observations [60].

As long as electrons can be accelerated to high energy (and they can be in FRIs) they will produce synchrotron radiation at some level. Radio galaxies are at large angle to the line of sight and any iC-CMB emission will be beamed out of the line of sight of the observer (an extension of to large angle shows that, even for the most optimistic case, the ratio of iC-CMB to synchrotron emission drops three orders of magnitude between = 0 and = 80°). Indeed, synchrotron X-ray emission from knots in the radio jets of nearby FRII radio galaxies is reported (e.g. 212, 219, 125, 120). When optical detections are also available, the energy distributions [125, 219] are of similar simple form to those in FRIs (see Fig. 14), not requiring the complex electron spectral forms generally needed to explain quasar X-ray emission as synchrotron radiation. Spatial offsets reminiscent of those seen in FRIs and which are presumably a feature of the particle acceleration processes (see Section 5.2) are also seen [219, 120].

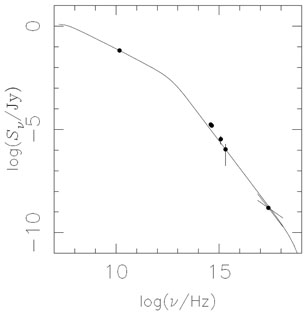Figure 14. The spectrum from the radio to X-ray for the knot in the FRII radio galaxy 3C 346 (see Fig. 16) fits a broken-power-law synchrotron model.

It remains uncertain as to whether or not in quasars it is necessary to explain the jet X-ray emission as the synchrotron output of a distorted electron spectrum [60] or from separate populations of electrons (e.g. 7), as an alternative to the beamed iC-CMB model. In the case of 3C 273, the run of X-ray spectral slope down the jet rules out a simple beamed iC-CMB interpretation, but a two-zone iC-CMB model with a faster spine, although disfavoured, cannot be ruled out ([112]). If a synchrotron interpretation is sought, similar, simple electron spectra in all jet regions do not fit observations (e.g. 166, 169, 142). A two-zone model with faster spine has been proposed, where, unlike for beamed iC-CMB in which the X-rays are from the spine, the X-rays would arise from the shear layer through electron acceleration to very high energy [112].

It is important to understand the primary X-ray emission in quasar jets, and this remains an observational problem - more work on samples and further detailed, deep, multiwavelength observations of individual sources are needed. Predictions for yields at higher energies also differ according to the X-ray emission mechanism, and so there is a prospect that the new Fermi Gamma-ray Space Telescope will help in finding solutions (e.g. 60, 83). Optical polarimetry is potentially a strong discriminant since, unlike for optical synchrotron emission, the optical emission should be essentially unpolarized if it is a lower-energy extension of X-ray emission that is produced via the beamed iC-CMB mechanism (e.g. 113, 203).

² Large changes in jet angle in projection are observed in many sources, but Figure 7 relates to the true jet angle to the line of sight. Back.