Annu. Rev. Astron. Astrophys. 2010. 48: 673-710 Copyright © 2010 by Annual Reviews. All rights reserved

5. OTHER METHODS FOR DETERMINING H_o

Although the focus of this review is the determination of H_o and the extragalactic distance scale, we briefly mention two indirect techniques that probe great cosmological distances independently: gravitational lensing and the Sunyaev-Zel'dovich effect. We also discuss measurements of anisotropies in the cosmic microwave background, which offer a measurement of H₀, in combination with other data.

5.1. Gravitational Lens Time Delays and H_o

As first realized by Refsdal (1964), measurements of the differences in arrival time, coupled with measurements of the angular separation of strongly lensed images of a time-variable object (such as a quasar or supernova) can be used to measure H_o. The time delay observed between multiple images is proportional to H_o ^-1, and is less dependent on other cosmological parameters such as _matter and . An extensive review of the physics of lensing can be found in Blandford & Narayan (1986); the observational issues have been summarized nicely by Myers (1999) and Schechter (2005).

Initially, the practical implementation of this method suffered from a number of difficulties. Time delays have proven difficult to measure accurately, the amplitude of quasar variability is generally small, and relatively few lens systems that can be modeled simply and cleanly have been found. Dust obscuration is an issue at optical wavelengths. A great challenge of this method is that astronomical lenses are galaxies whose underlying mass distributions are not known, and a strong physical degeneracy exists between the mass distribution of the lens and the value of H_o. As emphasized by Gorenstein, Shapiro & Falco (1988), the deflections and distortions do not uniquely determine the mass distribution: a lens may be located in a group(s) or cluster(s), which will affect the predicted time delays, an effect termed the mass sheet degeneracy. Measurements of velocity dispersion as a function of position can be used to constrain the mass distribution of the lens, but generally only central velocity dispersion measurements are feasible. An advantage of the method is that it offers a probe directly at cosmological distances; the concomittent disadvantage is that the cosmological model must be assumed in order to determine H_o. Earlier estimates of H_o using this technique yielded values about 10% lower (analyzing the same data), assuming what was then the standard cosmological model with _matter = 1.0, in comparison to the current standard model with _matter = 0.3 and = 0.7.

The precision and accuracy of this technique has continued to improve over time. A brief survey of results from gravitational lensing over the past five years can be found in Suyu et al. (2009), with estimates of H_o in the range 50 to 85 km s^-1 Mpc^-1. There is a wide range in types of modeling and treatment of errors for these different systems (e.g., assumed isothermal profiles, assumptions about the density distribution of the environment, and how well the models are constrained by the data).

A recent extensive analysis of the quadruple lens system B1608+656 has been carried out by Suyu et al. (2009). This analysis is based on deep F606W and F814W ACS data, a more accurate measurement of the velocity dispersion using the Low-Resolution Imaging Spectrometer (LRIS) on Keck, a more detailed treatment of the lens environment using a combination of ray tracing through cosmological N-body simulations (the Millennium Simulation) along with number counts in the field of

B1608+656, in order to help break the mass sheet degeneracy problem. Adopting the standard cosmological model with _matter = 0.3, = 0.7, and w = -1, they find H_o = 71 ± 3 km s^-1 Mpc^-1, a factor of two improvement over the previous estimate for this lens.

5.2. The Sunyaev-Zel'dovich (SZ) Effect and H_o

Sunyaev & Zel'dovich (1969) described the inverse-Compton scattering of photons from the cosmic microwave background (CMB) off of hot electrons in the X-ray gas of rich clusters of galaxies. This scattering leads to a redistribution of the CMB photons so that a fraction of the photons move from the Rayleigh-Jeans to the Wien side of the blackbody spectrum, referred to as the Sunyaev-Zel'dovich (SZ) effect. The measured effect amounts to about 1 mK. The Hubble constant is obtained using the fact that the measured X-ray flux from a cluster is distance-dependent, whereas the SZ decrement is essentially independent of distance. Observations of this effect have improved enormously in recent years, with high signal-to-noise, high angular resolution, SZ images obtained with ground-based interferometric arrays and high-resolution X-ray spectra. The theory of the SZ effect is covered at length by Birkinshaw (1999); a nice summary of observational techniques and interferometry results is given in Carlstrom et al. (2002).

The SZ effect is proportional to the first power of the electron density, n_e: T_SZ ~ dl n_e T_e, where T_e is the electron temperature, and dl is the path length along the line-of-sight, related to the angular diameter distance. The X-ray emission is proportional to the second power of the density: S_x ~ dl n_e², where is the cooling function for the X-ray gas. The angular diameter distance is solved for by eliminating the electron density (see Carlstrom et al. 2002; Birkinshaw 1999).

An advantage of this method is that it can be applied at cosmological distances, well into the Hubble flow. The main uncertainties result from potential substructure in the gas of the cluster (which has the effect of reducing H_o), projection effects (if the clusters observed are prolate, the sense of the effect is to increase H_o), the assumption of hydrostatic equilibrium, details of the models for the gas and electron densities, and potential contamination from point sources.

The accuracy of this technique has continued to improve as interferometric radio observations (e.g., Berkeley-Illinois-Maryland Association, BIMA and Owens Valley Radio Observatory, OVRO) and ROSAT and now Chandra X-ray data have become available. In a recent study by Bonamente et al. (2006), new Chandra X-ray measurements for 38 clusters in the redshift range 0.14 < z < 0.89 have been obtained. Combining these data with BIMA and OVRO data for these same clusters, and performing a Markov Chain Monte Carlo analysis, these authors find a value of H_o = 76.9_{-3.4 -8.0}^{+3.9 +10.0} km s^-1 Mpc^-1, under the assumption of hydrostatic equilibrium. Relaxing the assumption of hydrostatic equilibrium, and adopting an isothermal model, they find H_o = 73.7_{-3.8 -7.6}^{+4.6 +9.5} km s^-1 Mpc^-1.

5.3. Measurements of Anisotropies in the Cosmic Microwave Background

The prediction of acoustic oscillations in the cosmic microwave background radiation (Peebles & Yu 1970; Sunyaev & Zel'dovich 1970) and the subsequent measurement of these peaks (culminating most recently in the five (Dunkley et al. 2009) and seven-year (Bennett et al. 2010) measurements of WMAP, the Wilkinson Microwave Anisotropy Probe) is one of the most successful chapters in the history of cosmology. A recent detailed review of the cosmic microwave background is given in Hu & Dodelson (2002). The aim in this section is simply to elucidate the importance of accurate measurements of the Hubble constant in the context of measurements of the angular power spectrum of CMB anisotropies, and the complementary nature of the constraints provided.

The temperature correlations in the maps of the CMB can be described by a set of spherical harmonics. A plot of the angular power spectrum as a function of multipole moment, l, is shown in Figure 11. This spectrum can be naturally explained as a result of the tight coupling between photons and baryons before recombination (where electrons and protons combine to form neutral hydrogen), and a series of oscillations are set up as gravity and radiation pressure act on the cold dark matter and baryons. After recombination, photons free-stream toward us. The position of the first peak in this diagram is a projection of the sound horizon at the time of recombination, and occurs at a scale of about 1 degree.

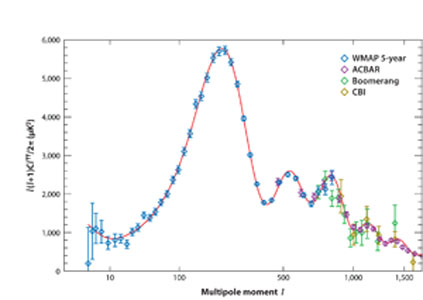Figure 11. The WMAP 5-year "temperature angular power spectrum" (Nolta et al. 2009) incorporating other recent results from the ACBAR (Reichardt et al. 2008, purple), Boomerang (Jones et al. 2006, green), and CBI (Readhead et al. 2004, red) experiments. The red curve is the best-fit CDM model to the WMAP data.

Although measurements of the CMB power spectrum can be made to very high statistical precision, there are some nearly exact degeneracies that limit the accuracy with which cosmological parameters can be estimated (e.g., Efstathiou & Bond 1999). These degeneracies impose severe limitations on estimates of curvature and the Hubble constant derived from CMB anisotropy alone, and are sometimes overlooked. Specifically, the value of H_o is degenerate with the value of and w. Different combinations of the matter and energy densities and H_o can produce identical CMB anisotropy spectra. Alternatively, an accurate independent measurement of H_o provides a means of constraining the values of other cosmological parameters based on CMB anisotropy data.

The WMAP data provide strong evidence for the current standard cosmological model with _matter = 0.23, = 0.73 (Spergel et al. 2003; Komatsu et al. 2010). A prior on H_o can help to break some of the degeneracies in the CMB data. The WMAP data measure _matter h²; assuming a flat universe, yields a stronger constraint on the equation of state, -0.47 , w < 0.42 (95% CL) (Komatsu et al. 2009) than WMAP data alone. Alternatively, combining the WMAP-5 data with SNe Ia and BAO data yields a value of H₀ = 70.5 ± 1.3 km s^-1 Mpc^-1 (Komatsu et al. 2009), still in excellent agreement with other methods.

5.3.1. MEASUREMENTS OF BARYON ACOUSTIC OSCILLATIONS IN THE MATTER POWER SPECTRUM    Baryon acoustic oscillations (BAO) arise for the same underlying physical reason as the peaks and valleys in the cosmic microwave background spectrum: the sound waves that are excited in the hot plasma owing to the competing effects of radiation pressure and gravity at the surface of last scattering also leave an imprint on the galaxy matter power spectrum. The two-point correlation function has a peak on scales of 100 h^-1 Mpc (Eisenstein et al. 2005), which provides a "standard ruler" for measuring the ratio of distances between the surface of last scattering of the CMB (at z = 1089) and a given redshift. Measurement of BAO in the matter power spectrum can also help to break degeneracies in the CMB measurements. For example, Percival et al. (2009) have combined the Sloan Digital Sky Survey (SDSS) 7th data release with the Two-degree Field Galaxy Redshift Survey (2dFGRS) to measure fluctuations in the matter power spectrum at six redshift slices. For CDM models, combining these results with constraints for the baryon and cold dark matter densities, _b h², and _CDM h² from WMAP 5, and data for SNe Ia, yields _matter = 0.29 ± 0.02 and H_o = 68 ± 2 km s^-1 Mpc^-1.