Copyright © 2010 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2010. 48:
673-710 Copyright © 2010 by Annual Reviews. All rights reserved |
There are three independent ways of determining the age of the Universe. The first is based on an assumed cosmological model and the current expansion rate of the Universe. The second is based on models of stellar evolution applied to the oldest stars in the Universe. The third is based on measurements of the angular power spectrum of temperature fluctuations in the CMB. All three methods are completely independent of each other, and so offer an important consistency check. The kinematic age of the Universe is governed by the rate at which the Universe is currently expanding, modified by the combined extent to which gravity slows the expansion and dark energy causes it to accelerate.
The time back to the Big Bang singularity depends upon Ho and the expansion history, which itself depends upon the composition of the universe:
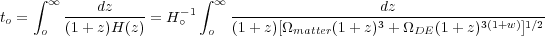 |
(14) |
For a matter-dominated flat universe with no dark energy
( matter =
1.0,
matter =
1.0,
 vacuum =
0.0, the age is simply
2/3 of the Hubble time, or only 9.3 billion years for h = 0.7.
vacuum =
0.0, the age is simply
2/3 of the Hubble time, or only 9.3 billion years for h = 0.7.
Not accounting for the presence of dark energy in the Universe leads
to an underestimate of its age. Before the discovery of dark energy,
an "age controversy" persisted for several decades: values of the
Hubble constant any larger than 40-50 km s-1 Mpc-1
appeared to yield ages for the universe as a whole that were smaller than
stellar evolution calibrated ages of the oldest stars in the Milky
Way. For a universe with a Hubble constant of 73 km sec-1
Mpc-1, with
 matter =
0.27 and
matter =
0.27 and
 vacuum =
0.73, the age is 13.3 Gyr. Taking account of the systematic
uncertainties in Ho alone, the uncertainty in the age
of the Universe is estimated to be about ± 0.8 Gyr.
vacuum =
0.73, the age is 13.3 Gyr. Taking account of the systematic
uncertainties in Ho alone, the uncertainty in the age
of the Universe is estimated to be about ± 0.8 Gyr.
The most well-developed of the stellar chronometers employs the oldest stars in globular clusters in the Milky Way (Krauss & Chaboyer 2003). The largest uncertainty for this technique comes from determination of the distances to the globular clusters. Recent, detailed stellar evolution models when compared to observations of globular clusters stars, yield a lower limit to their ages of 10.4 billion years (at the 95% confidence level) with a best-fit age of 12.6 Gyr. Deriving the age for the Universe from the lower limit requires allowing for additional time to form the globular clusters: from theoretical considerations this is estimated to be about 0.8 billion years. This age estimate for the Universe agrees well with the expansion age. Two other stellar chronometers: the cooling of the oldest white dwarf stars (for a recent review see Moehler & Bono 2008) and nucleocosmochronology, the decay of radioactive isotopes (Sneden et al. 2001), yield similar ages.
The expansion age can also be determined from measurements of the CMB
anisotropy. Ho cannot be measured directly from the
CMB alone,
but the heights of the peaks in the CMB spectrum provide a constraint
on the product
 matter
Ho2, and the position of the
peaks constrain the distance to the last-scattering surface. Assuming
a flat universe yields a consistent age, to = 13.7
± 0.13 Gyr
(Spergel et al. 2003;
Komatsu et al. 2009),
again in good agreement with the other two techniques.
matter
Ho2, and the position of the
peaks constrain the distance to the last-scattering surface. Assuming
a flat universe yields a consistent age, to = 13.7
± 0.13 Gyr
(Spergel et al. 2003;
Komatsu et al. 2009),
again in good agreement with the other two techniques.
In summary, several methods of estimating the age of the universe are now in good agreement, to within their quoted uncertainties, with a value to = 13.7 ± 0.5 Gyr.