Galaxy clusters are the largest gravitationally bound objects in the
universe. They are also among the rarest objects in the universe. While
these two facts about galaxy clusters may seem disparate, they are in
fact intimately related. Our current theory of the origin and evolution
of galaxy clusters places them within the broader context of
cosmological structure formation in which galaxies, galaxy groups,
galaxy clusters, and galaxy superclusters all arise from gravitational
instability amplifying perturbations in the cold dark matter density
field in an expanding universe. At early times the perturbations are
linear in amplitude, and are extremely well described by a Gaussian
random field with a known power spectrum (the
CDM power
spectrum; cf. Fig. 2).
At later times, density perturbations become nonlinear and collapse into
gravitationally bound systems. The shape of the
CDM power
spectrum is such
that structure forms from the "bottom up", with galaxies forming
first and clusters forming later. It just so happens that we live in a
universe in which cluster-scale perturbations collapsed rather recently
(since z ~ 1), which accounts for their rarity as well as
their sometimes complex substructure.
As cluster-scale perturbations collapse, they bring in all matter within
a sphere of comoving radius of about 15 Mpc, which includes galaxies,
intergalactic gas, and anything else in that patch of the
universe. Because the escape velocity of galaxy clusters is of order
1000 km/s, everything but relativistic particles become trapped in the
cluster potential well. For this reason it is often said that clusters
represent a fair sample of the universe. This is true from the
standpoint of their matter content. However, from the standpoint of
cosmological structure this could not be further from the truth. Galaxy
clusters form and evolve in the rarest peaks (~
3
) of the
density field (Fig. 1). Galaxy formation begins
sooner in such regions, and the galaxies evolve due to internal and
external processes which are somewhat different from the general field
(e.g., ram pressure stripping).
 |
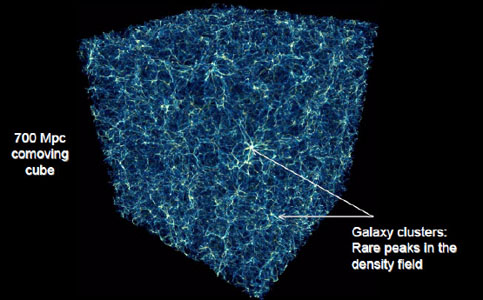Figure 1. AMR hydrodynamic cosmological simulation of cosmic structure in a 700 Mpc volume of the universe. Up to seven levels of adaptive mesh refinement (AMR) resolve the distribution of baryons within and between galaxy clusters, for an effective resolution of 65,5363. Volume rendering of baryon density. From [70]. |
Galaxy clusters are interesting objects in their own right, and for decades have been extensively studied in the optical, Xray, and radio wavebands [65]. More recently this has been extended to the microwave, infrared, and extreme UV [66, 67], motivated in part by the fact that galaxy clusters are excellent cosmological probes. Because of their large size and high X-ray luminosities, they can be seen to great distances. As discussed in this volume and in [67], galaxy clusters can also be seen in absorption/emission against the cosmic microwave background (CMB) via the Sunyaev-Zeldovich effect (SZE). As discussed by Rephaeli elsewhere in these proceedings, the SZE is redshift independent, meaning that deep microwave surveys should detect all galaxy clusters in a particular region of the sky regardless of their redshift provided the telescope has enough angular resolution and sensitivity. Indeed such surveys are underway now and results are expected soon.
One of the most challenging measurements in modern observational
cosmology is the dark energy equation of state which describes
the time rate of change of the vacuum energy
density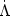 
responsible for the accelerating expansion of the universe
[5].
Galaxy clusters were identified by the US Dark Energy Task Force
(DETF) as one of four complementary methods for doing this. However in
order to measure
we must
measure the cluster mass distribution function
versus redshift to very high accuracy.
Accurately measuring the mass of a galaxy cluster is actually quite
difficult despite the number of ingenious techniques that have been
developed. This motivates attempts to measure the "mass-observable"
relationships in observed samples of clusters, and find the ones with
the least scatter and least bias.
Numerical simulations are helpful in this regard, as one can in principle calibrate the mass-observable relationships by comparing simulated observations with in situ measurements. Where this has been done, a discouraging result is found: most of the observables of a given simulated cluster depend sensitively on numerical resolution and assumed baryonic physics, including radiative cooling, star formation, galactic and AGN feedback processes. However it has been shown that the integrated SZE signal is rather insensitive to assumed baryonic physics [48, 71], perhaps relaxing requirements on modelers and giving encouragement to SZE cluster observers that the dark energy program may be feasible after all. The point is that the astrophysics of galaxy clusters and their utility as cosmological probes are inextricably linked, and both are worthwhile of study.
I was asked by the organizers to lecture on three topics relavant to the theme of the summer school. First I was asked to review the standard cosmological framework and basic results from the theory of cosmological structure formation within which galaxy clusters can be understood. Second, I was asked to review how galaxy clusters are simulated on a computer, and summarize the basic findings. I do this in the next two sections, which are slightly updated and abbreviated versions of the lecture notes I published in the 2004 Varenna Summer School volume [67]. Finally I was asked to give a lecture of my choosing, which was on recent progress in galaxy cluster modeling focusing on the incorporation of additional baryonic physics and simulating SZE surveys . These topics are presented in Sections 5 and 6 respectively.
In line with the character of the summer school, I have attempted to be pedagogical, emphasizing the key concepts and results that a student needs to know if s/he wants to understand the current literature or do research in this area. Literature citations are kept to a minimum, except for textbooks, reviews, and research papers that I found to be particularly helpful in preparing this article. I am indebted to Dr. Rocky Kolb whose slides much of Section 2 are based upon.