

1.1. The Jeans mass and the filter mass
In the currently dominant
 CDM paradigm,
gravitationally
bound objects form in a hierarchical fashion, with the smallest, least
massive objects forming first, and larger objects forming later through
a mixture of mergers and accretion. The mass scale of the least massive
objects to form from dark matter is set by free-streaming of the dark matter
particles, and so depends on the nature of these particles. However, in
most models, this minimum mass is many orders of magnitude smaller
than the mass of even the smallest dwarf galaxies
(Green, Hofmann &
Schwarz 2005).
More relevant for the formation of the first stars and galaxies is the mass
scale of the structures (frequently referred to as dark matter 'minihalos')
within which the baryonic component of matter, the gas, can first cool and
collapse.
CDM paradigm,
gravitationally
bound objects form in a hierarchical fashion, with the smallest, least
massive objects forming first, and larger objects forming later through
a mixture of mergers and accretion. The mass scale of the least massive
objects to form from dark matter is set by free-streaming of the dark matter
particles, and so depends on the nature of these particles. However, in
most models, this minimum mass is many orders of magnitude smaller
than the mass of even the smallest dwarf galaxies
(Green, Hofmann &
Schwarz 2005).
More relevant for the formation of the first stars and galaxies is the mass
scale of the structures (frequently referred to as dark matter 'minihalos')
within which the baryonic component of matter, the gas, can first cool and
collapse.
A lower limit on this mass scale comes from the theory of the growth of small density perturbations in an expanding universe (see e.g. Barkana & Loeb 2001). From the analysis of the linearized equations of motion, one can identify a critical length scale, termed the Jeans length, that marks the boundary between gravitationally Jeans length stable and gravitationally unstable regimes. The Jeans length is given (in physical units) by
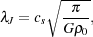 |
(1) |
where cs is the sound speed in the unperturbed
intergalactic medium and
 0
is the cosmological background density. Perturbations on scales
0
is the cosmological background density. Perturbations on scales
 >
>
 J are able
to grow under the influence of their own self-gravity, while those with
J are able
to grow under the influence of their own self-gravity, while those with
 <
<
 J are
prevented from growing by thermal pressure. We can associate a mass
scale with
J are
prevented from growing by thermal pressure. We can associate a mass
scale with  J
by simply taking the mass within a sphere of radius
J
by simply taking the mass within a sphere of radius
 J / 2
(Barkana & Loeb
2001):
J / 2
(Barkana & Loeb
2001):
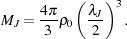 |
(2) |
This mass, termed the Jeans mass, describes the minimum mass that a perturbation must have in order to be gravitationally unstable.
In the simplest version of this analysis, the value used for the sound
speed in the equations for the Jeans length and Jeans mass is the
instantaneous value; i.e. to determine
 J and
MJ at a redshift z, we use the value of
cs at that redshift. In this approximation, the Jeans
mass is given in the high redshift limit (where the gas temperature is
strongly coupled to the cosmic microwave background [CMB] temperature by
Compton scattering) by the expression
(Barkana & Loeb
2001)
J and
MJ at a redshift z, we use the value of
cs at that redshift. In this approximation, the Jeans
mass is given in the high redshift limit (where the gas temperature is
strongly coupled to the cosmic microwave background [CMB] temperature by
Compton scattering) by the expression
(Barkana & Loeb
2001)
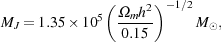 |
(3) |
where  m
is the dimensionless cosmological matter density parameter, and
h is the value of the Hubble constant in units of 100 km
s-1 Mpc-1.
In the low redshift limit (where the coupling between radiation and
matter is weak and the gas temperature evolves adiabatically), the Jeans
mass is given instead by
m
is the dimensionless cosmological matter density parameter, and
h is the value of the Hubble constant in units of 100 km
s-1 Mpc-1.
In the low redshift limit (where the coupling between radiation and
matter is weak and the gas temperature evolves adiabatically), the Jeans
mass is given instead by
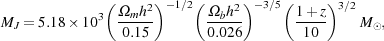 |
(4) |
where  b
is the dimensionless cosmological baryon density parameter.
The evolution of MJ with redshift is also illustrated
in Figure 1.
b
is the dimensionless cosmological baryon density parameter.
The evolution of MJ with redshift is also illustrated
in Figure 1.
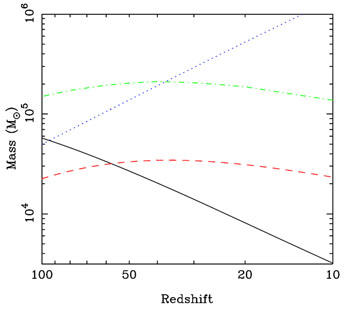 |
Figure 1. Evolution with redshift of the
Jeans mass (solid line), the filter mass computed in the limit where
the relative streaming velocity between gas and dark matter is zero
(dashed line) and the filter mass computed assuming a streaming
velocity v =
|
A more careful treatment of the growth of linear density perturbations accounts for the fact that the sound speed, the Jeans length and potentially also the Jeans mass may all change Jeans length Jeans mass significantly during the time it takes for a perturbation to grow into the non-linear regime. Gnedin & Hui (1998) showed that in this case, the appropriate mass scale separating the gravitationally stable and gravitationally unstable regimes is a form of time-averaged Jeans mass that they denote as the "filter mass", MF. This is given in physical units by
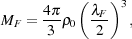 |
(5) |
where the filter wavelength
 F is given
in the high redshift limit by
Gnedin (2000)
F is given
in the high redshift limit by
Gnedin (2000)
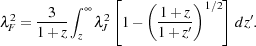 |
(6) |
It is possible to improve further on this analysis by accounting for spatial variations in the sound speed (Barkana & Loeb 2005, Naoz & Barkana 2005) and by properly accounting for the separate rates of growth of the dark matter and baryonic perturbations in the high redshift limit in which the gas is mechanically coupled to the CMB by Compton scattering (Naoz & Barkana 22007). The net result is to somewhat lower the filter mass in comparison with the predictions of Equations 5-6. Comparing the resulting filter mass with the Jeans mass (Figure 1), we see that the filter mass can be a factor of a few smaller than the Jeans mass at high redshift, but that for redshifts below z ~ 50, Jeans mass the filter mass is the larger of the two mass scales.
Another complication was recently pointed out by
Tseliakhovich &
Hirata (2010).
They show that prior to the recombination epoch, the strong coupling
between gas and radiation leads to the gas developing a non-zero
velocity relative to the dark matter. While the
gas and radiation are coupled, the sound-speed in the gas is approximately
c / 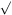 3, where
c is the speed of light, and the relative velocity between gas
and dark matter is highly subsonic. Once the gas and radiation decouple,
however, the sound-speed of the gas decreases enormously, becoming ~ 6 km
s-1 at the end of the recombination epoch.
Tseliakhovich &
Hirata (2010)
show that at the same
time, the RMS velocity of the gas relative to the dark matter is about 30
km s-1, implying that the gas is moving supersonically with
respect to the dark matter. The coherence length of the supersonic flow
is of the order of the Silk damping scale
(Silk 1968),
i.e. several comoving Mpc, and so on the much smaller
scales corresponding to the formation of the first star-forming
minihalos, the gas can be treated as being in uniform motion with
respect to the dark matter.
Tseliakhovich &
Hirata (2010)
also show that the relative velocity between gas and dark matter acts to
suppress the growth of small-scale structure in both components, and
that because this effect is formally a second-order term in cosmological
perturbation theory, it was not included in previous studies based on
linear perturbation theory.
3, where
c is the speed of light, and the relative velocity between gas
and dark matter is highly subsonic. Once the gas and radiation decouple,
however, the sound-speed of the gas decreases enormously, becoming ~ 6 km
s-1 at the end of the recombination epoch.
Tseliakhovich &
Hirata (2010)
show that at the same
time, the RMS velocity of the gas relative to the dark matter is about 30
km s-1, implying that the gas is moving supersonically with
respect to the dark matter. The coherence length of the supersonic flow
is of the order of the Silk damping scale
(Silk 1968),
i.e. several comoving Mpc, and so on the much smaller
scales corresponding to the formation of the first star-forming
minihalos, the gas can be treated as being in uniform motion with
respect to the dark matter.
Tseliakhovich &
Hirata (2010)
also show that the relative velocity between gas and dark matter acts to
suppress the growth of small-scale structure in both components, and
that because this effect is formally a second-order term in cosmological
perturbation theory, it was not included in previous studies based on
linear perturbation theory.
In a follow-up study,
Tseliakhovich, Barkana
& Hirata (2011)
improve on the
Tseliakhovich &
Hirata (2010)
analysis by accounting for spatial variations in the sound speed, and
study the effect that the relative velocity between the gas and the dark
matter has on the size of the filter mass. The magnitude of the relative
velocity v is randomly distributed with a Gaussian probability
distribution function (PDF) with total variance
 vbc2, i.e.
vbc2, i.e.
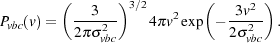 |
(7) |
Tseliakhovich, Barkana
& Hirata (2011)
show that for a relative velocity v =
 vbc (i.e. a one
sigma perturbation), the effect of the relative velocity between gas and
dark matter is to increase MF by roughly an order of
magnitude, as illustrated in
Figure 1. Higher sigma perturbations lead to
even greater increases in MF, but
Tseliakhovich, Barkana
& Hirata (2011)
show that the global average case (obtained by computing
MF for a range of different v and then
integrating over the PDF given in
Equation 7) is very similar to the one sigma case. Numerical studies of the
effects of these streaming velocities (see e.g.
Stacy, Bromm & Loeb
2011,
Greif et al. 2011b)
have generally confirmed this result,
although these studies still disagree somewhat regarding the influence
of the streaming velocities on minihalos with masses greater than the
revised MF.
vbc (i.e. a one
sigma perturbation), the effect of the relative velocity between gas and
dark matter is to increase MF by roughly an order of
magnitude, as illustrated in
Figure 1. Higher sigma perturbations lead to
even greater increases in MF, but
Tseliakhovich, Barkana
& Hirata (2011)
show that the global average case (obtained by computing
MF for a range of different v and then
integrating over the PDF given in
Equation 7) is very similar to the one sigma case. Numerical studies of the
effects of these streaming velocities (see e.g.
Stacy, Bromm & Loeb
2011,
Greif et al. 2011b)
have generally confirmed this result,
although these studies still disagree somewhat regarding the influence
of the streaming velocities on minihalos with masses greater than the
revised MF.
Nevertheless, even the most careful version of this analysis only tells us the mass scale of the first gravitationally bound structures to have a significant gas content, which is merely a lower limit on the mass scale of the first star-forming minihalos. The reason for this is that for stars to form within a minihalo, it is not enough that the gas be gravitationally bound; it must also be able to cool efficiently. In order for the gas within a minihalo to dissipate a large fraction of its gravitational binding energy - a necessary condition if pressure forces are not to halt the gravitational collapse of the gas (Hoyle 1953, Rees 1976, Rees & Ostriker 1977) - it must be able to radiate this energy away. The timescale over which this occurs is known as the cooling time, and is defined as cooling time
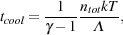 |
(8) |
where ntot is the total number density of particles,
 is the
adiabatic
index, k is Boltzmann's constant, T is the gas temperature
and
is the
adiabatic
index, k is Boltzmann's constant, T is the gas temperature
and  is the
radiative cooling rate per unit volume. If the cooling
time of the gas is longer than the Hubble time, then it is very unlikely
that the minihalo will survive as an isolated object for long enough to
form stars. Instead, it is far more likely that it will undergo a major
merger with another dark matter halo of comparable or larger mass before
any of its gas has cooled significantly, since major mergers occur, on
average, approximately once per Hubble time
(Lacey & Cole 1993).
Therefore, to determine the minimum mass of a star-forming minihalo, we
must first understand how cooling occurs within primordial gas, a topic
that we explore in the next section.
is the
radiative cooling rate per unit volume. If the cooling
time of the gas is longer than the Hubble time, then it is very unlikely
that the minihalo will survive as an isolated object for long enough to
form stars. Instead, it is far more likely that it will undergo a major
merger with another dark matter halo of comparable or larger mass before
any of its gas has cooled significantly, since major mergers occur, on
average, approximately once per Hubble time
(Lacey & Cole 1993).
Therefore, to determine the minimum mass of a star-forming minihalo, we
must first understand how cooling occurs within primordial gas, a topic
that we explore in the next section.
1.2. Cooling and chemistry in primordial gas
At high temperatures (T ~ 104 K and above), primordial gas can cool efficiently through the collisional excitation of excited electronic states of atomic hydrogen, atomic helium, and singly-ionized helium. However, it is relatively easy to show that most of the gas within a minihalo with M ~ MF will have a temperature significantly below 104 K. If we assume that the gas within the minihalo relaxes into a state of virial equilibrium, such that the total potential energy W and total kinetic energy K are related by W = - 2K, then we can use this fact to define a virial temperature for the minihalo (Barkana & Loeb 2001) virial temperature
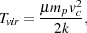 |
(9) |
where µ is the mean molecular weight, mp is the proton mass, and vc is the circular velocity of the minihalo. This can be rewritten in terms of the redshift z and the mass M of the minihalo as
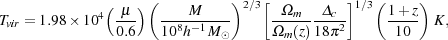 |
(10) |
where
 m(z)
is the dimensionless cosmological density parameter evaluated at
redshift z and
m(z)
is the dimensionless cosmological density parameter evaluated at
redshift z and
 c =
18
c =
18  2 + 82 d
- 39 d2, with d =
2 + 82 d
- 39 d2, with d =
 m(z)
- 1
(Bryan & Norman
1998).
In the standard
m(z)
- 1
(Bryan & Norman
1998).
In the standard
 CDM cosmology,
CDM cosmology,
 m(z)
m(z)
 1 at
z > 6, and hence the term in square brackets reduces to
1 at
z > 6, and hence the term in square brackets reduces to
 m1/3. If we rearrange
Equation 10 and solve for the mass Matom of a cloud
that has a virial temperature
Tvir = 104 K and that can therefore
cool via atomic excitation, we find that
m1/3. If we rearrange
Equation 10 and solve for the mass Matom of a cloud
that has a virial temperature
Tvir = 104 K and that can therefore
cool via atomic excitation, we find that
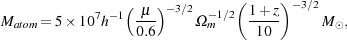 |
(11) |
significantly larger than our estimates for MJ and MF above. Minihalos with masses close to MJ or MF will therefore have virial temperatures much less than 104 K, placing them in the regime where molecular coolants dominate.
In primordial gas, by far the most abundant and hence most important molecule is molecular hydrogen, H2. The chemistry of H2 in primordial gas has been reviewed in a number of different studies (see e.g. Abel et al. 1997, Galli & Palla 1998, Stancil, Lepp & Dalgarno 1998, Glover & Abel 2008), and so we only briefly discuss it here. Direct formation of H2 by the radiative association of two hydrogen atoms is highly forbidden (Gould & Salpeter 1963), and so at low densities, most H2 forms via the reaction chain (McDowell 1961, Peebles & Dicke 1968)
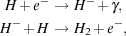 |
(12) (13) |
with a minor fraction forming via the reaction chain Saslaw & Zipoy 1967)
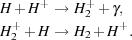 |
(14) (15) |
In warm gas, H2 can be destroyed by collisional dissociation (see e.g. Martin, Keogh & Mandy 1998)
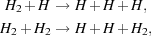 |
(16) (17) |
or by charge transfer with H+ (see e.g. Savin et al. 2004)
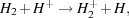 |
(18) |
but at low temperatures there are no collisional processes that can efficiently remove it from the gas.
When the fractional ionization of the gas is low, the rate at which H2 forms is limited primarily by the rate at which H- ions form via reaction 12, as any ions that form are rapidly converted to H2 by associative detachment with atomic hydrogen (reaction 13). If the fractional ionization is large, on the other hand, then many of the H- ions formed by reaction 12 do not survive for long enough to form H2, but instead are destroyed by mutual neutralization with H+ ions:
 |
(19) |
The ratio of the rates of reactions 13 and 19 is given by
k13 nH /
k19 nH+, where
nH is the number density of atomic hydrogen,
nH+ is the number
density of protons, and k13 and k19
are the rate coefficients for reactions 13 and 19, respectively. Mutual
neutralization therefore becomes significant whenever
nH+ / nH
 k13 /
k19. Although the value of k13 /
k19
is temperature dependent, the temperature dependence is weak if one uses
the best available determinations of the rate coefficients
(Kreckel et al. 2010
for reaction 13,
Stenrup, Larson
& Elander 2009
for reaction 19
1), and
k13 / k19 ~ 0.03 to within 50% for
all temperatures 100 < T < 104 K. If we compare
this value with the residual
fractional ionization of the intergalactic medium (IGM) at this epoch,
x ~ 2 × 10-4
(Schleicher et
al. 2008),
we see that mutual neutralization is unimportant within the very first
star-forming minihalos. It becomes important once larger minihalos, with
virial temperatures Tvir ~ 104 K or above,
begin to form, as in these minihalos, substantial collisional ionization
of the gas can occur, leading to an initial fractional ionization much
higher than the residual value in the IGM. It also becomes an important
process within the "fossil" HII regions left behind by the fossil HII
region first generation of massive stars
(Oh & Haiman 2003,
Nagakura & Omukai
2005,
Glover, Savin &
Jappsen 2006,
Kreckel et al. 2010).
k13 /
k19. Although the value of k13 /
k19
is temperature dependent, the temperature dependence is weak if one uses
the best available determinations of the rate coefficients
(Kreckel et al. 2010
for reaction 13,
Stenrup, Larson
& Elander 2009
for reaction 19
1), and
k13 / k19 ~ 0.03 to within 50% for
all temperatures 100 < T < 104 K. If we compare
this value with the residual
fractional ionization of the intergalactic medium (IGM) at this epoch,
x ~ 2 × 10-4
(Schleicher et
al. 2008),
we see that mutual neutralization is unimportant within the very first
star-forming minihalos. It becomes important once larger minihalos, with
virial temperatures Tvir ~ 104 K or above,
begin to form, as in these minihalos, substantial collisional ionization
of the gas can occur, leading to an initial fractional ionization much
higher than the residual value in the IGM. It also becomes an important
process within the "fossil" HII regions left behind by the fossil HII
region first generation of massive stars
(Oh & Haiman 2003,
Nagakura & Omukai
2005,
Glover, Savin &
Jappsen 2006,
Kreckel et al. 2010).
Although H2 is by far the most abundant primordial molecule,
it is actually not a particularly efficient coolant. The H2
molecule has no dipole moment, and so dipole transitions between its
excited rotational and vibrational levels are forbidden. Although
radiative transitions between levels do occur, they are quadrupole
transitions and the associated transition rates are small. In addition,
application of the Pauli exclusion principle to the hydrogen molecule
shows that it must have two distinct states, distinguished by the
nuclear spin of the two hydrogen nuclei: para-hydrogen, in which the
nuclear spins are parallel, and which must have an even value for the
rotational quantum number J, and ortho-hydrogen, which has
anti-parallel nuclear spins and an odd value for J. Radiative
transitions between ortho-hydrogen and para-hydrogen involve a change in
orientation of the spin of one of the nuclei and are therefore strongly
forbidden. As a result, the least energetic rotational transition of
H2 that has any significant probability of occurring is the
transition between the J = 2 and J = 0 rotational levels
in the vibrational ground-state of para-hydrogen. This transition has an
associated energy E20 / k
 512 K. The
H2 molecule therefore has large energy separations between
the ground state and any of the accessible excited rotational or
vibrational states
2, and
has only weak radiative transitions between these states.
512 K. The
H2 molecule therefore has large energy separations between
the ground state and any of the accessible excited rotational or
vibrational states
2, and
has only weak radiative transitions between these states.
These features of the H2 molecule have two important consequences. First, it becomes a very inefficient coolant at temperatures T ≪ E20 / K, as it becomes almost impossible to collisionally populate any of the excited states. The minimum temperature that can be reached solely with H2 cooling depends somewhat on the H2 abundance and the time available for cooling, but typically Tmin ~ 150-200 K. Second, its rotational and vibrational levels reach their local thermodynamic equilibrium (LTE) level populations at a relatively low density, ncrit ~ 104 cm-3. This means that at densities n ≫ ncrit, the H2 cooling rate scales only linearly with density and the cooling time due to H2 becomes independent cooling time of density. Since other important timescales, such as the free-fall collapse time of the gas, continue to decrease with increasing density, the implication is that H2 becomes an increasingly ineffective coolant as one moves to higher densities. molecular hydrogen!cooling|)
For these reasons, primordial molecules or molecular ions that do not share these drawbacks have attracted a certain amount of attention. In an early study, Lepp & Shull (1984) suggested that deuterated hydrogen, HD, and lithium hydride, LiH, may both be significant coolants in primordial gas. More recently, work by Yoshida et al. (2007) has suggested that H2+ may be an important coolant in some circumstances, while Glover & Savin (2006) show that H3+ is also worthy of attention. In practice, the only one of these molecules or ions that has proved to be important is HD. Detailed modelling of the chemistry of lithium in primordial gas (e.g. Stancil, Lepp & Dalgarno 1996, Mizusawa, Omukai & Nishi 2005) has shown that LiH is efficiently destroyed by the reaction
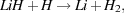 |
(20) |
and that only a small fraction of the available lithium (which itself has an abundance of only 5 × 10-10 relative to hydrogen; see Cyburt, Fields & Olive 2008) is ever incorporated into LiH. Cooling from the molecular ion H2+ was re-examined by Glover & Savin (2009), who showed that the collisional excitation rates cited by Galli & Palla (1998) and used as a basis for the fits given in Yoshida et al. (2007) were a factor of ten too large, and that if the correct rates are used, H2+ cooling is no longer important. Finally, Glover & Savin (2009) also examined the possible role played by H3+ cooling in considerable detail, but found that even if one makes optimistic assumptions regarding its formation rate and collisional excitation rate, it still contributes to the total cooling rate at the level of only a few percent, and hence at best is a minor correction term.
These studies leave HD as the only viable alternative to H2 as a coolant of primordial gas. HD has a small, but non-zero dipole moment, giving it radiative transition rates that are somewhat larger than those of H2, resulting in a critical density ncrit ~ 106 cm-3. Unlike H2, it is not separated into ortho and para states, and so the lowest energy transition accessible from the ground state is the J = 1 to J = 0 rotational transition, with an energy E10 / k = 128 K. Although the cosmological ratio of deuterium to hydrogen is small [D/H = (2.49 ± 0.17) × 10-5; Cyburt, Fields & Olive 2008], the ratio of HD to H2 can be significantly boosted in low temperature gas by chemical fractionation. The reaction
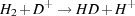 |
(21) |
that converts H2 into HD is exothermic and so proceeds rapidly at all temperatures, while the inverse reaction
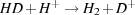 |
(22) |
is endothermic and so proceeds very slowly at low temperatures. In equilibrium, these two reactions produce an HD-to-H2 ratio given by
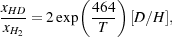 |
(23) |
where [D/H] is the cosmological D:H ratio. Together, these factors render HD a much more effective coolant than H2 in low temperature gas.
In practice, for HD cooling to take over from H2 cooling, the gas must already be fairly cold, with T ~ 150 K (Glover 2008), and temperatures this low are typically not reached during the collapse of the first star-forming minihalos, meaning that HD remains a minor coolant (Bromm, Coppi & Larson 2002). However, there are a number of situations, typically involving gas with an enhanced fractional ionization, in which HD cooling does become significant (see e.g. Nakamura & Umemura 2002, Nagakura & Omukai 2005, Johnson & Bromm 2006, Yoshida et al. 2007, McGreer & Bryan 2008, Greif et al. 2008, Kreckel et al. 2010).
1.3. The minimum mass scale for collapse
The relative simplicity of the chemistry discussed in the previous section allows one to construct a very simple model that captures the main features of the evolution of the H2 fraction within low density gas falling into a dark matter minihalo. We start by assuming that radiative recombination is the only process affecting the electron abundance, and writing the rate of change of the electron number density as
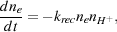 |
(24) |
where ne is the number density of electrons, nH+ is the number density of protons, and krec is the recombination coefficient. If we assume that ionized hydrogen is the only source of free electrons, implying that ne = nH+, and that the temperature remains roughly constant during the evolution of the gas, then we can solve for the time evolution of the electron fraction:
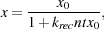 |
(25) |
where x  ne / n, n is the number density of
hydrogen nuclei, and
x0 is the initial value of x. We next assume
that all of the H2 forms via
the H- pathway, and that mutual neutralization of
H- with H+ (reaction 19) is the
only process competing with associative detachment (reaction 13) for the
H- ions. In this case, we can write the time evolution of the
H2 fraction, xH2
ne / n, n is the number density of
hydrogen nuclei, and
x0 is the initial value of x. We next assume
that all of the H2 forms via
the H- pathway, and that mutual neutralization of
H- with H+ (reaction 19) is the
only process competing with associative detachment (reaction 13) for the
H- ions. In this case, we can write the time evolution of the
H2 fraction, xH2
 nH2 / n, as
nH2 / n, as
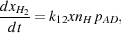 |
(26) |
where k12 is the rate coefficient of reaction 12, the formation of H- by the radiative association of H and e-, and pAD is the probability that any given H- ion will be destroyed by associative detachment rather than by mutual neutralization. Given our assumptions above, this can be written as
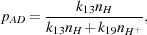 |
(27) |
where k13 is the rate coefficient for reaction 13 and
k19 is the rate coefficient for reaction 19. If we
again assume that ne =
nH+, and in addition assume that
nH
 n, then
the expression for pAD can be simplified to
n, then
the expression for pAD can be simplified to
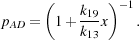 |
(28) |
Substituting this into Equation 26, we obtain
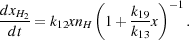 |
(29) |
If the initial fractional ionization x0 ≪ k13 / k19, then the term in parentheses is of order unity and this equation has the approximate solution
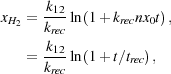 |
(30) (31) |
where trec = 1 / (krec n x0) is the recombination time. The growth of the H2 fraction is therefore logarithmic in time, with most of the H2 forming within the first few recombination times. In the more complicated case in which x0 is comparable to or larger than k13 / k19, but still significantly less than unity (so that nH ~ n), the H2 fraction is given instead by
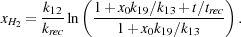 |
(32) |
From this analysis, we see that the main factor determining the final H2 abundance is the ratio k12 / krec, since for times of the order of a few recombination times, the logarithmic term in Equation 32 is of order unity, implying that the final H2 abundance is at most a factor of a few times k12 / krec. If we use the simple power-law fits to k12 and krec given by Hutchins (1976), namely k12 = 1.83 × 10-18 T0.8779 cm3 s-1 and krec = 1.88 × 10-10 T-0.644 cm3 s-1, then we can write the ratio of the two rate coefficients as
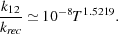 |
(33) |
The amount of H2 produced is a strong function of temperature, but is of the order of a few times 10-3 for temperatures of a few thousand Kelvin. We see therefore that the formation of H2 via H- never results in a gas dominated by H2, as the H2 abundance always remains much smaller than the abundance of atomic hydrogen.
Given this simple model for the amount of H2 that will form in the gas, the obvious next step is to compare this to the amount of H2 that is required to cool the gas efficiently. In order to determine the H2 fraction necessary to significantly cool gas with a temperature T within some specified fraction of the Hubble time - say 20% of tH - we can simply equate the two timescales, and solve for the H2 fraction. Using our previous definition of the cooling time, we have cooling time
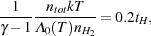 |
(34) |
where we have assumed that H2 is the dominant coolant and
have written the cooling rate per unit volume in terms of
 0, the
cooling rate per H2
molecule. Rearranging this equation, using the fact that when the
H2 fraction and the ionization level are low,
0, the
cooling rate per H2
molecule. Rearranging this equation, using the fact that when the
H2 fraction and the ionization level are low,
 = 5/3
and ntot = (1 + 4 xHe)
n, where xHe is the fractional
abundance of helium (given by xHe = 0.083 for
primordial gas), we obtain
= 5/3
and ntot = (1 + 4 xHe)
n, where xHe is the fractional
abundance of helium (given by xHe = 0.083 for
primordial gas), we obtain
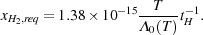 |
(35) |
In the high-redshift limit where tH
 H0-1
H0-1
 m-1/2 (1 + z)-3/2,
this becomes
m-1/2 (1 + z)-3/2,
this becomes
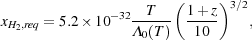 |
(36) |
where we have used values for the cosmological parameters taken from
Komatsu et al. (2011).
Collisions of H2 with a number of different species
contribute to
 0, as
explored in
Glover & Abel
(2008),
but in the earliest minihalos, the dominant contributions come from
collisions with H and He.
0, as
explored in
Glover & Abel
(2008),
but in the earliest minihalos, the dominant contributions come from
collisions with H and He.
 0 is
therefore given to a good approximation by
0 is
therefore given to a good approximation by
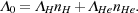 |
(37) |
Simple fits for the values of
 H and
H and
 He as a
function of temperature can be found in
Glover & Abel
(2008).
He as a
function of temperature can be found in
Glover & Abel
(2008).
An illustration of the likely size of xH2,
req is given in
Figure 2. In this Figure, we plot
xH2, req as a function of
temperature, evaluated for three different redshifts: z = 20, 30
and 40. In computing these values, we have assumed
that the mean density of the gas in the minihalo is given by
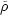 =
=
 c
c
 b,0,
where
b,0,
where
 0
is the cosmological background density of baryons. In
the Figure, we also show the actual H2
fraction produced in the gas,
xH2, act, as a function of temperature at
times equal to 1, 5
and 10 recombination times, and where we have taken
x0 ≪ k13 / k19.
0
is the cosmological background density of baryons. In
the Figure, we also show the actual H2
fraction produced in the gas,
xH2, act, as a function of temperature at
times equal to 1, 5
and 10 recombination times, and where we have taken
x0 ≪ k13 / k19.
Figure 2 demonstrates that the amount of H2 produced in the gas is a strongly increasing function of temperature, while the amount required to bring about efficient cooling of the gas is a strongly decreasing function of temperature. This means that for any given choice of comparison time t and redshift z, we can identify a critical temperature Tcrit, such that gas with T > Tcrit will cool within a small fraction of a Hubble time, while gas with T < Tcrit will not. Moreover, because xH2, act and xH2, req are both steep functions of temperature, but are relatively insensitive to changes in t or z, the value of Tcrit that we obtain is also relatively insensitive to our choices for t or z. We find that Tcrit ~ 1000 K, and that at this temperature, the H2 fraction required to provide efficient cooling lies somewhere between a few times 10-4 and 10-3 (c.f. Tegmark et al. 1997 who come to a similar conclusion using a very similar argument). If we convert this critical virial temperature into a corresponding critical minihalo mass using Equation 10, we find that
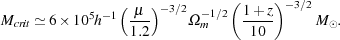 |
(38) |
This mass scale is illustrated by the dotted line in
Figure 1. At high redshift, it is smaller than the
filter mass scale corresponding to vbc =
 vbc,
demonstrating that at these redshifts, it
is the streaming of the gas with respect to the dark matter that is the
main process limiting the formation of
Population III stars. Below a redshift of around 40, however,
Mcrit becomes the larger mass scale,
implying that at these lower redshifts, there will be a population of
small minihalos that contain a significant
gas fraction, but that do not form stars, because their gas is unable to
cool in less than a Hubble time.
These small starless minihalos may be important sinks for ionizing
photons during the epoch of reionization
(Haiman, Abel &
Madau 2001).
vbc,
demonstrating that at these redshifts, it
is the streaming of the gas with respect to the dark matter that is the
main process limiting the formation of
Population III stars. Below a redshift of around 40, however,
Mcrit becomes the larger mass scale,
implying that at these lower redshifts, there will be a population of
small minihalos that contain a significant
gas fraction, but that do not form stars, because their gas is unable to
cool in less than a Hubble time.
These small starless minihalos may be important sinks for ionizing
photons during the epoch of reionization
(Haiman, Abel &
Madau 2001).
To conclude our discussion of the first star-forming minihalos, we should mention one potentially important effect not taken into account in the analysis above. This is the influence of ongoing minor mergers and accretion on the thermal balance of the gas. Although major mergers occur only once per Hubble time, on average, minor mergers occur far more frequently, and act to stir up the gas, thereby heating it and lengthening the time required for it to cool. This phenomenon was noted by Yoshida et al. (2003) in their cosmological simulations of the formation of the first star-forming minihalos. Yoshida et al. (2003) show that in spite of the approximations made in its derivation, Equation 38 gives a reasonable guide to the minimum mass of the minihalos that contain gas that can cool effectively. However, they also find that there are some minihalos with M > Mcrit in which the gas does not cool. They show that these minihalos have higher mass accretion rates than minihalos of the same mass in which cooling does occur, and hence ascribe the suppression of cooling to the effects of dynamical heating by the ongoing accretion and minor mergers. This effect was also treated more recently by Wang & Abel (2008), who show that it can be included into the simple thermal model described above by the addition of a heating term describing the effects of mergers and accretion. They show that if one writes this heating term as
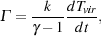 |
(39) |
then one can relate the rate of change of the virial temperature to the mass growth rate of the minihalo in a relatively simple fashion.
1 A group lead by X. Urbain at the Université Catholique de Louvain has recently made new experimental measurements of the rate of this reaction at low temperatures, but at the time of writing, the results of this work remain unpublished Back.
2 For comparison, note that the energy separation between the J = 0 and J = 1 rotational levels of CO is roughly 5 K. Back.