2. GRAVITATIONAL COLLAPSE AND THE FORMATION OF THE FIRST PROTOSTAR

As the analysis in the previous section has shown, gas in minihalos with virial temperatures greater than about 1000 K (corresponding to masses M ~ 10⁶ M) can form enough H₂ to cool within a small fraction of a Hubble time. This reduces the pressure and allows the gas to collapse further under the influence of its own self-gravity. As it does so, the value of the Jeans mass decreases. Many early studies of the formation of primordial stars assumed that as the Jeans mass decreases and the gas becomes more gravitationally unstable, it begins to undergo hierarchical gravitational fragmentation in a manner similar to that envisaged by Hoyle (1953), with the result that at any given moment, the mean fragment mass is approximately equal to the local Jeans mass (see Glover 2005 for a historical summary of these models). In this picture, one could predict the final mass of the first stars simply by studying the evolution of the Jeans mass. Moreover, since the minimum Jeans reached during the collapse can be estimated with reasonable accuracy on purely thermodynamical grounds (Rees 1976, Low & Lynden-Bell 1976), in this view of Population III star formation, the dynamics of the gas is of secondary importance. Around ten years ago, however, it first became possible to model the coupled chemical, dynamical and thermal evolution of the gas within a primordial minihalo using high resolution 3D numerical simulations (Abel, Bryan & Norman 2000, Abel, Bryan & Norman 2002, Bromm, Coppi & Larson 1999, Bromm, Coppi & Larson 2002). These studies showed that the picture outlined above is wrong: the gas does not undergo hierarchical fragmentation, and so one cannot predict the masses of the first stars simply by studying the evolution of the Jeans mass. These high resolution numerical simulations, and the many that have followed Jeans mass them (e.g. Yoshida et al. 2006, O'Shea & Norman 2007, McGreer & Bryan 2008) to name but a few), have for the first time given us a clear picture of exactly how gravitational collapse proceeds within one of these early minihalos. In the next section, we will discuss the sequence of events that occur as we follow the collapse from the minihalo scale all the way down to the scale of a single Population III protostar. Following that, in Sections 2.2 and 2.3 we discuss two of the main uncertainties remaining in our model for the formation of the first Pop. III protostar: the role played by heating and ionization arising from dark matter self-annihilation (Section 2.2) and the role played by magnetic fields (Section 2.3).

2.1. Thermal and chemical evolution of the gas during collapse

2.1.1. Initial collapse

As gas falls into the minihalo from the intergalactic medium, it is shock-heated to a temperature close to T_vir. In the post-shock gas, the electron fraction decreases due to radiative recombination, but at the same time H₂ forms, primarily via reactions 12 and 13. As we have already seen, the H₂ fraction evolves logarithmically with time, with most of the H₂ forming within the first few recombination times. As the H₂ fraction increases, so does its ability to cool the gas, and so the gas temperature slowly decreases, reducing the pressure and allowing the gas to collapse to the centre of the minihalo.

At this point, the evolution of the gas depends upon how much H₂ it has formed. There are two main outcomes, and which one occurs within a given minihalo depends primarily on the initial ionization state of the gas.

The low ionization case

During the formation of the very first Population III stars (also known as Population III.1, to use the terminology introduced by Tan & McKee 2008), the initial fractional ionization of the gas is the same as the residual ionization in the intergalactic medium, i.e. x₀ ~ 2 × 10^-4. In this case, the amount of H₂ that forms in the gas is typically enough to cool it to a temperature of T ~ 200 K but not below. At this temperature, chemical fractionation has already increased the HD/H₂ ratio by a factor of 20 compared to the cosmic deuterium-to-hydrogen ratio, and as a consequence, HD is starting to become an important coolant. However, the amount of HD that forms in the gas is not enough to cool it significantly below 200 K (Bromm, Coppi & Larson 2002), and H₂ continues to dominate the cooling and control the further evolution of the gas. In this scenario, the collapse of the gas is greatly slowed once its temperature reaches 200 K and its density reaches a value of around 10⁴ cm^-3, corresponding to the critical density n_crit, at which the rotational and vibrational level populations of H₂ approach their local thermodynamic equilibrium (LTE) values. At densities higher than this critical density, the H₂ cooling rate per unit volume scales only linearly with n (compared to a quadratic dependence, _H2 n² at lower densities), while processes such as compressional heating continue to increase more rapidly with n. As a result, the gas temperature begins to increase once the density exceeds n_crit.

Gas reaching this point in the collapse enters what Bromm, Coppi & Larson (2002) term a "loitering" phase, during which cold gas accumulates in the centre of the halo but only slowly increases its density. This loitering phase ends once the mass of cold gas that has accumulated exceeds the local value of the Bonnor-Ebert mass (Bonnor 1956, Ebert 1955), given in this case by Abel, Bryan & Norman (2002)

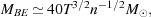(40)

which for n ~ 10⁴ cm^-3 and T ~ 200 K yields M_BE ~ 1000 M. ³ Once the mass of cold gas exceeds M_BE, its collapse speeds up again, and becomes largely decoupled from the larger-scale behaviour of the gas. The next notable event to occur in the gas is the onset of three-body H₂ formation, which is discussed in the next section.

The high ionization case

If the initial fractional ionization of the gas is significantly higher than the residual fraction in the IGM, then a slightly different chain of events can occur. A larger initial fractional ionization implies a shorter recombination time, and hence a logarithmic increase in the amount of H₂ formed after a given physical time. An increase in the H₂ fraction allows the gas to cool to a slightly lower temperature, and hence boosts the HD abundance in two ways: the lower temperature increases the HD/H₂ ratio produced by fractionation, and the H₂ fraction itself is larger, so any given HD/H₂ ratio corresponds to a higher HD abundance than in the low ionization case. If the addition ionization allows enough H₂ to be produced to cool the gas to T ~ 150 K (which requires roughly a factor of three more H₂ than is required to reach 200 K), then chemical fractionation increases the HD abundance to such an extent that it takes over as the dominant coolant (Glover 2008). This allows the gas to cool further, in some cases reaching a temperature as low as the CMB temperature, T_CMB (e.g. Nakamura & Umemura 2002, Nagakura & Omukai 2005, Johnson & Bromm 2006, Yoshida et al. 2007, McGreer & Bryan 2008, Kreckel et al. 2010). The higher critical density of HD, n_{crit, HD} ~ 10⁶ cm^-3, means that the gas does not reach the loitering phase until much later in its collapse. Once the gas does reach this phase, however, its subsequent evolution is very similar to that in the low-ionization case discussed above. Cold gas accumulates at n ~ n_crit until its mass exceeds the Bonnor-Ebert mass, which in this case is M_BE ~ 40 M if T = 100 K and n = 10⁶ cm^-3. Once the gas mass exceeds M_BE, the collapse speeds up again, and the gas begins to heat up. Aside from the substantial difference in the size of M_BE, the main difference between the evolution of the gas in this case and in the low ionization case lies in the fact that in the high ionization case, the gas reheats from T ~ 200 K or below to T ~ 1000 K much more rapidly than in the low ionization case. As we shall see later, this period of rapid heating has a profound influence on the ability of the gas to fragment.

Several different scenarios have been identified that lead to an enhanced fractional ionization in the gas, and that potentially allow the gas to reach the HD-dominated regime. Gas within minihalos with T_vir > 9000 K will become hot enough for collisional ionization of hydrogen to supply the necessary electrons. However, as halos of this size will typically have at least one star-forming progenitor (Johnson, Greif & Bromm 2008), it is questionable whether many Pop. III stars will form in such minihalos, as we would expect the gas in most of them to have been enriched with metals by one or more previous episodes of star formation.

Another possibility that has attracted significant attention involves the gas in the minihalo being drawn from a "fossil" HII region, i.e. a region that was formerly ionized by a previous Population III protostar fossil HII region but has now recombined (see e.g. Oh & Haiman 2003, Nagakura & Omukai 2005, Yoshida et al. 2007). Many studies have shown that the volume of the IGM ionized by a single massive Pop. III star is significantly larger than the volume that is enriched by the metals produced in the supernova occurring at the end of the massive star's life (see e.g. the recent treatment by Greif et al. (2010), or Ciardi & Ferrara (2005) for a summary of earlier work). It is therefore possible that a significant number of Population III stars may form in such conditions.

A final possibility is that the required ionization can be produced by a flux of X-rays or high energy cosmic rays. Although X-ray ionization was initially favoured as a means of raising the ionization level of the gas, and hence promoting H₂ formation (Haiman, Abel & Rees 2000), more recent work has shown that if one considers realistic models for the X-ray background that also account for the simultaneous growth of the soft UV background, then one finds that UV photodissociation of the H₂ is a more important effect, and hence that the growth of the radiation photodissociation backgrounds almost always leads to an overall reduction in the amount of H₂ produced (Glover & Brand 2003, Machacek, Bryan & Abel 2003). Cosmic ray ionization may therefore prove to be the more important effect (Stacy & Bromm 2007, Jasche, Ciardi & Ensslin 2007), although we still know very little about the likely size of the cosmic ray ionization rate in high redshift minihalos.

2.1.2. Three-body H₂ formation

Once the collapsing gas reaches a density of around 10⁸-10⁹ cm^-3, its chemical makeup starts to change significantly. The reason for this is that at these densities, the formation of H₂ via the three-body reactions (Palla, Salpeter, & Stahler 1983)

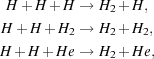(41) (42) (43)

starts to become significant. These reactions quickly convert most of the hydrogen in the gas into H₂. At the same time, however, they generate a substantial amount of thermal energy: every time an H₂ molecule forms via one of these three-body reactions, its binding energy of 4.48 eV is converted into heat. A simple estimate of the relative sizes of the compressional heating rate and the three-body H₂ formation heating rate helps to demonstrate the importance of the latter during this stage of the collapse. Let us consider gas at a density n = 10⁸ cm^-3 that has a temperature T = 1000 K, collapsing at a rate such that dn / dt = n / t_ff, where t_ff is the gravitational free-fall time. In these conditions, the compressional heating rate is given by

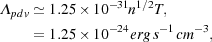(44) (45)

while the three-body H₂ formation heating rate has the value

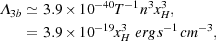(46) (47)

where we have adopted the rate coefficient for reaction41 given in Palla, Salpeter, & Stahler (1983). Comparing the two heating rates, we see that three-body H₂ formation heating dominates unless x_H is very small (i.e. unless the gas is almost fully molecular). Therefore, even though the abundance of H₂, the dominant coolant during this phase of the collapse, increases by more than two orders of magnitude, the gas typically does not cool significantly, owing to the influence of this three-body H₂ formation heating. Indeed, the temperature often actually increases.

One major uncertainty that remains in current treatments of this phase of the collapse of the gas is exactly how quickly the gas becomes molecular. Although reaction 41 is the dominant source of H₂ at these densities, the rate coefficient for this reaction is poorly known, with published values differing by almost two orders of magnitude at 1000 K, and by an even larger factor at lower temperatures (Glover 2008, Turk et al. 2011). The effects of this uncertainty have recently been studied by Turk et al. (2011). They show that it has little effect on the density profile of the gas, and only a limited effect on the temperature profile. However, it has much more significant effects on the morphology of the gas and on its velocity structure. Simulations in which a high value was used for the three-body rate coefficient show find that gas occurs more rapidly, and that the molecular gas develops a much more flattened, filamentary structure. Significant differences are also apparent in the infall velocities and the degree of rotational support. Turk et al. (2011) halt their simulations at the point at which a protostar first forms, and so do not directly address the issue of whether these differences continue to have an influence during the accretion phase, and whether the affect the ability of the gas to fragment (see Section 3.2 below). A follow-up study that focussed on these issues would be informative.

2.1.3. Optically-thick line cooling

The next important event occurs at a density of around 10¹⁰ cm^-3, when the main rotational and vibrational lines of H₂ start to become optically thick (Ripamonti & Abel 2004). The effect of this is to reduce the efficiency of H₂ cooling, leading to a continued rise in the gas temperature. In one-dimensional simulations (e.g. Omukai & Nishi 1998, Omukai et al. 1998, Ripamonti et al. 2002), it is possible to treat optically thick H₂ cooling accurately by solving the full radiative transfer problem. These models show that although the optical depth of the gas becomes large at frequencies corresponding to the centers of the main H₂ emission lines, the low continuum opacity of the gas allows photons to continue to escape through the wings of the lines, with the result that the H₂ cooling rate is suppressed far less rapidly as the collapse proceeds than one might at first expect (see Omukai et al. 1998 for a detailed discussion of this point).

In three-dimensional simulations, solution of the full radiative transfer problem is not currently possible, due to the high computational expense, which has motivated a search for simpler approximations. There are two such approximations in current use in simulations of Population III star formation. The first of these was introduced by Ripamonti & Abel (2004). They proposed that the ratio of the optically thick and optically thin H₂ cooling rates,

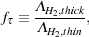(48)

could be represented as a simple function of density:

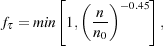(49)

where n₀ = 8 × 10⁹ cm^-3. They showed that this simple expression was a good approximation to the results of the full radiative transfer model used by Ripamonti et al. (2002), and suggested that this approximation would be useful for extending the results of three-dimensional simulations into the optically thick regime. However, they also noted that it may only be accurate while the collapse remains approximately spherical, as the one-dimensional model on which it is based assumes spherical infall.

An alternative approach was introduced by Yoshida et al. (2006). They compute escape probabilities for each rotational and vibrational line of H₂ using the standard Sobolev Sobolev approximation (Sobolev 1960). In this approximation, the optical depth at line centre of a transition from an upper level u to a lower level l is written as

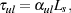(50)

where _ul is the line absorption coefficient and L_s is the Sobolev length. The absorption coefficient _ul can be written as

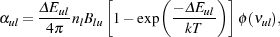(51)

where E_ul is the energy difference between the two levels, n_l is the number density of H₂ molecules in the lower levels, B_lu is the usual Einstein B coefficient, and (_ul) is the line profile at the centre of the line. The Sobolev length is given by

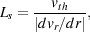(52)

where v_th is the thermal velocity of the H₂ and |dv_r / dr | is the size of the velocity gradient along a given line of sight from the fluid element of interest. Given _ul, the escape probability for photons emitted in that direction then follows as

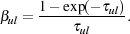(53)

To account for the fact that the velocity gradient may differ along different lines of sight from any particular fluid element, Yoshida et al. (2006) utilize a mean escape probability given by

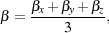(54)

where _x, _y and _z are the escape probabilities along lines of sight in the x, y and z directions, respectively. Finally, once the escape probabilities for each transition have been calculated, the optically thick H₂ cooling rate can be computed from

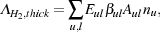(55)

where A_ul is the Einstein A coefficient for the transition from u to l and n_u is the population of the upper level u.

Strictly speaking, the Sobolev approximation is valid only for flows in which the Sobolev length L_s is much smaller than the characteristic length scales associated with changes in the density, temperature or chemical makeup of the gas, a requirement which is easy to satisfy when the velocity gradient is very large, but which is harder to justify in the case of Population III star formation, since the collapse speed is typically comparable to the sound-speed. Nevertheless, Yoshida et al. (2006) show that the optically thick H₂ cooling rates predicted by the Sobolev approximation are in very good agreement with those computed in the one-dimensional study of Omukai & Nishi (1998) by solution of the full radiative transfer problem.

Little work has been done on comparing these two approaches to treating optically-thick H₂ cooling. This issue was addressed briefly in Turk et al. (2011), who showed that the two approximations yielded similar values for f for densities n < 10¹⁵ cm^-3 during the initial collapse of the gas, with differences of at most a factor of two. However, as yet no study has examined whether this good agreement persists past the point at which the first protostar forms.

2.1.4. Collision-induced emission

A further significant point in the collapse of the gas is reached once the number density increases to n ~ 10¹⁴ cm^-3. At this density, a process known as collision-induced emission becomes important. Although an isolated H₂ molecule has no dipole moment, and can only emit or absorb radiation through quadrupole transitions, when two H₂ molecules collide ⁴ they briefly act as a kind of "supermolecule" with a non-zero dipole moment for the duration of the collision. This supermolecule can therefore absorb or emit radiation through dipole transitions, which have much higher transition probabilities than the quadrupole transitions available to isolated H₂. If radiation is absorbed, this process is termed collision-induced absorption; if it is emitted, then we refer to the process as collision-induced emission (CIE). A detailed discussion of the phenomenon can be found in Frommhold (1993).

Collision-induced emission can in principle occur in gas of any density, but the probability of a photon being emitted in any given collision is very small, owing to the short lifetime of the collision state ( t < 10^-12 s at the temperatures relevant for Pop. III star formation; see Ripamonti & Abel 2004). For this reason, CIE becomes an important process only at very high gas densities. Another consequence of the short lifetime of the collision state is that the individual lines associated with the dipole transitions become so broadened that they actually merge into a continuum. This is important, as it means that the high opacity of the gas in the rovibrational lines of H₂ does not significantly reduce the amount of energy that can be radiated away by CIE. Therefore, once the gas reaches a sufficiently high density, CIE becomes the dominant form of cooling, as pointed out by several authors (Omukai & Nishi 1998, Ripamonti et al. 2002, Ripamonti & Abel 2004).

The most detailed study of the effects of CIE cooling on the collapse of primordial gas was carried out by Ripamonti & Abel (2004). They showed that CIE cooling could actually become strong enough to trigger a thermal instability, However, the growth rate of this instability is longer than the gravitational free-fall time, meaning that it is unlikely that this process can drive fragmentation during the initial collapse of the gas.

2.1.5. Cooling due to H₂ dissociation

The phase of the collapse dominated by CIE cooling lasts for only a relatively short period of time. The gas becomes optically thick in the continuum once it reaches a density n ~ 10¹⁶ cm^-3 (Omukai & Nishi 1998, Ripamonti & Abel 2004), which strongly suppresses any further radiative cooling. Once this occurs, the gas temperature rises until it reaches a point at which the H₂ begins to dissociate. At these densities, this occurs at a temperature T ~ 3000 K. Once this point is reached, the temperature rise slows, as most of the energy released during the collapse goes into dissociating the H₂ rather than raising the temperature. As it takes 4.48 eV of energy to destroy each H₂ molecule, this H₂ dissociation phase continues for a while. However, it comes to an end once almost all of the H₂ has been destroyed, at which point the temperature of the gas begins to climb steeply. The thermal pressure in the interior of the collapsing core rises rapidly and eventually becomes strong enough to halt the collapse. At the point at which this occurs, the size of the dense core is around 0.1 AU, its mass is around 0.01 M and its mean density is of order 10²⁰ cm^-3 (Yoshida, Omukai & Hernquist 2008). It is bounded by a strong accretion shock. This pressure-supported, shock-bounded core is a Population III protostar, and its later evolution is discussed in Section 3 below.

2.2. Dark matter annihilation

One complication not accounted for in the models of Pop. III star formation described above is the role that may be played by dark matter annihilation. The nature of dark matter is not yet understood, but one plausible candidate is a weakly interacting massive particle (WIMP) - specifically, the lightest WIMP supersymmetric particle predicted in models based on supersymmetry. The simplest supersymmetry models predict that this WIMP has an annihilation cross-section < v > ~ 3 × 10^-26 cm², a mass within the range of 50 GeV to 2 TeV, and a cosmological density consistent with the inferred density of dark matter (Spolyar et al. 2008). The rate per unit volume at which energy is produced by dark matter annihilation can be written as Q_ann = < v > _x² / m_x, where _x is the mass density of dark matter and m_x is the mass of a single dark matter particle. For a plausible particle mass of 100 GeV, and a dark matter density equal to the cosmological background density of dark matter, this expression yields a tiny heating rate, Q_ann ~ 6 × 10^-62 (1 + z)⁶ _m² h⁴ erg cm^-3 s^-1, even before one accounts for the fact that much of the annihilation energy is released in the form of energetic neutrinos or gamma-rays that couple only very weakly with the intergalactic gas. WIMP annihilation therefore plays no significant role in the evolution WIMP of the intergalactic medium while the WIMPs remain uniformly distributed (Myers & Nusser 2008). However, the _x² density dependence of the heating rate means that it can potentially become significant in regions where the dark matter density is very high.

Spolyar et al. (2008) proposed that one situation in which the heating from dark matter annihilation could become important would occur during the formation of the very first Population III protostars. They assumed that any given star-forming minihalo would form only a single Pop. III protostar, and that this protostar would form at the center of the minihalo. As the gas collapsed at the center of the minihalo, its increasing gravitational influence would bring about a local enhancement of the dark matter density, via a process known as adiabatic contraction. adiabatic contraction The basic idea underlying this is very simple. For a collisionless particle on a periodic orbit, the quantity 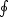p dq, where p is the conjugate momentum of coordinate q, is an adiabatic invariant, i.e. a quantity that does not vary when the gravitational potential varies, provided that the rate of change of the potential is sufficiently slow. If p represents the angular momentum of a particle on a circular orbit of radius r within some spherically symmetric mass distribution, then one can show that the quantity r M(r) is constant for that particle, where M(r) is the mass enclosed within r, so long as this enclosed mass changes on a timescale that is long compared to the orbital period. Spolyar et al. (2008) show that if one starts with a simple NFW profile for the dark matter (Navarro, Frenk & White 1997) and account for the effects of adiabatic contraction using a simple approach pioneered by Blumenthal et al. (1986), then one finds that for any WIMP mass less than 10 TeV, the effects of dark matter WIMP annihilation heating become significant during the collapse of the gas. Spolyar et al. (2008) identify the point at which this occurs by comparing the heating rate due to dark matter annihilation with the H₂ cooling rate. To determine a value for the latter, they make use of the simulation results of Yoshida et al. (2006) and Gao et al. (2007) and measure how the H₂ cooling rate of the gas in the central collapsing core evolves as the collapse proceeds. They show that for a 100 GeV WIMP, heating dominates at gas densities n > 10¹³ cm^-3. Finally, they argue that once dark matter annihilation heating dominates over H₂ cooling, the gravitational collapse of the gas will come to a halt, and hence the gas will never reach protostellar densities. Instead, it will remain quasi-statically supported at a density of roughly 10¹³ cm^-3 (for a 100 GeV WIMP), with WIMP a corresponding size scale of 17 AU, for as long as the dark matter annihilation rate remains large compared to the H₂ cooling rate. As the time required to consume all of the dark matter within a radius of 17 AU may be hundreds of millions of years, the resulting quasi-static gas distribution - dubbed a "dark star" dark star by Spolyar et al. (2008) - could potentially survive for a very long time.

One criticism of the original Spolyar et al. (2008) model is its reliance on the Blumenthal et al. (1986) prescription for describing the effects of the adiabatic contraction of the dark matter. adiabatic contraction This prescription assumes that all of the dark matter particles move on circular orbits, which is unlikely to be the case in a realistic dark matter minihalo, and concerns have been expressed that it may yield values for the dark matter density after adiabatic contraction that are significantly higher than the true values (see e.g. Gnedin et al. 2004). For this reason, Freese et al. (2009) re-examined this issue using an alternative method for estimating the effects of adiabatic contraction, based on Young (1980). This alternative prescription does account for particles moving on radial orbits, and Freese et al. (2009) show that it predicts dark matter densities that are indeed systematically smaller than those predicted by the Blumenthal et al. (1986) prescription, but only by a factor of two. Freese et al. (2009) therefore conclude that although using the Young (1980) prescription for adiabatic contraction in place of the simpler Blumenthal et al. (1986) prescription will lead to some minor quantitative changes in the predicted outcome, the main qualitative results of the Spolyar et al. (2008) study are insensitive to this change, and one would still expect a "dark star" to form.

Another potential problem with the dark star hypothesis is the fact that it is not at all clear that the collapse of the gas will stop once the dark matter heating rate exceeds the H₂ cooling rate. For one thing, the values for the H₂ cooling rate used by Spolyar et al. (2008) do not account for the effects of the dark matter annihilation heating. If this leads to an increase in temperature, then this will also increase the H₂ cooling rate, allowing more of the energy produced by dark matter annihilation to be radiated away. It is therefore unlikely that the point in the collapse at which the dark matter annihilation heating rate exceeds the Spolyar et al. estimate for the H₂ cooling rate is marked by any sharp jump in the temperature. Instead, we would expect to find a more gradual temperature increase, at least up until the point at which collisional dissociation of the H₂ starts to occur.

Once H₂ begins to dissociate, this provides another outlet for the energy generated by dark matter annihilation. Spolyar et al. estimate that for a 100 GeV WIMP, the power generated by dark matter WIMP annihilation within the central core is L_dm ~ 140 L, and the core mass is roughly 0.6 M. The total energy stored within the core in the form of the binding energy of the H₂ molecules is roughly

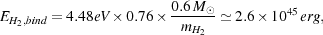(56)

and the time required for dark matter annihilation to produce this much energy is

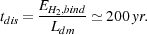(57)

For comparison, the free-fall time at this point in the collapse is roughly 15 years. H₂ dissociation will therefore allow the collapse of the gas to continue until either the dark matter heating rate becomes large enough to destroy the H₂ in the core in much less than a dynamical time, or the compressional heating produced during the collapse becomes capable of doing the same job. In either case, it is likely that much higher core densities can be reached than was assumed in the Spolyar et al. study.

A first attempt to hydrodynamically model the formation of a "dark star" while correctly accounting for dark star these thermodynamical effects was made by Ripamonti et al. (2010). They used the 1D, spherically symmetric hydrodynamical code described in Ripamonti et al. (2002) to model the collapse of the gas up to densities of order 10¹⁵ cm^-3 for a range of different WIMP masses between 1 GeV and 1 TeV. WIMP Adiabatic contraction of the dark matter was modelled using the algorithm described in Gnedin et al. (2004), and the effects of the dark matter annihilation heating and ionization were self-consistently accounted for in the chemical and thermal model. Ripamonti et al. (2010) show that even in the most extreme case that they study, the heating produced by the dark matter appears unable to halt the collapse for an extended period. After the dark matter heating rate exceeds the H₂ cooling rate, dissociation of H₂ in the core accounts for most of the "excess" energy not radiated away by the gas, allowing the collapse to continue. Once the H₂ in the core is exhausted, the temperature rises steeply, very briefly halting the collapse. However, the temperature quickly becomes large enough to allow other cooling mechanisms (e.g. H^- bound-free transitions or Lyman- emission from atomic hydrogen) to operate, allowing the collapse to restart. Ripamonti et al. (2010) do not find any evidence for the formation of a hydrostatically supported "dark star" up to the highest densities that they study. Confirmation of this result in a 3D treatment of the collapse would be very useful.

2.3. The role of magnetic fields

2.3.1. Initial strength

The majority of the work that has been done on modelling the formation of the first stars assumes that magnetic fields play no role in the process, either because no magnetic field exists at that epoch, or because the strength of any field that does exist is too small to be significant. A number of mechanisms have been suggested that may generate magnetic seed fields during the inflationary epoch, the electroweak phase transition or the QCD phase transition (see Kandus, Kunze & Tsagas 2011 for a recent comprehensive review). Observational constraints (e.g. Barrow, Ferreira & Silk 1997, Schleicher, Banerjee & Klessen 2008) limit the strength of the magnetic field at the epoch of first star formation to no more than about 1 nG (in comoving units), but it is quite possible that any primordial seed field resulting from one of these processes will actually have a much smaller strength.

An alternative source for magnetic fields within the first generation of star-forming minihalos is the so-called Biermann battery effect (Biermann 1950). In a partially ionized gas in which the gradient of electron density does not perfectly align with the gradient of electron pressure, as can happen if there is a temperature gradient that does not align with the pressure gradient, the magnetic induction equation takes the form

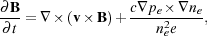(58)

where B is the magnetic field, v is the velocity, n_e is the electron density, p_e is the electron pressure, and e is the charge on an electron. In the limit that B 0, the first term on the right-hand side of this equation also becomes zero, but the battery term does not. It can therefore act as the source of a magnetic field in a gas that is initially unmagnetized. An early investigation into the effectiveness of the Biermann battery during galaxy formation was made by Kulsrud et al. (1997), who considered the formation of massive galaxies and showed that the Biermann battery could generate a field of strength B ~ 10^-21 G during their assembly. More recently, Xu et al. (2008) have simulated the action of the Biermann battery during the formation of one of the first star-forming minihalos, finding that it is able to generate initial field strengths of the order of 10^-18 G during this process.

2.3.2. Amplification

The seed fields generated by the Biermann battery, or by other processes acting in the very early Universe can be significantly amplified by flux-freezing during the gravitational collapse of the gas. If the diffusive timescale associated with ambipolar diffusion or Ohmic diffusion is long compared to the gravitational collapse timescale, then the magnetic field will be "frozen" to the gas, and will be carried along with it when the gas collapses.

In the optimal case of spherical collapse, perfect flux freezing implies that the field strength evolves with density as B ^2/3, and hence the magnetic pressure p_mag = B² / 8 evolves as p_mag ^4/3. In comparison, the thermal pressure p_therm evolves as p_therm T, and so if the temperature does not vary much during the collapse, the plasma parameter, p_therm / p_mag, evolves as ^-1/3. Therefore, if the gas is initially dominated by thermal pressure rather than magnetic pressure, it will remain so during much of the collapse, as a large change in the density is necessary to significantly alter . In the case examined by Xu et al. (2008), the very small initial magnetic field strength means that is initially very large, and remains so throughout the collapse, implying that the magnetic field never becomes dynamically significant. Moreover, even if we take an initial comoving field strength of 1 nG, comparable to the observational upper limit, at the mean halo density, ~ 10⁴ (assuming a halo formation redshift z = 20 and a virial temperature of 1000 K), and does not become of order unity until very late in the collapse. Furthermore, if the collapse of the gas is not spherical, whether because of the effects of gravitational forces, angular momentum, or the influence of the magnetic field itself, the amplification due to flux freezing and collapse will be less than in the spherical case (see e.g. Machida et al. 2006 who find a somewhat shallower relationship in some of their models).

Therefore, for magnetic fields to play an important role in Pop. III star formation, they must either start with a field strength very close to the observational upper limit, or we must invoke an amplification process that is much more effective than the amplification that occurs due to flux freezing and gravitational collapse. One obvious possibility is amplification via some kind of dynamo process, which could bring about exponential amplification of an initially small seed field. Of particular interest is the small-scale turbulent dynamo (Kraichnan & Nagarajan 1967, Kazantsev 1968, Kulsrud & Anderson 1992). This produces a magnetic field that has no mean flux on the largest scales but that can have substantial mean flux within smaller-scale subregions. The growth rate of the magnetic field due to the turbulent dynamo is closely related to the rate of turnover of the smallest eddies. If the magnetic field is sufficiently small that it does not significantly affect the velocity field of the gas (the kinematic approximation), and if we assume that we are dealing with Kolmogorov turbulence, then Kulsrud & Zweibel (2008) show that the magnetic energy density grows exponentially, and that after a single gravitational free-fall time it is amplified by a factor exp(Re^1/2), where Re is the Reynolds number of the flow. If we assume that the driving scale of the turbulence is comparable to the size of the minihalo, and that the turbulent velocity is of the same order as the sound speed (see e.g. Abel, Bryan & Norman 2002), then Re ~ 10⁴-10⁵, implying that the magnetic field is amplified by an enormous factor during the collapse. In practice, the field will not be amplified by as much as this analysis suggests, as the kinematic approximation will break down once the magnetic energy density becomes comparable to the kinetic energy density on the scale of the smallest eddies. Nevertheless, this simple treatment implies that the turbulent dynamo can amplify the magnetic field to a strength at which it becomes dynamically important.

Although the importance of dynamo processes during the formation of the first galaxies has been understood for a number of years (see e.g. Pudritz & Silk 1989, Beck et al. 1994, Kulsrud et al. 1997), they have attracted surprisingly little attention in studies of primordial star formation. Over the past couple of years, however, this has begun to change, with several recent studies focussing on the growth of magnetic fields during the formation of the first stars. The first of these was Schleicher et al. (2010), who studied the effectiveness of the turbulent dynamo during gravitational collapse using a simple one-zone Lagrangian model for the collapsing gas. Their model assumes that turbulence is generated by gravitational collapse on a scale of the order of the Jeans length, and that on smaller scales, the Jeans length turbulent velocity scales with the length-scale l as v_turb l. Schleicher et al. (2010) study both Kolmogorov turbulence, with = 1/3 and Burgers turbulence, with = 1/2, and show that in both cases, amplification of a weak initial seed field occurs rapidly, and that the field reaches saturation on all but the largest scales at an early point during the collapse. Because Schleicher et al. (2010) did not solve directly for the fluid velocities, they were unable to model the approach to saturation directly. Instead, they simply followed Subramanian (1998) and assumed that the strength of the saturated field satisfies

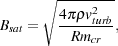(59)

where Rm_cr ~ 60 is a critical value of the magnetic Reynolds number, Rm = v_turb l / (where is the resistivity), that must be exceeded in order for exponential growth of the field to occur (Subramanian 1998).

The main weakness of the Schleicher et al. (2010) study lies in the assumptions that it was forced to make about the nature of the turbulent velocity field. Therefore, in a follow-up study, Sur et al. (2010) used high-resolution adaptive mesh refinement simulations to directly follow the coupled evolution of the velocity field and the magnetic field within a 3D collapse model. For their initial conditions, Sur et al. (2010) took a super-critical Bonnor-Ebert sphere (Bonnor 1956, Ebert 1955) with a core density n_c = 10⁴ cm^-3 and a temperature T = 300 K. They included initial solid-body rotation, with a rotational energy that was 4% of the total gravitational energy, and a turbulent velocity component with an RMS velocity equal to the sound speed and with an energy spectrum E(k) k^-2. A weak magnetic field was also included, with an RMS field strength B_rms = 1 nG, and with the same energy spectrum as the turbulence. For reasons of computational efficiency, Sur et al. (2010) did not follow the thermal and chemical evolution of the gas directly. Instead, they adopted a simple barotropic equation of state, P ^1.1, inspired by the results of previous hydrodynamical models (e.g. Abel, Bryan & Norman 2002). In view of the sensitivity of the turbulent dynamo to the Reynolds number, and the fact that numerical dissipation on the grid scale limits the size of Re in any 3D numerical simulation to be substantially less than the true physical value, there is good reason to expect that the dynamo amplification rate will be sensitive to the numerical resolution of the simulation. Sur et al. (2010) therefore focussed on the effects of resolution, performing five different simulations with the same initial conditions, but with different grid refinement criteria. Starting with a model in which the refinement criterion ensures that the Jeans length is always resolved Jeans length by 8 grid zones, they looked at the effects of increasing this number to 16, 32, 64 and 128 grid zones.

Sur et al. (2010) showed that in the 8 and 16 cell runs, the magnetic field strength increases with density at a slower rate than the B ^2/3 that we would expect simply from flux freezing and roughly spherical collapse, indicating that in these runs, the turbulent dynamo does not operate. Starting with the 32 cell run, however, they found evidence for an increase in B with density that is larger than can be explained simply by compression, which they ascribe to the effects of the turbulent dynamo. They showed that as the number of grid zones used to resolve the Jeans length Jeans length is increased, the rate at which the field grows also increases, and there is no sign of convergence at even their highest resolution. This resolution dependence explains why the earlier study of Xu et al. (2008) found no evidence for dynamo amplification, as their study used only 16 grid zones per Jeans length.

More recently, Federrath et al. (2011) have re-examined this issue of resolution dependence, and have shown that when the number of grid zones per Jeans length is small, the amount of turbulent Jeans length energy on small scales is also significantly underestimated. The reason for this is the same as the reason for the non-operation of the turbulent dynamo: the effective Reynolds number is too small. Federrath et al. (2011) show that in gravitationally collapsing regions that undergo adaptive mesh refinement, the effective Reynolds number scales with the number of grid zones per Jeans length as Re_eff = (N / 2)^4/3. Furthermore, an effective Reynolds number Re_eff ~ 40 is required in order for the turbulent dynamo to operate, implying that one needs N ~ 30 or more zones per Jeans length in order to begin resolving it, in agreement with the findings of Sur et al. (2010). It should also be noted that the operation of the turbulent dynamo in simulations of turbulence without self-gravity requires a similar minimum value for the Reynolds number (Haugen, Brandenburg & Dobler 2004).

Together, these studies support the view that amplification of a weak initial magnetic field by the turbulent dynamo may indeed have occurred within the first star-forming minihalos. However, a number of important issues remain to be addressed. First, the three-dimensional studies carried out so far all adopt a simple barotropic equation of state, rather than solving self-consistently for the thermal evolution of the gas. This is a useful simplifying assumption, but may lead to incorrect dynamical behaviour, as one misses any effects due to thermal instabilities, or the thermal inertia of the gas (i.e. the fact that the cooling time is typically comparable in size to the dynamical time). Work is currently in progress to re-run some of these models with a more realistic treatment of the thermodynamics and chemistry in order to explore the effect that this has on the degree of amplification (T. Peters, private communication). Second, it will clearly be important to perform similar studies using more realistic initial conditions for the gas. Of particular concern is whether the turbulence that is generated during the gravitational collapse of gas within a primordial minihalo is similar in nature to that studied in these more idealized calculations, and if not, what influence this has on the amplification of the field. Finally, and most importantly, there is the issue of the level at which the field saturates. Exponential amplification of the field by the small-scale dynamo will occur only while the kinematic approximation holds, i.e. while the energy stored in the magnetic field is much smaller than the energy stored in the small-scale turbulent motions. Once the field becomes large, the Lorentz force that it exerts on the gas will act to resist further folding and amplification of the field. In addition, the dissipation of magnetic energy by Ohmic diffusion and ambipolar diffusion will grow increasingly important. However, it remains unclear which of these effects will be the most important for limiting the growth of the magnetic field in dense primordial gas.

2.3.3. Consequences

If a strong magnetic field can be generated by dynamo amplification, then it will affect both the thermal and the dynamical evolution of the gas. The possible dynamical effects of a strong magnetic field have been investigated by Machida et al. (2006), Machida et al. (2008). In a preliminary study, Machida et al. (2006) used nested-grid simulations to investigate the influence of a magnetic field on the collapse of a small, slowly-rotating primordial gas cloud. For their initial conditions, they used a supercritical Bonnor-Ebert sphere with mass 5.1 × 10⁴ M, radius 6.6 pc, central density n_c = 10³ cm^-3 and an initial temperature of 250 K. They assumed that this cloud was in solid body rotation with angular velocity ₀ and that it was threaded by a uniform magnetic field oriented parallel to the rotation axis, with an initial field strength B₀. They performed simulations with several different values of ₀ and B₀, with the former ranging from 10^-17 s^-1 to 3.3 × 10^-16 s^-1, and the latter from 10^-9 G to 10^-6 G. To treat the thermal evolution of the gas, they used a barotropic equation of state, based on the one-zone results of Omukai et al. (2005).

Machida et al. (2006) used this numerical setup to follow the collapse of the gas down to scales of the order of the protostellar radius. They showed that the magnetic field was significantly amplified by compression and flux freezing during the collapse, reaching strengths of order 6 × 10⁵-6 × 10⁶ G on the scale of the protostar. A very compact disk with a radius of few R formed around the protostar, and in models with initial field strength B₀ > 10^-9 G, the magnetic field became strong enough to drive a hydromagnetic disk wind that ejected roughly 10% of the infalling gas. Numerical limitations (discussed in Section 3 below) prevented Machida et al. (2006) from following the evolution of the system for longer than a few days after the formation of the protostar, and so it remains unclear whether an outflow would eventually be generated in the 10^-9 G case, and whether the outflows continue to be driven as the protostar and disk both grow to much larger masses.

In a follow-up study, Machida et al. (2008) used a similar numerical setup, but examined a much broader range of values for ₀ ( E_rot / |E_grav|), the ratio of the initial rotational energy to the initial gravitational energy, and ₀ ( E_mag / |E_grav|), the ratio of the initial magnetic energy to the initial gravitational energy. They found that the outcomes of the simulations could be classified into two main groupings. Clouds with ₀ > ₀, i.e. ones which were rotationally dominated, formed a prominent disk during the collapse that then fragmented into a binary or higher order multiple system. In these simulations, no jets were seen (with the exception of a couple of model in which ₀ ~ ₀). On the other hand, when ₀ < ₀, i.e. when the cloud was magnetically dominated, the disk that formed was much less prominent and did not fragment, but instead an outflow was driven that removed of order 10% of the gas that reached the disk, as in the Machida et al. (2006) study.

These results support the idea that outflows will be a natural consequence of the generation of strong magnetic fields during Population III star formation. However, it is important to note that the Machida et al. (2006), Machida et al. (2008) simulations only model the very earliest stages of outflow driving, on a timescale t ≪ 1 yr. The evolution of outflows on much longer timescales, and their influence on the infalling gas have not yet been studied in detail, and it is unclear to what extent one can safely extrapolate from the very limited period that has been studied.

A strong magnetic field could also have a direct impact on the thermal evolution of the gas, through the heating arising from ambipolar diffusion. The effects of this process in gravitationally collapsing gas within the first star-forming minihalos have been investigated by Schleicher et al. (2009) using a simple one-zone treatment of the gas. They assume that in the absence of ambipolar diffusion, the magnetic field strength would evolve as B , where = 0.57 (M_J / M_{J, mag})^0.0116 and M_{J, mag} is the magnetic Jeans mass (i.e. the minimum mass that a perturbation must have Jeans mass!magnetic in order to be unstable to its own self-gravity when support against collapse is provided by a magnetic field, rather than by thermal pressure). This expression for is an empirical fitting formula derived by Schleicher et al. (2009) from the results of Machida et al. (2006). In their treatment of the evolution of B within their one-zone models, Schleicher et al. (2009) also account for the loss of magnetic energy through ambipolar diffusion.

Another important simplification made in the Schleicher et al. (2009) model is the replacement of the full expression for the ambipolar diffusion heating rate (Pinto et al. 2008)

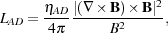(60)

where B = |B| and _AD is the ambipolar diffusion resistivity, with the simpler approximation

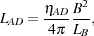(61)

where L_b is the coherence length of the magnetic field.

Schleicher et al. (2009) show that if the initial field strength is less than 0.01 nG (comoving), then ambipolar diffusion heating has almost no effect on the thermal evolution of the gas. For stronger fields, ambipolar diffusion heating leads to an increase in the gas temperature at densities between n ~ 10⁴ cm^-3 and n ~ 10¹⁰ cm^-3, amounting to as much as a factor of three at n ~ 10⁸ cm^-3. However, at higher densities, three-body H₂ formation heating becomes a more important heat source than ambipolar diffusion, meaning that the temperature evolution becomes largely independent of the magnetic field strength once again. Schleicher et al. (2009) did not examine initial field strengths larger than 1 comoving nG, as these are ruled out by observational constraints, but if one considers the effects of the turbulent dynamo acting during the collapse, then it is possible that much larger fields could be generated on smaller scales, and it would be useful to revisit this issue and examine whether ambipolar diffusion heating from these smaller-scale fields can significantly affect the collapse of the gas.

Finally, one important caveat to bear in mind regarding the Machida et al. (2006), Machida et al. (2008) and Schleicher et al. (2009) simulations is the fact that they adopt a correlated initial magnetic field, while the field generated by the turbulent dynamo will have little or no correlation on large scales (Maron, Cowley & McWilliams 2004). The extent to which the dynamical and thermal effects of this uncorrelated field will be the same as those of a correlated field is unclear. Further investigation of this issue would be very valuable.

³ Discussions of Population III star formation often refer to the cold clump of gas at the centre of the minihalo as a "fragment", and speak of M_BE as the "fragmentation mass scale", but in the case of the very first generation of star-forming minihalos, this is actually something of a misnomer, as very seldom does more than one "fragment" form in a given minihalo Back.

⁴ A similar process can also occur during collisions of atomic hydrogen or atomic helium with H₂, but it is the H₂-H₂ case that is the most relevant here Back.