3. EVOLUTION AFTER THE FORMATION OF THE FIRST PROTOSTAR

As we saw in the last section, when it comes to the formation of the very first Population III protostar, there is broad agreement on the details of the process, with different groups, who use different numerical approaches, finding results that are in good qualitative agreement with each other. Some quantitative disagreements still exist (see e.g. Turk et al. 2011), but it is unclear to what extent these reflect real differences between numerical approaches as opposed to natural variation in the details of the collapse. The main uncertainties in this phase stem from uncertainties in the input physics, such as whether magnetic fields can become amplified to dynamically significant levels during the collapse, or whether dark matter annihilation significantly affects the outcome.

Once we move on to considering the evolution of the gas within star-forming minihalos after the formation of the first protostar, the situation becomes much less clear. The fundamental problem stems from the fact that although we can follow the gravitational collapse of the primordial gas down to scales as small as the protostellar radius (see e.g. Yoshida, Omukai & Hernquist 2008), the numerical timestep in an explicit hydrodynamical code becomes extremely short during this process. This is a consequence of the Courant condition, which states that for such a code to be numerically stable, the timestep must satisfy

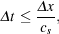(62)

where x is the size of the smallest resolution element, and c_s is the sound speed of the gas.

The Courant condition implies that if we take a value of x small enough to adequately resolve the structure of the protostar and the gas immediately surrounding it (e.g. x = 1 R), then the required timestep will be extremely small: t 7 × 10⁴ s for x = 1 R and a sound speed of 10 km s^-1. This means that if we want to follow the later evolution of the protostar and the surrounding gas over a timescale of thousands of years in order to see how it grows in mass prior to reaching the main sequence, then we must use a very large number of timesteps: our simple estimate above yields a number of the order of a million. In practice, the computational expense of doing this within a three-dimensional hydrodynamical code is prohibitively large, meaning that it has so far proved impossible to study the evolution of the gas in this fashion.

Efforts to surmount this difficulty typically follow one of two approaches. One approach is simply to halt the numerical simulation at the point at which the Courant timestep becomes prohibitively small, and to model the later evolution of the protostar using a semi-analytical, or one-dimensional, fully numerical treatment. To do this, it is necessary to make some assumption about the behaviour of the gas surrounding the protostar. In general, models of this type assume that the gas does not fragment and form additional protostars, but instead is simply accreted by the existing protostar, either directly or via a protostellar accretion disk. The results obtained using this approach - what we afterwards refer to as the "smooth accretion model" - are discussed in Section 3.1 below.

The other approach that can be used to study the further evolution of the gas surrounding the protostar makes use of a technique developed for studies of contemporary star formation, which face a similar problem on protostellar scales. Gravitationally bound regions of gas that become smaller than some pre-selected size scale are replaced by what are usually termed sink particles (see e.g. Bate, Bonnell & Price 1995). These particles can accrete gas from their surroundings and continue to interact gravitationally with the surrounding gas, but allow one to neglect the very small-scale hydrodynamical flows that would otherwise force one to take very small numerical timesteps owing to the Courant condition. The great advantage of the sink particle technique is that one need make no assumption about the dynamical evolution of the gas surrounding the protostar on scales much larger than the effective size of the sink particle (the so-called accretion radius, discussed in more detail below), as one can simply continue to model this using the same numerical techniques as were used to model the initial gravitational collapse. The main disadvantage of the technique is that, strictly speaking, it represents an ad hoc modification of the fluid equations, with consequences that may not be entirely straightforward to predict. The modification to the solution caused by replacing dense gas with sink particles is unlikely to significantly affect the evolution of the gas on scales that are much larger than the accretion radius, but will clearly have an effect on the flow on scales close to the accretion radius. In addition, the common strategy of treating sink particles as point masses may not be appropriate when dealing with close encounters between sinks, as one misses the tidal forces acting between the gas clumps represented by the sinks.

Although sink particles have been used in studies of Population III star formation for over a decade, simulations using the correct initial conditions, and with sufficient spatial resolution and mass resolution to capture the details of the gas flow on scales close to those of individual protostars have only recently become possible. These simulations show that, contrary to the assumption made in the smooth accretion model, the gas generally fragments, rather than simply accreting onto a single, central protostar. The results obtained from studies using sink particles - afterwards referred to as the "fragmentation model" for Population III star formation - are discussed in Section 3.2 below.

3.1. The smooth accretion model

3.1.1. Determining the accretion rate

As we have already discussed above, at the point at which the protostar forms, its mass is very small (M ~ 0.01 M; see Yoshida, Omukai & Hernquist 2008), but it is surrounded by an infalling envelope of gas containing tens or hundreds of solar masses. If we assume that the gas in this infalling envelope does not undergo gravitational fragmentation, then it has only two possible fates - it must either be accreted by the central protostar (or protostellar binary; see e.g. Turk, Abel & O'Shea 2009), or it must be prevented from accreting, and possibly expelled from the immediate vicinity of the protostar, by some form of protostellar feedback. This means that the mass of the protostar at the point at which it forms has very little to do with its final mass. To determine the size of the latter, we must understand the rate at which gas is accreted by the protostar, and how this process is affected by protostellar feedback.

Since protostellar feedback involves a number of different processes, many of which are complicated to model, it is easiest to start by considering models in which feedback effects are not included. As feedback acts to reduce the accretion rate, models of this type allow us to place an upper limit on the final mass of the Pop. III star.

A useful starting point is a simple dimensional analysis. Suppose that the protostar is embedded in a gravitationally unstable cloud of mass M and mean density < >, and that the protostellar mass M_* ≪ M, so that its gravity is negligible in comparison to the self-gravity of the cloud. The timescale on which the gas cloud will undergo gravitational collapse and be accreted by the protostar is simply the free-fall collapse time, t_ff = (3 / 32 G < >)^1/2. Therefore, the time-averaged accretion rate will be given approximately by

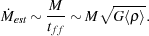(63)

If the gas cloud were highly gravitationally unstable, then it would fragment rather than accreting onto a single object, so let us assume that it is only marginally unstable, i.e. that M ~ M_J. In that case, since M_J ~ c_s³ G^{-3/2 -1/2}, we can write our estimate of the time-averaged accretion rate as

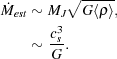(64) (65)

We therefore find that the characteristic accretion rate scales as the cube of the sound speed. Moreover, since c_s T^1/2, this implies that the accretion rate scales with temperature as T^3/2.

This is an important result, because as we have already seen, the characteristic temperature of the dense, star-forming gas in a primordial minihalo is of the order of 1000 K, far larger than the 10 K temperatures found within prestellar cores in local regions of star formation (see e.g. Bergin & Tafalla 2007). Our simple scaling argument therefore tells us that we will be dealing with far higher accretion rates in the Population III case than we are used to from studies of local star formation.

If we want to improve on this simple scaling argument and derive a more accurate figure for the accretion rate, then there are three main ways in which we can go about it. One possible approach is to construct a simplified model for the collapsing protostellar core from which an approximation to the true accretion rate can be derived analytically (or with only minor use of numerical calculations). For example, if we assume that the protostellar core is isothermal and spherically symmetric, then there is a whole family of similarity solutions that could potentially be used to describe the collapse (Hunter 1977, Whitworth & Summers 1985), including the familiar Larson-Penston solution (Larson 1969, Penston 1969), or the Shu solution (Shu 1977).

An example of this approach is given in Omukai & Nishi (1998). These authors used a spherically symmetric Lagrangian hydrodynamical code to simulate the formation of a Population III protostar, and found that prior to core formation, the gravitational collapse of the gas could be well described with a Larson-Penston similarity solution, with an entropy parameter K = p / = 4.2 × 10¹¹ (in cgs units) and an effective adiabatic index _eff = 1.09. Omukai & Nishi (1998) were unable to continue their numerical study past the point at which the protostar formed, for the reasons addressed above, but assumed that the same similarity solution would continue to apply. By making this assumption, they were therefore able to derive the following accretion rate for the protostar

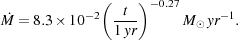(66)

In a similar study, using a more sophisticated treatment of the microphysics of the collapsing gas, Ripamonti et al. (2002) also found that the initial flow was well described as a Larson-Penston similarity solution, but derived a different accretion rate

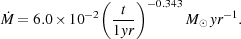(67)

Another example of this approach comes from Tan & McKee (2004). They model the accretion flow onto a Pop. III protostar as a spherical, isentropic polytrope, and derive an accretion rate that is a function of three parameters: the entropy parameter K, the polytropic index _p (which, for an isentropic flow, is equal to the adiabatic index ), and _*, a numeric parameter of order unity, which is related to the initial conditions of the flow. Tan & McKee (2004) use the results of Omukai & Nishi (1998) and Ripamonti et al. (2002) to argue that _p = 1.1, and use the 3D simulation results of Abel, Bryan & Norman (2002) to set the other two parameters to _* = 1.43 and K = 1.88 × 10¹² K' (in cgs units), where

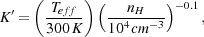(68)

and where the effective temperature T_eff = P_eff / (nk) accounts for the contribution made to the pressure by small-scale, subsonic turbulence in addition to the standard thermal pressure. Based on this, they then derive the following rate for the accretion of gas onto the protostar and its associated accretion disk

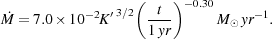(69)

This can be directly compared to the other determinations of if we assume that all of the gas reaching the accretion disk is eventually accreted by the star, which is a reasonable assumption for models that do not include the effects of gravitational fragmentation or protostellar feedback.

Instead of using simulation results to select a particular collapse model (e.g. Larson-Penston collapse) and then calculating from the model, the second main approach used to determine attempts to infer it from the state of the gas in the simulation at the point at which the protostar forms, using the information that the simulation provides on the density and velocity distributions of the gas. This approach was pioneered by Abel, Bryan & Norman (2002), who considered two simple models for the time taken for a given fluid element to accrete onto the central protostar. In the first of these models, they assumed that the time taken for the gas within a spherically-averaged shell of radius r to accrete onto the protostar was given by the ratio between the mass enclosed within the shell, M(r), and the rate at which gas was flowing inward at that radius, i.e.

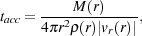(70)

where (r) and v_r(r) are the spherically-averaged density and radial velocity in the shell. In the second model for t_acc, they used an even simpler approximation, setting t_acc to the time that it would take for the gas to reach the protostar if it merely maintained its current radial velocity, i.e.

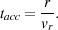(71)

Abel, Bryan & Norman (2002) show that other than at the very earliest times, these two approaches yield very similar values for t_acc, and hence very similar values for the accretion rate. This strategy has subsequently been used by many other authors to derive predicted protostellar accretion rates from their simulations (see e.g. Yoshida et al. 2006, O'Shea & Norman 2007, McGreer & Bryan 2008, Turk et al. 2011). Of particular note is the study by O'Shea & Norman (2007), who perform multiple simulations of Population III star formation using different random realizations of the cosmological density field. They find that minihalos assembling at higher redshifts form more H₂ than those assembling at lower redshifts, owing to the higher mean density of the virialized gas in the high redshift minihalos. They show that in their simulations, this leads to the gas at densities n > 10⁴ cm^-3 having significant differences in its mean temperature in the different halos. In the most H₂-rich minihalos, the dense gas can be as cold as 200 K, while in the minihalos with the least H₂, it can be as high as 1000 K. As a result, the predicted accretion rates for the different minihalos span more than an order of magnitude, thanks to the strong scaling of with temperature. Unfortunately, it is necessary to treat these results with a degree of caution, as the O'Shea & Norman (2007) simulations did not include the effect of three-body H₂ formation heating, which is known to have a significant influence on the temperature of the dense gas. It is unclear whether simulations that include this effect would produce dense gas with such a wide range of temperatures and accretion rates, although a study that is currently being carried out by Turk and collaborators should address this issue in the near future (M. Turk, private communication).

The third main approach used to determine the accretion rate involves measuring it directly in a simulation of the later evolution of the gas around the protostar. If we replace the protostar with a sink particle, then we can measure simply by measuring the rate at which the sink particle mass increases. This approach was first used by Bromm & Loeb (2004), in a study of Population III star formation in which a sink particle was created once the gas density exceeded a threshold value n_th = 10¹² cm^-3 (we will have more to say about this study below). Bromm & Loeb (2004) showed that the rate at which gas was accreted by the sink particle could be approximated as a broken power-law

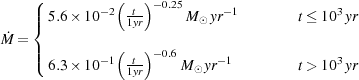(72)

for times t < 10⁴ yr. Bromm & Loeb halted their simulation at t ~ 10⁴ yr and hence could not directly measure the evolution of at later times, although they did consider what the final mass of the protostar would be if one simply extrapolated Equation 72 over the three million year lifetime of a massive star.

Accretion rates have also been measured using the sink particle technique in the group of simulations carried out by Clark et al. (2011a, 2011b), Greif et al. (2011a) and Smith et al. (2011) that find evidence for fragmentation of the gas (see Section 3.2 below). The accretion rates onto the individual sinks show a considerable degree of variability in these calculations, but the total accretion rate, i.e. the rate of change of the sum of all of the sink particle masses, evolves more smoothly with time, and is of a similar order of magnitude to the other estimates plotted above.

In Figure 3 we compare several of these different estimates for the accretion rate. We plot three examples, derived using different techniques: a rate based on the Tan & McKee (2004) formalism, computed assuming that K' = 1; a rate inferred from the results of one of the adaptive mesh refinement simulations presented in Turk et al. (2011) - specifically, the simulation that was run using the Palla, Salpeter, & Stahler (1983) rate coefficient for three-body H₂ formation; and a rate measured using sink particles, taken from Smith et al. (2011).

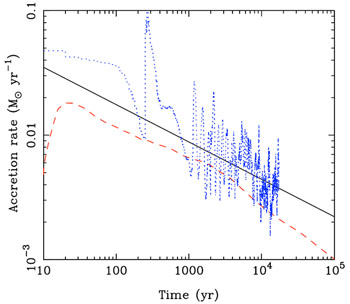Figure 3. Three different estimates for the accretion rate onto a Pop. III protostar, taken from Tan & McKee (2004; solid line), Turk et al. (2011; dashed line) and Smith et al. (2011; dotted line), as described in the text. Results from the Smith et al. (2011) simulation are only plotted for the period covered by the simulation, i.e. t < 2 × 104 yr.

At very early times (t < 100 yr), the three different techniques yield rather different estimates for , but this is primarily a consequence of the limited resolution of the numerical simulations. At later times, we see that both the Tan & McKee (2004) formalism and the Turk et al. (2011) simulation predict a similar form for the accretion rate, but disagree by about a factor of two on the normalization, which may simply indicate that our adopted value of K' is slightly too large. We also see the same general trend in the Smith et al. (2011) results, but in this case there is considerable and rapid variation in with time. This is a result of the fragmentation of the gas in this simulation, which produces a set of sink particles that undergo chaotic N-body interactions (see Section 3.2 below). A similar effect is seen in simulations of protostellar accretion in present-day star-forming regions (see e.g. Stamatellos, Whitworth & Hubber 2011).

Regardless of whether varies smoothly or erratically with time, one fact that is clear from Figure 3 is that the protostellar accretion rate remains very large for a considerable time. This implies that the total mass of gas that is converted to stars can become fairly large after a relatively short time. For example, if we take the Tan & McKee (2004) estimate with K' = 1 as a guide, then we find that the total mass in stars increases with time as:

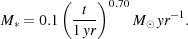(73)

This means that after 5 × 10⁴ yr (the Kelvin-Helmholtz relaxation time for a 100 M star), we have M_* 195 M, while after 2 × 10⁶ yr (the typical lifetime for an O star), we have M_* 2575 M. Therefore, if the gas does not fragment and protostellar feedback is ineffective, one is led to the prediction that the resulting Population III star will be extremely massive. In practice, the gas probably does fragment (see Section 3.2 below), and protostellar feedback cannot be completely ignored, but even so, we would expect to be able to form massive Population III stars relatively easily.

Finally, it should be noted that so far we have considered accretion only in the standard H₂-dominated case, i.e. in a minihalo with a minimum gas temperature of around 200 K. In minihalos that reach much lower temperatures through HD cooling, the predicted accretion rates are smaller, as one would expect from the simple dimensional analysis given at the start of this section. For example, if one uses the Tan & McKee (2004) formalism to estimate the accretion rate, then Equation 69 still applies, but the value of K' is significantly smaller. Taking n = 10⁶ cm^-3 and T_eff = 150 K as plausible values to substitute into Equation 68, we find that K' 0.3, and hence the predicted accretion rate is roughly a factor of six smaller than in the H₂-dominated case. Values estimated from numerical simulations using the Abel, Bryan & Norman (2002) approach agree fairly well with this simple estimate (see e.g. Yoshida, Omukai & Hernquist 2007, McGreer & Bryan 2008).

3.1.2. Protostellar structure and evolution

Having established how quickly gas will be accreted by the protostar in the absence of feedback, the obvious next step is to examine how this will be modified by protostellar feedback. Before doing this, however, we must first spend a little time discussing what is known about the internal structure of Population III protostars, and how this evolves with time. This is important if we want to understand how the radius and luminosity of a given Pop. III protostar evolve, and these quantities are obviously of great importance when determining the influence of that protostar on the surrounding gas.

The internal structure of a Pop. III protostar, and how this evolves as the protostar ages and accretes matter from its surroundings was first studied in detail by Stahler, Palla & Salpeter (1986a, 1986b). They assume that the accretion process can be treated as a series of quasi-steady-state accretion flows onto a hydrostatic core, which is bounded by a strongly radiating accretion shock. Within the core, the standard stellar structure equations are solved. Outside of the core, the treatment depends on the optical depth of the gas. If the gas is optically thin to the radiation from the accretion shock, then the accretion flow is assumed to be in free-fall. Otherwise, a more detailed calculation is made that incorporates the effects of the radiation force on the infalling gas. The accretion shock itself is treated as a simple discontinuity.

In their initial study, Stahler, Palla & Salpeter (1986a) began with a core mass of 0.01 M and followed the growth of the protostar until its mass reached 10.5 M. They assumed a constant accretion rate = 4.41 × 10^-3 M yr^-1, and found that for this choice of accretion rate, the evolution of the protostar could be divided into three qualitatively distinct phases.

In the first phase, which lasts until the protostellar mass M_* = 0.1 M, the protostar relaxes from its initial entropy profile into one consistent with the selected accretion rate. Stahler, Palla & Salpeter (1986a) dub this a 'decay of transients' phase, and the fact that it quickly comes to an end shows that although the initial conditions used in the Stahler, Palla & Salpeter (1986a) study are probably incorrect in detail, the flow soon loses all memory of them, and therefore any inaccuracy at this stage is unlikely to affect the later results.

Once the initial transients have died away, the protostar enters the second phase of its evolution. During this phase, its central temperature remains low (T_c ~ 10⁵ K), resulting in a high interior opacity and hence a low interior luminosity. Consequently, the evolution of the core during this phase is almost adiabatic; although the core continues to gradually contract, this contraction does not lead to any increase in the central entropy. Since the postshock entropy increases over time due to the increasing strength of the accretion shock (which is itself a natural result of the increasing protostellar mass), the core develops an off-centre distribution of entropy and temperature.

The gas surrounding the accretion shock remains optically thick throughout this period. This is a direct result of the high accretion rate, which produces a highly luminous accretion shock. This produces sufficient radiation to partially ionize the preshock gas in the vicinity of the shock, creating a structure known as a radiative precursor. The H^- opacity of the dense, partially ionized gas in this radiative precursor is more than sufficient to make it optically thick. Stahler, Palla & Salpeter (1986a) show that the core radius during this period evolves as

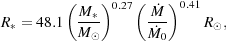(74)

where ₀ = 4.41 × 10^-3 M yr^-1, while the photospheric radius evolves as

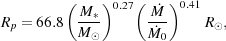(75)

so R_p > R_* throughout. The strong H^- opacity also keeps the photospheric temperature low (T_p ~ 6000 K), which prevents the protostar from being able to ionize material outside of its photosphere.

This near-adiabatic accretion phase comes to an end once the cooling time of the core, given approximately by the Kelvin-Helmholtz timescale Kelvin-Helmholtz time

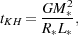(76)

becomes comparable to the accretion timescale t_acc = M_* / . This occurs for a core mass M ~ 1 M, and results in the core entering a phase of homologous collapse, while energy and entropy are transferred outwards in the form of a `luminosity wave'. The radial position of the luminosity peak moves outwards towards the accretion shock, reaching it at about the time that the core mass has reached 8 M. This results in a rapid swelling of the outermost layers, which weakens the accretion shock and leads to it becoming optically thin. sps86a terminate their simulation shortly afterwards, once the core mass has reached 10.5 M.

Stahler, Palla & Salpeter (1986b) simulate the later stages of the evolution of a primordial protostar. Their initial protostellar core has a mass of 5 M, and they evolve this core forward in time, assuming that no further accretion occurs (i.e. the protostellar mass remains fixed at 5 M). They find that deuterium burning within the protostar begins after only 6000 years, but that hydrogen ignition does not occur until t = 2 × 10⁵ yr, and the protostar does not reach the zero-age main sequence (ZAMS) until t ~ 10⁶ yr.

An improved treatment of the later stages of the evolution of the protostar was made by Omukai & Palla (2001). They used a very similar setup to that in Stahler, Palla & Salpeter (1986a), albeit with improved zero metallicity opacities, and adopted the same constant accretion rate, = 4.41 × 10^-3 M yr^-1. However, unlike Stahler, Palla & Salpeter (1986a), they initialized their simulation at the point at which the core mass was M = 8 M, but did not halt the simulation once the core had grown to 10.5 M. Instead, they continued to follow the growth of the protostar until well after hydrogen ignition. They found that deuterium burning within the core began once the core mass was 12 M (corresponding to a time t = 1000 yr after the beginning of the simulation, given the assumed accretion rate), and that it was complete by the time the mass had reached 30 M (corresponding to t = 5000 yr). Hydrogen ignition followed roughly 11000 years later, at t = 1.6 × 10⁴ yr after the beginning of the simulation, at which time the mass of the protostar was 80 M. At this point, the internal luminosity of the protostar is very close to the Eddington value, which leads to the outer layers of the protostar developing oscillatory behaviour: the high luminosity leads to expansion, the expansion causes the accretion luminosity to drop, the reduced luminosity can no longer maintain the expansion, leading to contraction of the core, and the contraction raises the accretion luminosity, allowing the whole cycle to begin again. Finally, once the core mass reaches 300 M, at t ~ 6.6 × 10⁴ yr, the contribution of nuclear burning to the protostellar luminosity becomes large enough to drive a final phase of expansion that is strong enough to terminate accretion onto the protostar. Omukai & Palla (2001) halt their simulation at this point.

In a follow-up study using a similar spherically-symmetric setup, Omukai & Palla (2003) performed the same analysis for a range of different values of , looking at models with = (0.25, 0.5, 1.0, 2.0) × _fid (where _fid was the rate adopted by Stahler, Palla & Salpeter 1986a and Omukai & Palla 2001), as well as a model using the time-dependent accretion rate predicted by Abel, Bryan & Norman (2002). The earliest stages of protostellar evolution are qualitatively the same in all of these models: we see again the same sequence of adiabatic growth, propagation of a luminosity wave that triggers expansion of the outer layers, and then rapid contraction. Although some quantitative differences are apparent, significant differences in behaviour do not occur until the end of the contraction phase. At this point, the further evolution of the protostar is governed by the size of the accretion rate. For accretion rates greater than some critical value _crit, the luminosity of the protostar becomes large enough to halt the accretion. On the other hand, for < _crit, the lower accretion luminosity means that the total luminosity of the protostar remains below L_Edd, and accretion continues unabated.

Omukai & Palla (2003) solve for _crit by equating the total luminosity of a zero-age main sequence Pop. III protostar (including accretion luminosity) with the Eddington luminosity, and find that

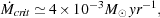(77)

coincidentally close to _fid. In principle, one would expect _crit to have a dependence on the current mass of the protostar, but in practice, Omukai & Palla (2003) show that this dependence is weak and may be neglected.

Finally, Omukai & Palla (2003) show that in the time-dependent accretion model, the key factor is the size of the accretion rate at the end of the contraction phase. If this is greater than _crit, then one would expect accretion to be halted, while if it is less than _crit then accretion can continue. In practice, Omukai & Palla (2003) show that if one adopts the Abel, Bryan & Norman (2002) estimated accretion rate, then < _crit, implying that accretion can continue even once the protostar reaches the zero-age main sequence.

The main limitation of the approach outlined above is the neglect of the effects of rotation. In reality, rotation can have profound effects on stellar structure and evolution, particularly for massive stars (Maeder & Meynet 2000), and it will also have a large influence on how matter reaches the protostar in the first place. The first detailed study of the pre-main sequence evolution of a Pop. III protostar to account for the effects of rotation was carried out by Tan & McKee (2004). In contrast to previous authors, they did not assume spherical symmetry. Instead, they assumed that a protostellar accretion disk would form, and fixed the size of the disk by assuming angular momentum conservation within the supersonic portion of the accretion flow. They used the polytropic accretion flow model described in the previous section to compute the accretion flow onto the disk. To solve for the disk structure, they made use of the standard theory of steady, thin viscous accretion disks (as outlined in Shakura & Sunyaev 1973), with a spatially constant viscosity parameter . As sources for , they considered the magnetorotational instability (Balbus & Hawley 1991, Balbus & Hawley 1998) and gravitational instability. With the disk structure in hand, they could then solve for the structure of the protostar itself, using a modified version of an approach developed by Nakano, Hasegawa & Norman (1995) and Nakano et al. (2000). In the zero angular momentum case, Tan & McKee (2004) show that they successfully reproduce the previous results of Stahler, Palla & Salpeter (1986a) and Omukai & Palla (2001), Omukai & Palla (2003). In more realistic models, Tan & McKee (2004) show that the presence of an accretion disk has little influence on the evolution of the protostar, which still evolves through the same progression of adiabatic growth, terminated by the emergence of a luminosity wave, followed by rapid contraction to the ZAMS. However, Tan & McKee (2004) do find that the photosphere surrounding the protostar behaves very differently in this case than in the spherical case. Because most of the gas accretes onto the protostar via the disk, the gas density is significantly reduced in the polar regions. Consequently, the optical depth of these regions is also significantly reduced, with the result that the flow becomes optically thin early in its evolution. For example, in the model with f_Kep = 0.5, the photosphere vanishes once the protostellar mass reaches 1 M and does not subsequently reappear. Tan & McKee (2004) argue that this may have a major influence on the effectiveness of radiative feedback from the protostar, a topic that we will return to in the next section.

3.1.3. Feedback effects

Accretion of gas onto the protostar liberates a significant amount of energy, with most of this energy being emitted from regions close to the protostellar surface. This can be shown very simply by considering how the gravitational potential energy of a test mass changes as we move it close to a protostar of mass M_* and radius R_*. At a distance of 2R_*, the gravitational potential energy of a fluid element with mass dM is

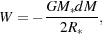(78)

while at the protostellar surface it is

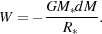(79)

Therefore, the amount of energy that must be dissipated by the fluid element as it moves from 2R_* to R_* is as large as the amount that it must have dissipated while falling in from R ≫ R_* to 2R_*, or in other words, half of the total binding energy dissipated by the gas is dissipated while its distance from the protostellar surface is less than R_*. In addition, once the protostar reaches the main sequence, it will start generating additional energy in its own right, via nuclear fusion. The energy that is released in the vicinity of the protostar is therefore quite considerable, and it is reasonable to suppose that this will have some effect on the behaviour of the surrounding gas. It is therefore not surprising that considerable attention has been paid to the issue of protostellar feedback in the context of Pop. III star formation.

In order for the protostar to substantially reduce the rate at which matter flows onto it, it must be able to transfer a significant amount of energy and/or momentum to the infalling gas. The various mechanisms by which this can be accomplished fall under two broad headings: mechanical feedback, where the protostar transfers energy and momentum to some form of outflow, which subsequently transfers it to the infalling material, and radiative feedback, where radiation from the protostar transfers energy and momentum directly to the infalling gas.

Mechanical feedback

In the local Universe, stellar winds are an almost ubiquitous phenomenon, and play an important role in the evolution of the most massive stars (Chiosi & Maeder 1986). However, there are good reasons to expect that metal-free stars will be much less effective at driving winds than the roughly solar metallicity stars that we are familiar with in the Milky Way. Strong stellar winds are invariably radiation-driven, and at solar metallicities, the largest contribution to the radiative acceleration of the gas comes from the absorption and scattering of ultraviolet photons in the lines of the many metal atoms and ions present in the outflowing gas (Castor, Abbott, & Klein 1975). In metal-free gas, on the other hand, the only significant sources of opacity within an outflow will come from the lines of He⁺ (atomic hydrogen is typically fully ionized), and from Thomson scattering by free electrons. These provide orders of magnitude less radiative acceleration per unit luminosity than do the metal lines in a solar metallicity gas, and hence one can show that a metal-free Population III star can produce a line-driven wind only if the stellar luminosity is already very close to the Eddington limit (Kudritzki 2002).

Of course, as a Population III star evolves, it will not remain metal-free. It will start to produce carbon, nitrogen and oxygen internally once the stellar core begins to burn helium, and if the star is rotating, these elements can become well-mixed within the star (Meynet, Ekström & Maeder 2006). This will provide an additional source of opacity in the stellar atmosphere which may allow the most massive Population III stars to produce a weak CNO-driven wind (Krticka & Kubát 2009). However, the mass-loss rate will be small, and the fraction of the stellar mass that can lost in this way is unlikely to be larger than about 1%.

It is also possible that very massive Population III stars with luminosities close to the Eddington luminosity may produce eruptive, continuum-driven winds, similar to those we see coming from nearby luminous blue variables (LBVs) such as Car (Smith & Owocki 2006). However, as the cause of these LBV eruptions is not yet fully understood even for nearby objects, it is difficult to say with certainty whether they will actually be produced by Pop. III stars. More work on this topic is clearly necessary.

Finally, mechanical feedback can also be generated in the form of hydrodynamical or magnetohydrodynamical jets or outflows. We have already discussed the magnetically-driven disk winds produced in the Machida et al. (2006, 2008) simulations, which are able to eject roughly 10% of the infalling gas from the disk. Although, as we noted previously, these simulations only modelled the very earliest stages in the formation of the protostellar accretion disk, their value for the mass ejection rate is in good agreement with the predictions of a semi-analytical study of Pop. III disks and outflows carried out by Tan & Blackman (2004). If this value is correct, then it implies that the reduction in the protostellar accretion rate brought about by these outflows is small, and hence that they will not significantly limit the final stellar mass. However, one should bear in mind that their interaction with the star-forming halo on larger scales has not yet been modelled in any detail, and hence it is difficult to be certain regarding their final impact.

Radiative feedback

There are several different forms of radiative feedback that could potentially affect the accretion of gas by a Pop. III protostar. First, if the radiation is absorbed or scattered, then it will exert a force on the gas. If this force is comparable to or larger than the gravitational force acting on the gas, then it may suppress accretion onto the protostar, or even prevent it completely. Second, radiation may destroy the H₂ molecules responsible for cooling the gas. In the absence of cooling, the gas will evolve adiabatically, which again may reduce the rate at which it can be accreted. Third, the radiation may heat the gas. If radiative heating raises the gas temperature to a point at which the thermal energy of the gas exceeds the gravitational binding energy of the system, then this again will strongly suppress accretion.

In local star-forming regions, the first of these three forms of radiative feedback is believed to be the most important. Radiation pressure exerted on infalling dust grains by radiation from the protostar results in a substantial momentum transfer to the dust, and from there to the gas, since the dust and gas are strongly coupled. In spherically symmetric models, the radiative force exerted by the radiation on the dust can be strong enough to bring accretion to a complete halt (Wolfire & Cassinelli 1987). In primordial gas, there is no dust, and so this process cannot operate. However, radiation pressure can also work directly on the gas, and so it is worthwhile investigating whether this process is likely to significantly suppress accretion.

Let us start by assuming that the bolometric luminosity of the protostar is given by the Eddington luminosity Eddington luminosity

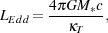(80)

where M_* is the protostellar mass, and _{T T} / m_p 0.4 cm² g^-1 is the opacity due to Thomson scattering for a fully ionized gas composed of pure hydrogen, with _T the Thomson scattering cross-section of the electron and m_p the mass of the proton. In this case, then we know from the definition of the Eddington luminosity that the radiative force exerted on a fluid element will be equal to the gravitational force exerted on it by the protostar when the opacity of the fluid element is equal to _T. More generally, we can write the ratio of the forces acting on the fluid element as

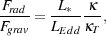(81)

where F_rad is the radiative force, F_grav is the gravitational force, L_* is the protostellar luminosity, and is the mean opacity of the fluid element. Since the protostar is unlikely to be stable if L_* > L_Edd, this implies that in order for the radiative force to significantly affect the gas, it must have a mean opacity ~ _T or higher. In practice, the luminosity of a Pop. III protostar before it reaches the main sequence will often be significantly less than the Eddington luminosity (see e.g. Smith et al. 2011), in which case an even higher mean opacity is required.

The mean opacity of metal-free gas has been computed by a number of authors, most recently by Mayer & Duschl (2005b). They present tabulated values for both the Rosseland mean opacity Rosseland mean opacity

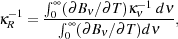(82)

and the Planck mean opacity

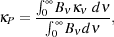(83)

where is the frequency-dependent opacity and B is the Planck function. For our purposes, we are most interested in the Planck mean. Strictly speaking, this Planck mean opacity is the same as the mean opacity in Equation 81 only if the protostar has a black-body radiation field and a photospheric temperature that is the same as the gas temperature, and in general this will not be the case. However, if the protostar is still in the pre-main sequence phase of its evolution, it will have a photospheric temperature T_p ~ 6000 K (Stahler, Palla & Salpeter 1986a) and a spectrum that does not differ too greatly from a black-body, while the temperature of the surrounding gas will typically be of the order of 1000-2000 K or higher (Clark et al. 2011b, Greif et al. 2011a, Smith et al. 2011). In these conditions, the error we make by using the Planck mean opacity in Equation 81 should not be excessively large.

There are two regimes in which the tabulated values of _p in Mayer & Duschl (2005b) exceed _T. The first occurs at very high densities (n > 10²² cm^-3), where _p > _T for a wide range of temperatures. However, these extreme densities are only reached within the protostar and hence this regime is of no relevance when we are considering feedback from the protostar on the surrounding gas. The second regime in which _p grows to the required size is at temperatures above 8000 K, for a wide range of densities. At these temperatures, the dominant source of opacity is the scattering of photons in the Lyman series lines of hydrogen, primarily Lyman-. The effects of Lyman- radiation pressure in metal-free gas were considered by Oh & Haiman (2002), in the context of the formation of massive star-forming minihalos with virial temperatures T > 10⁴ K. They argued that the Lyman- photons produced by the cooling of the hot gas would not be important (see also Rees & Ostriker 1977), but that the Lyman- photons produced by a massive star and its associated HII region would have a pronounced effect on the gas, and could significantly delay or even halt the inflow of the gas. However, they did not carry out a full quantitative investigation of the effects of Lyman- radiation pressure. More recently, this issue was revisited by McKee & Tan (2008), who studied it in some detail. They found that in a rotating flow, most of the Lyman- photons would eventually escape along the polar axis of the flow, as it is here that the optical depths are smallest. They showed that if the rotational speed of the gas were at least 10% of the Keplerian velocity, then Lyman- radiation pressure would be able to reverse the direction of the flow along the polar axis once the protostellar mass reached 20 M. The radiation would therefore blow out a polar cavity, allowing more Lyman- photons to escape. This prevents the radiation pressure from rising further, and McKee & Tan argue that it never becomes large enough to significantly affect the inflow of gas from directions far away from the polar axis (e.g. from the accretion disk). For this reason, they conclude that Lyman- radiation pressure is unlikely to be able to significantly reduce the protostellar accretion rate.

Let us now turn our attention to the second form of radiative feedback mentioned above: the photodissociation of H₂ and the consequent dramatic reduction in the cooling rate. As we have already discussed, at early times the photospheric temperature of the protostar is too low for it to produce significant quantities of far-ultraviolet radiation, and hence radiation from the protostar does not significantly affect the H₂. Once the protostar reaches the main sequence, however, it can become a significant source of far-ultraviolet radiation, provided that it has a mass greater than around 15 M (McKee & Tan 2008). Studies by Omukai & Nishi (1999) and Glover & Brand (2001) considered the effect that this radiation would have on the H₂ surrounding the protostar, and showed that the time required to photodissociate the H₂ would be significantly less than the lifetime of the protostar. The removal of the H₂ from the gas means that it is no longer able to cool effectively at temperatures T < 10⁴ K, and hence one would expect that as the H₂ in the accreting gas is destroyed, the gas will begin to evolve adiabatically until it reaches this temperature. McKee & Tan (2008) consider whether this switch to adiabatic evolution is sufficient to halt accretion, and conclude that it is not. If no protostar were present, then the switch to adiabatic evolution would be enough to stabilize the gas and prevent further collapse. The presence of the protostar, however, serves to destabilize the gas, allowing accretion to continue even when the evolution of the gas is fully adiabatic. McKee & Tan (2008) use the treatment of protostellar accretion introduced in Fatuzzo, Adams & Myers (2004) to investigate the issue numerically, and show that an increase in the effective adiabatic increase of the gas from _eff = 1.1 (which approximately characterizes the temperature evolution of the gas at n > 10⁴ cm^-3; see e.g. Omukai & Nishi 1998) to _eff = 5/3 reduces the accretion rate by only 20%.

The third possible form of radiative feedback involves the heating of the surrounding gas by radiation from the protostar. If the temperature of the gas can be increased to a point at which its thermal energy exceeds its gravitational binding energy, then it will no longer be gravitationally bound to the protostar, and hence will not be accreted. A convenient way to quantify the relative importance of thermal and gravitational energy is to compare the sound-speed of the gas with the escape velocity of the system, v_esc: gas with c_s > v_esc will not be gravitationally bound.

For an isolated protostar of mass M_*, we can write v_esc at a distance R from the protostar as:

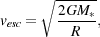(84)

where G is the gravitational constant. If we rewrite this expression in more convenient units, we find that

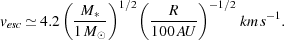(85)

For a primordial, fully molecular gas, c_s = 4.2 km s^-1 at a temperature T ~ 3400 K, and hence gas within 100 AU of a one solar mass protostar must be heated up to a temperature of thousands of Kelvin in order to unbind it. At larger distances, the required temperature would appear at first to be much smaller, but the reader should recall that this expression is for an isolated protostar, i.e. one which is not surrounded by gas. It is therefore only valid when the protostellar mass M_* is much larger than the mass of gas within a distance R of the protostar, and once we start considering scales R ≫ 100 AU, this is unlikely to be a good approximation. If we include the influence of this gas by replacing M_* in Equation 84 by M_tot = M_* + M_gas, and use the facts that prior to star formation, the mass enclosed within a sphere of radius 100 AU is roughly 5 M and increases at larger distances as M_enc R^0.8, then at distances R > 100 AU, we have

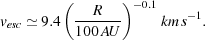(86)

In other words, once we account for the mass of the infalling gas in addition to the mass of the protostar, we find that the escape velocity is of the order of 10 km s^-1, with little dependence on the distance from the protostar. An escape velocity of this order of magnitude corresponds to a gas temperature of order 10⁴ K. This immediately tells us that heating of the gas by radiation from the protostar during the pre-main sequence phase of its evolution is unlikely to significant affect the accretion rate due to the low photospheric temperature of the protostar during this phase - clearly, a protostar with an effective temperature of 6000 K will not be able to heat up distant gas to a temperature of 10000 K. On the other hand, once the protostar reaches the main sequence, its photospheric temperature will sharply increase, and hence it may be able to heat up the surrounding gas to a much higher temperature. In particular, if the protostar is massive enough to emit a significant number of ionizing photons while on the main sequence, then it will easily be able to produce temperatures in excess of 10⁴ K within the gas that it ionizes.

The idea that the formation of an HII region may strongly suppress or completely terminate protostellar accretion was discussed long ago in the context of present-day star formation (see e.g. Larson & Starrfield 1971), but has recently been re-examined by several authors in the context of primordial star formation. On large scales (R > 0.1 pc), the behaviour of an HII region produced by a Pop. III star is relatively simple. The radial density profile of the gas on these scales is approximately R^-2.2, and hence the density falls off too quickly to trap the HII region within the minihalo (see e.g Whalen, Abel & Norman 2004, Alvarez, Bromm & Shapiro 2006, Abel, Wise & Bryan 2007, Yoshida et al. 2007). The ionization front therefore expands rapidly, as an R-type front, with a velocity that is controlled by the rate at which ionizing photons are being produced by the star. In addition, if we are considering Pop. III star formation within one of the first star-forming minihalos, then it is easy to show that sound speed of the gas within the HII region will be higher than the escape velocity of the minihalo. Consequently, the ionized gas begins to flow out of these small minihalos, significantly reducing the mean gas density. It is therefore clear that once the HII region reaches a size of 0.1 pc or above, it will act to prevent any further infall of gas from these scales onto the protostar. However, this leaves unanswered the question of how long it takes for the HII region to expand to this scale.

In the case of steady, spherically-symmetric infall, Omukai & Inutsuka (2002) showed that in order for the HII region to avoid being trapped on scales close to the protostar, the flux of ionizing photons must exceed a critical value

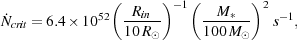(87)

where R_in is the inner radius of the HII region, which we can take to be equal to the radius of the massive star. Given reasonable values for R_in and M_*, this expression yields a value for 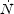_crit that is much larger than the number of photons that will actually be produced by any massive star, leading Omukai & Inutsuka (2002) to conclude that the HII region would remain trapped close to the star. However, this conclusion depends crucially on the assumed spherical symmetry of the flow. In the more realistic case in which our protostar is surrounded by an accretion disk, McKee & Tan (2008) show that the HII region can expand in all directions other than those close to the midplane of the disk once the stellar mass reaches a value of around 50-100 M, where the precise value required depends on how rapidly the gas is rotating. McKee & Tan (2008) also show that the accretion disk can survive for a considerable period after the HII region has broken out, and that the protostar will stop accreting from the disk only once the rate at which gas is lost from the disk by photoevaporation exceeds the rate at which fresh gas is falling onto the disk. In their models, this occurs for M_* ~ 140 M, leading them to conclude that radiative feedback from the protostar on the surrounding gas cannot prevent the protostellar mass from becoming very large. On the other hand, initial attempts to model this process in 2D or 3D (Hosokawa et al. 2011, Stacy, Greif & Bromm 2012) find significantly smaller final masses, M_* ~ 30-40 M, although these detailed models have so far explored only a small part of the potential parameter space.

3.2. The fragmentation model

3.2.1. Early studies

The first simulations of primordial gas to make use of sink particles were the SPH simulations of Bromm, Coppi & Larson (1999, 2002). They studied the formation of isolated dark matter minihalos and the cooling and gravitational collapse of gas within them using a somewhat idealized set of initial conditions. At an initial redshift z = 100, they created a spherical, uniform density region containing both gas and dark matter, and with an initial velocity field corresponding to the Hubble expansion. The density of this spherical region was taken to be higher than the cosmological background density, and was fixed such that the region would gravitationally collapse and virialize at a specified redshift, chosen to be z = 30 in most of the models that they examined. Small-scale structure was introduced into the dark matter distribution by perturbing the particles slightly from their initial positions using the Zel'Dovich (1970) approximation. The amplitudes of these random perturbations were fixed such that the small-scale density structure in the dark matter would begin to evolve in the non-linear regime at the virialization redshift. Both the dark matter and the gas were also assumed to be in solid body rotation, with some specified angular velocity.

Bromm, Coppi & Larson (2002) examined several different choices for the halo mass and initial angular velocity of the gas, and showed that starting from these initial conditions, the gas and dark matter would initially collapse in a similar fashion, but that the gas would subsequently form H₂, dissipate energy, and sink to the center of the minihalo. In most of the cases they studied, the gas would then form a rotationally-supported disk, with a radius of order 10 pc. This disk would then break up into clumps with masses M_cl ~ 100-1000 M, comparable to the Jeans mass in the disk. As these clumps were gravitationally unstable, Jeans mass they of course underwent gravitational collapse, and Bromm, Coppi & Larson (2002) therefore introduced sink particles to represent clumps that collapsed to densities greater than 10⁸ cm^-3 in order to avoid the timestep constraints discussed earlier, allowing the further evolution of the clumps to be studied.

Unfortunately, the fragmentation observed by bcl02 in their simulations is probably not realistic. One major problem lies in their choice of initial conditions, specifically in their use of solid-body rotation. Although the total angular momentum of the gas and dark matter in their simulations is comparable that measured for minihalos in more realistic cosmological simulations (Jang-Condell & Hernquist 2001, Davis & Natarajan 2010), their adoption of solid-body rotation leads to the gas having an incorrect radial profile for this angular momentum. This causes the collapse of the gas to be considerably more ordered than it would be in a real minihalo, leading to the formation of an over-large disk. Disks of this kind do not appear to form in simulations of small star-forming minihalos that start from more realistic cosmological initial conditions (e.g. Abel, Bryan & Norman 2002, Yoshida et al. 2006). A second major problem lies in the neglect of stellar feedback. Within the disk, the dynamical timescale is of the order of a million years, which is much longer than is needed for a massive Pop. III star to reach the main sequence. Therefore, if a massive star forms within the first clump to be produced within the disk, the radiation from this star may well be able to photodissociate the H₂ in the disk before a second clump can form (Omukai & Nishi 1999, Glover & Brand 2001).

The next attempt to use sink particles to study the formation of Pop. III stars was made by Bromm & Loeb (2004). The initial setup of their simulation was similar to that used by Bromm, Coppi & Larson (2002), but to gain improved resolution in the centre of the minihalo, they used a technique called particle splitting (Kitsionas & Whitworth 2002, Bromm & Loeb 2003). The evolution of the minihalo was followed until cold, dense gas started to build up in the centre of the halo. The simulation was then paused, and the gas within a radius of 3.1 pc of the centre of the minihalo (corresponding to roughly 3000 M of material) was resampled using SPH particles with much smaller masses, using the resampling technique described in Bromm & Loeb (2003). The mass resolution within this resampled region was thereby improved from M_res = 200 M to M_res = 4 M. Bromm & Loeb then restarted the simulation, and followed the further gravitational collapse of the gas within this central, higher resolution region until the gas density reached n ~ 10¹² cm^-3, at which point a sink particle was created. They then followed the accretion of gas onto this sink for roughly 10⁴ years, as we have already described above. Bromm & Loeb (2004) found no evidence for fragmentation within the central clump of dense gas, but did note that a second dense clump formed nearby, with a final separation from the star-forming clump of roughly 0.25 pc. However, the free-fall collapse time of this clump was about 3 Myr, and so it was unclear whether it would survive for long enough to form a second star, or whether it would be destroyed by negative feedback from a massive star forming within the first clump.

3.2.2. The importance of turbulence

Although the Bromm & Loeb (2004) study undoubtedly represented a significant step forwards in resolution compared to Bromm, Coppi & Larson (2002), it still had a mass resolution which was more than two orders of magnitude greater than the actual size of a Pop. III protostar at the moment that it forms, and hence it was unable to investigate the behaviour of the gas on scales smaller than about 100 AU. The first work using sink particles that did manage to probe this regime was Clark, Glover & Klessen (2008). Although the main focus of their study was on the fragmentation brought about by dust cooling in low metallicity systems (see e.g. Omukai et al. 2005, Schneider et al. 2006 or Dopcke et al. 2011 for more on this topic), they also studied the behaviour of the gas in the Z = 0 case for the purpose of comparing it with the results on their low metallicity runs. As the initial conditions for their simulations, Clark, Glover & Klessen (2008) considered a uniform density cloud, with a mass of 500 M, a radius of 0.17 pc and a number density of 5 × 10⁵ cm^-3. The gas within this cloud was given a low level of initial turbulence, with a turbulent energy equal to 10% of the gravitational potential energy, and was also assumed to be rotating uniformly, with an initial rotational energy equal to 2% of the gravitational potential energy. Two different simulations were performed, with different numbers of particles: a low resolution simulation that used only two million SPH particles, and hence had a mass resolution of 0.025 M, and a high resolution simulation that used 25 million particles, corresponding to a mass resolution of 2 × 10^-3 M. Aside from the somewhat artificial initial conditions, the main simplification made in these simulations was the use of a tabulated equation of state to follow the thermal evolution of the gas. The results of the Omukai et al. (2005) one-zone model were used to derive internal energy densities and thermal pressures for the gas at a range of different densities, and this data was then used to construct a look-up table that could be used by the SPH code to compute the internal energy and pressure corresponding to a given gas density.

Clark et al. followed the collapse of the gas in their simulation down to a physical scale of less than an AU (corresponding to a gas density of over 10¹⁶ cm^-3). Regions collapsing to even smaller scales were replaced by sink particles, created using the standard Bate, Bonnell & Price (1995) prescription. Clark et al. showed that at the point at which the first sink particle formed, the radial profiles of quantities such as the gas density or the specific angular momentum were very similar to those found in previous studies of Pop. III star formation that were initialized on cosmological scales (e.g. Abel, Bryan & Norman 2002, Yoshida et al. 2006). They noted that at this point in the simulation, there is no sign of any fragmentation occurring, and argued that if the simulation were stopped at this point (as would be necessary if the sink particle technique were not being used), one would probably conclude that the gas would not fragment, but would merely be accreted by the protostar. However, they show that this is not what actually happens when the simulation is continued. Instead, the gas fragments, forming 25 separate protostars after only a few hundred years. Clark et al. stopped their simulations after 19 M of gas had been incorporated into sink particles, and showed that at this point the protostars have masses ranging from 0.02 M to 5 M, but that the mass distribution is relatively flat, with most of the mass locked up in the few most massive protostars. There is no significant difference between the mass function of sinks in the low and high resolution calculations, suggesting that fragmentation is well-resolved in both cases.

This is an intriguing result, but several reasonable concerns could be raised regarding the numerical technique adopted by Clark, Glover & Klessen (2008). First, the initial conditions for the gas are an idealized version of what one would find within a real star-forming minihalo, and although there are indications that the gas loses its memory of the initial conditions prior to fragmentation occurring, inevitably a few doubts remain. Second, and more importantly, the use of a tabulated equation of state represents a major simplification of the thermal evolution of the gas, and one which may make fragmentation more likely to occur. For example, this technique does not allow one to model the formation of the hot, shocked regions noted by Turk, Norman & Abel (2010) in which much or all of the H₂ is dissociated, and it is likely to underestimate the temperature of gas falling in at later times, when the typical infall velocity is larger than during the initial assembly of the protostar. The Clark et al. calculation also neglects the effects of radiative feedback from the protostars, and assumes that protostars do not merge, even if they come within sub-AU distances of each other.

In a follow-up study, Clark et al. (2011a) addressed one of these concerns - the use of a tabulated equation of state - by performing simulations that replaced this with a detailed treatment of the chemistry and cooling of primordial gas. In their study, they investigated the role that low Mach number turbulence might play in triggering fragmentation in the gas by performing a set of simulations of the collapse of unstable Bonnor-Ebert spheres. They considered three initial configurations: a 1000 M cloud with an initial temperature of 300 K; a 150 M cloud with an initial temperature of 75 K; and a 1000 M cloud with an initial temperature of 75 K. In each case, the central density of the Bonnor-Ebert sphere was taken to be n_c = 10⁵ cm^-3. The first set of initial conditions were intended to correspond to the conditions that one would expect to find within one of the first star-forming minihalos, while the second set were intended to correspond to the conditions within a minihalo dominated by HD cooling. Simulations with the third set of initial conditions were run to allow the effects of lowering the temperature and lowering the total mass to be distinguished. Within the Bonnor-Ebert spheres, a turbulent velocity field was imposed, with a three-dimensional RMS velocity v_turb.

Clark et al. (2011a) did not claim that this was a completely accurate model of the physical state of the gas within a real star-forming minihalo. Instead, they treated this study as a kind of physics experiment, allowing them to investigate the effect of varying a single important parameter - the turbulent kinetic energy - without varying any of the other parameters in the problem, something that it would not be possible to do if using initial conditions derived from a cosmological simulation. For the first two setups described above, they performed four simulations, with v_turb = 0.1, 0.2, 0.4 and 0.8 c_s, respectively, where c_s was the initial sound speed. For the third setup (the large, low temperature clouds), they performed only two simulations, with v_turb = 0.4 and 0.8 c_s, respectively. The clouds were modelled using two million SPH particles in each case, yielding a mass resolution of 0.05 M for the 1000 M clouds and 0.0075 M for the 150 M clouds. Sink particles were created once the gas density exceeded 10¹³ cm^-3, and the sink accretion radius was 20 AU.

Clark et al. (2011a) found that fragmentation occurred in almost all of their simulated clouds. In the case of the massive, warm clouds, the only case in which fragmentation did not occur was the simulation with v_turb = 0.1 c_s. In this simulation, the gas simply collapsed to form a single, massive protostar. In the simulations with larger turbulent energies, however, the formation of the first protostar was followed within a couple of hundred years by the fragmentation of the infalling gas and the formation of a significantly larger number of protostars. The relationship between the turbulent energy and the degree of fragmentation is not straightforward: the v_turb = 0.4 c_s run fragmented more than the v_turb = 0.2 c_s, as one might expect, but the v_turb = 0.8 c_s run fragmented less than the v_turb = 0.4 c_s run (although still more than the v_turb = 0.2 c_s run). Clark et al. hypothesize that this difference in behaviour is due to the amount of angular momentum retained within the collapsing region, which in this case was larger in the v_turb = 0.4 c_s run than in the other runs, but note that this may not always be the case, and that a much larger series of realizations of the turbulent velocity field would be needed to make a definitive statement about the relationship between the turbulent energy and the degree of fragmentation (c.f. Goodwin, Whitworth, & Ward-Thompson 2004 who come to a similar conclusion regarding present-day star formation). The total amount of mass accreted by the sinks is very similar in all four runs, and hence the runs that fragment more tend to form lower mass objects than the runs that fragment less.

In the low-mass, colder clouds, Clark et al. find a much lower degree of fragmentation, despite the fact that the initial number of Jeans masses in these clouds is the same as in the 1000 M, T = 300 K clouds. In this case, fragmentation occurs only in the v_turb = 0.2 c_s and v_turb = 0.8 c_s simulations, and only a small number of fragments are formed in each case. Clark et al. investigate whether this is due to the lower cloud mass by modelling the collapse of 1000 M clouds with the same lower initial temperature, and find that although more fragmentation occurs in this case, the gas still fragments less than in the 1000 M, T = 300 K case. They suggest that this somewhat counterintuitive behaviour is due to the greater stiffness of the effective equation of state in the colder clouds. In both cases, the gas must heat up from its initial temperature at 10⁵ cm^-3 to a temperature of roughly 1000 K at 10¹⁰ cm^-3, and so when the initial temperature is lower, the gas must heat up more rapidly with increasing density, meaning that it has a larger effective adiabatic index. This makes it more difficult to generate the small-scale non-linear structures that are the seeds for later fragmentation, and also delays the collapse, allowing more of the turbulent energy to dissipate. A similar effect has previously been noted by Yoshida, Omukai & Hernquist (2007) and Tsuribe & Omukai (2008), and calls into question the common wisdom that minihalos in which the cooling becomes HD-dominated will inevitably form lower mass stars.

3.2.3. Models using cosmological initial conditions

In order to establish whether the fragmentation seen in the Clark, Glover & Klessen (2008) model was simply a consequence of the highly idealized initial conditions used in that study, several recent follow-up studies have re-examined the issue using simulations initialized on cosmological scales (i.e. scales significant larger than the virial radius of the minihalo). One of the first of these studies was carried out by Stacy, Greif & Bromm (2010). They first performed a medium resolution cosmological simulation, which allowed them to determine the formation site of the first minihalo large enough to cool effectively and form stars. They then used a hierarchical zoom-in procedure (Navarro & White 1994, Tormen, Bouchet & White 1997, Gao et al. 2005) to improve the resolution within a region centered on this formation site, allowing them to achieve a mass resolution of 1.5 M within the centre of the star-forming minihalo. ⁵ In contrast to Clark, Glover & Klessen (2008), the thermal and chemical evolution of the gas was followed in detail during the collapse. Once the gravitationally collapsing gas reached a density of 10¹² cm^-3, it was converted into a sink particle, along with all of the gas within an accretion radius r_acc = 50 AU. Stacy et al. show that following the formation of this first sink, the infalling gas collapses into a flattened disk. At a time t = 250 yr after the formation of the first sink particle, this disk has a radius of 200 AU, but it grows with time and has reached a radius of 2000 AU by t = 5000 yr, the end of the simulation. H₂ cooling allows the gas within the disk to remain at a temperature of roughly 1000 K, and the disk soon becomes gravitationally unstable, forming a second sink particle after roughly 300 yr, and a further three sinks after 4000-5000 years of evolution. At the end of the simulation, the first two sinks to form have become very massive, with masses of 43 M and 13 M respectively, while the three newer sinks still have masses ~ 1 M, close to the resolution limit of the simulation. Stacy, Greif & Bromm (2010) do not include the effects of accretion luminosity in their simulation directly, but do assess its effects during a post-processing stage. They investigate the possible effects of radiation pressure, but show that this remains unimportant within their simulation throughout the period that they simulate, in agreement with our analysis above.

The main drawback of the Stacy, Greif & Bromm (2010) study is their choice of mass resolution. At the point at which it fragments, the protostellar accretion disk in their simulation has a mass of roughly 35 M, and hence is resolved with only a few thousand SPH particles. This is two orders of magnitude smaller than the number of particles typically used to model gravitationally unstable accretion disks in the context of present-day star formation (see e.g. Rice, Lodato & Armitage 2005), and it is questionable whether a few thousand particles is enough to properly model the dynamics of the disk. It is therefore possible that the results of Stacy, Greif & Bromm (2010) may have suffered from some degree of artificial fragmentation.

More recently, a study by Clark et al. (2011b) has dramatically improved the mass resolution used to model the build-up of a protostellar accretion disk around the first Population III protostar. Clark et al. use a similar basic strategy to Stacy et al., starting with a medium resolution cosmological simulation to identify the first star-forming minihalo, and then using a hierarchical zoom-in procedure to improve the resolution within the gas forming this minihalo. They run this zoomed-in simulation until the maximum density of the gravitationally collapsing gas reaches 10⁶ cm^-3. At this point, they extract a spherical region containing 1000 M of gas from the centre of the minihalo, and resimulate this region at much higher resolution, using several nested levels of particle splitting (Kitsionas & Whitworth 2002, Bromm & Loeb 2003). At the final level of splitting, the particle mass is 10^-5 M and the mass resolution is 10^-3 M, several orders of magnitude better than in the Stacy, Greif & Bromm (2010) simulation.

In addition to the extremely high mass resolution, the other main improvement in the Clark et al. study compared to previous work is its inclusion of the effects of accretion luminosity feedback directly within the simulation. To model this, the authors start by writing the bolometric accretion luminosity produced by a given protostar as

(88)

where is the accretion rate onto that protostar, M_* is the protostellar mass, and R_* is the protostellar radius. As Clark et al. attempt to model only the first few hundred years of the evolution of the gas after the formation of the first protostar, i.e. a timescale much less than the protostellar Kelvin-Helmholtz relaxation timescale, they assume that the protostars remain in the adiabatic accretion phase of their evolution, with masses and radii that are related by Stahler, Palla & Salpeter (1986a)

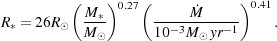(89)

The only remaining uncertainty is then , which can be directly measured within the simulation. Clark et al. next assume that the gas is heated by the accretion luminosity at a rate

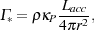(90)

where is the mass density, r is the distance to the protostar, and _p is the Planck mean opacity of the gas, calculated using the tabulated values given in Mayer & Duschl (2005b). This expression assumes that the gas is optically thin, and hence will tend to overestimate the heating rate.

Clark et al. model protostar formation using sink particles, which are created using the standard Bate, Bonnell & Price (1995) algorithm, with a density threshold n_th = 10¹⁷ cm^-3. The sink accretion radius was set to 1.5 AU. At the point at which the first sink particle forms, the state of the gas in the Clark et al. simulation (e.g. the density profile and the distribution of specific angular momentum) is very similar to that seen in other high resolution simulations of Pop. III star formation. However, the authors show that at later times, a protostellar accretion disk begins to build up around the central protostar, just as in the Stacy et al. study. The significantly higher resolution of the Clark et al. simulation allows them to model the build up of this disk on scales much closer to the central protostar, and to resolve the disk with a far larger number of SPH particles. The growth of the accretion disk is followed for around 100 years after the formation of the first protostar, and Clark et al. show that after around 90 years (corresponding to around 1.5 orbital periods for the disk), the accretion disk begins to fragment, forming several low-mass protostars. At the time at which it fragments, the disk contains several solar masses of gas (and hence is resolved with several hundred thousand SPH particles), compared to around 0.4 M in the central protostar, and the disk radius is a few tens of AU. The state of the disk at the onset of fragmentation is illustrated in Figure 4.

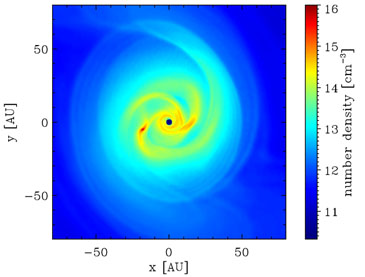Figure 4. The volume density of the protostellar accretion disk in the Clark et al. (2011a) simulation immediately prior to fragmentation. The 'hole' in the centre of the disk corresponds to the location of the sink particle representing the first protostar to form, and occurs because we have not accounted for the mass in the sink particle when calculating the density. The accretion disk is gravitationally unstable, and has formed several spiral arms, one of which has begun to fragment.

Clark et al. argue that the reason that the protostellar accretion disk fragments is that it is unable to transfer gas onto the protostar fast enough to keep up with the rate at which fresh gas is falling onto the disk. This causes the surface density of the disk to increase, which eventually results in it becoming gravitationally unstable and fragmenting. This argument can be made somewhat more quantitative if one treats the disk using the standard Shakura & Sunyaev (1973) thin disk model, and hence writes the mass flow rate through the disk at a radius r as

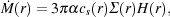(91)

where is the viscosity parameter, and c_s(r), H(r) and (r) are the sound speed, disk thickness and surface density, respectively, at a radius r. Clark et al. use the values of c_s, H and provided by their simulation to show that (r) is smaller than the accretion rate onto the disk for a wide range of radii, even if one adopts = 1 (which already presupposes that the disk is gravitationally unstable). The growth of the disk therefore appears to be unavoidable, leading to its fragmentation once portions of it develop a Toomre stability parameter Q < 1, where Q c_s / G , with here being the epicyclic frequency.

Previous semi-analytical studies of the structure of Pop. III accretion disks came to a somewhat different conclusion regarding their stability, predicting that Q ≫ 1 throughout the disk (Tan & McKee 2004, Tan & Blackman 2004, Mayer & Duschl 2005a). However, these models neglected the effect of H₂ cooling, motivated by the assumption that the H₂ content of a Pop. III protostellar accretion disk is negligible (J. Tan, private communication). This assumption leaves H^- as the primary source of opacity at temperatures T ~ 7000 K and below (Lenzuni, Chernoff & Salpeter 1991, Mayer & Duschl 2005b). For gas in chemical equilibrium, the opacity of H^- decreases sharply with decreasing temperature, and consequently these models find the equilibrium temperature of the accretion disk to be high, T ~ 6000 K. In comparison, Clark et al. show that when the effects of H₂ are taken into account, the characteristic temperature of the gas in the disk lies in the range of 1500 to 2000 K. The disks in these previous semi-analytical models could therefore transfer mass onto the protostar more rapidly than the disk in the Clark et al. simulation, owing to their higher sound-speed and larger thickness, but at the same time were also more stable against gravitational fragmentation. It is therefore not surprising that these previous studies predicted that the accretion disk should be stable, and highlights the crucial role played by H₂ cooling in enabling disk fragmentation.

In addition to the simulation described above, in which the value of used to calculate the accretion luminosity was measured directly, Clark et al. also performed two additional simulations in which was kept fixed, allowing them to investigate the role played by accretion luminosity heating. They considered cases with = 10^-3 M yr^-1 (somewhat smaller than the measured value) and = 10^-2 M yr^-1 (larger than the measured value), and showed that as (and hence L_acc) increase, the disk becomes warmer and thicker and takes longer to fragment. However, fragmentation still occurs in every case, demonstrating that accretion luminosity heating is unable to prevent the disk from fragmenting (c.f. Krumholz 2006 who argues that it plays a crucial role in suppressing fragmentation in local star-forming systems).

One drawback of the Clark et al. (2011b) study is that they examined only a single star-forming minihalo, and although they showed that the properties of this halo (e.g. mass, spin parameter, formation redshift) were similar to those of the minihalos modelled in previous studies of Pop. III star formation, nevertheless the suspicion remains that perhaps this particular minihalo was unusual in some way. This concern was addressed by Greif et al. (2011a). They used the new moving-mesh code AREPO (Springel 2010) to study Pop. III star formation in five different minihalos, using a sink particle algorithm to allow them to follow the evolution of the gas past the point at which the first protostar formed. In all five of the systems that they modelled, they found similar behaviour to that in the Clark et al. study: an accretion disk built up around the first protostar, became gravitationally unstable, and began to fragment after only a few years. These results suggest that Clark et al. were right to claim that disk fragmentation, and the resulting formation of Pop. III binary systems, or higher order multiple systems, is an almost inevitable outcome of Population III star formation.

Greif et al. (2011a) also examined the issue of whether the objects represented by the individual sink particles would truly survive as separate protostars, or whether they would simply merge into a single massive protostar as the system evolved further. They considered two different schemes for merging sink particles. In the standard scheme, sink particles coming within a distance of 100 R of each other were merged to form a single sink, provided that the total energy of the two-body system was negative. In an alternative model, utilizing what Greif et al. dub as "adhesive" sinks, the energy check was omitted, and sinks were always merged when within a distance of 100 R of each other. Greif et al. justify their choice of this critical distance in two ways: first, it is also the accretion radius adopted for their sinks, meaning that the gas flow on smaller scales close to the sinks is not resolved; and second, it is roughly equal to the maximum size of a pre-main sequence protostar predicted by the models discussed in Section 3.1.2.

The majority of the protostars formed in the Greif et al. simulations have at least one close encounter with another protostar, but when the standard merger algorithm is used, many of these encounters result in a purely dynamical interaction, as the total energy of the protostellar pair is too large to allow them to merge. On the other hand, when the adhesive sinks are used, many of these encounters lead to mergers. Greif et al. show that although the total mass incorporated into protostars is roughly the same in both cases, the number of protostars that survive as individual objects is reduced by a factor of up to a few, and the mean protostellar mass is consequently higher. In both cases, the protostars have a relatively flat mass distribution, with most of the protostellar mass being accounted for by a small number of high-mass protostars. The protostars have a broad distribution of radial velocities, ranging from v_rad ~ 1 km s^-1 to v_rad ~ 100 km s^-1, and in many cases the radial velocity is greater than the escape velocity of the central region of the minihalo. It is likely that this leads to a significant fraction of the Pop. III protostars escaping from the minihalo entirely, although Greif et al. do not follow their evolution for long enough to confirm this. It is possible that these protostars will accrete very little additional gas once they escape from the high density region at the centre of the minihalo (see e.g. Johnson & Khochfar 2011), in which case their final masses would be very similar to the masses that they have at the point at which they are ejected. Greif et al. show that in the standard case, a considerable number of these ejected protostars have masses M < 1 M. If these protostars do indeed avoid accreting further gas after their ejection, then they would have lifetimes that are comparable to the current age of the Universe. This suggests that it may be possible for some Population III stars to survive until the present day. However, when the adhesive sinks are used, the number of ejected protostars with subsolar masses is greatly reduced, demonstrating that this conclusion is highly sensitive to our treatment of protostellar mergers.

The majority of the Greif et al. simulations did not include the effects of the accretion luminosity generated by the collection of protostars. However, they did consider one case in which this was included, using the Clark et al. treatment with a fixed value for the accretion rate used in the determination of the accretion luminosity, = 0.1 M yr^-1. The effect of this was to puff up the disk, causing fragmentation to occur at a slightly larger distance from the initial protostar. However, despite the unrealistically high value adopted for , fragmentation still occurred and the number of protostars that formed was barely affected.

A more detailed study of the effects of accretion luminosity heating was carried out by Smith et al. (2011). They used Gadget to resimulate the central 2 pc of the minihalos simulated by Greif et al. (2011a), starting at a time prior to protostar formation at which the peak density of the gas was around 10⁹ cm^-3. Smith et al. (2011) evolved these systems past the time at which the first protostar formed, and used sink particles with large accretion radii (r_acc = 20 AU) to allow them to follow the dynamical evolution of the system for an extended period. For each of the five minihalos, they performed simulations both with and without accretion luminosity heating. When the accretion luminosity heating was included, it was treated in the same fashion as in Clark et al. (2011b). They found that in general, the effect of the accretion luminosity heating was to delay fragmentation and reduce the number of fragments formed. However, they also showed that the effect was relatively small, and had less influence on the number of fragments formed than did the intrinsic variation in halo properties arising from their different assembly histories. feedback!radiative|) accretion disk|)

3.2.4. Open questions

As the discussion in the previous section has shown, the past couple of years has seen a large increase in the number of simulations of Pop. III star formation that show evidence for fragmentation, suggesting that the older picture that had Pop. III stars forming in isolation with masses of 100 M or more is in need of some revision. However, many aspects of the fragmentation scenario remain unclear. Some of the most important open questions are summarized below.

• Are our treatments of optically thick H₂ cooling and accretion luminosity heating adequate?

The fragmentation of the gas observed in these simulations typically occurs at densities at which H₂ line cooling is optically thick, and hence may depend on the method used to account for the reduction that this causes in the cooling rate. At present, both of the methods in common usage represent relatively crude approximations, and it remains to be seen whether the behaviour of the gas will remain the same if a more accurate treatment is used. Similarly, the method currently used to treat the effects of accretion luminosity heating also makes a number of major simplifications that may influence the outcome of the simulations. molecular hydrogen!cooling|) feedback!radiative|)

• What role do magnetic fields play?

If a non-negligible magnetic field can be generated by the turbulent dynamo during the gravitational collapse of the gas, as discussed in Section 2.3, then this may influence the evolution and stability of the disk. The presence of a magnetic field may make the disk unstable via the magnetorotational instability (Tan & Blackman 2004, Silk & Langer 2006), although the resulting mass transfer onto the protostar is unlikely to be fast enough to prevent the disk from becoming gravitationally unstable. A more important effect may be magnetic braking of the infalling gas, which could act to significantly reduce the angular momentum of the gas reaching the disk (see e.g. Hennebelle & Ciardi 2009). Whether either of these effects can significantly suppress fragmentation remains to be determined.

• How often do Population III protostars merge?

Current simulations either ignore mergers entirely (e.g. Clark et al. 2011b, Smith et al. 2011), or treat them using very simple approximations that do not properly account for the effects of tidal forces (e.g. Greif et al. 2011a). However, it is clear from the results of the Greif et al. study that the method used to treat mergers has a significant influence on the number of protostars that survive, their mass distribution and their kinematics. Improving the accuracy with which protostellar mergers are treated within this kind of simulation is therefore an important priority.

• Can we find some way to do without sink particles?

The concerns outlined above regarding the way in which protostellar mergers are treated would be greatly ameliorated if we were able to run the simulations without sink particles, as in this case we would be able to model directly how the gas behaves on scales of the order of 100 R. To do this, however, it will be necessary to devise some scheme for treating these very small scales that does not fall foul of the Courant time constraint discussed previously. Greif et al. (2012) have recently published the results of an initial effort along these lines, but were only able to simulate the first ten years of the evolution of the disk, owing the extremely high computational cost of the calculation.

• How rapidly does H₂ photodissociation occur?

Fragmentation is dependent on the cooling provided by H₂ and does not occur in models of protostellar accretion disks that omit this effect (Tan & McKee 2004, Mayer & Duschl 2005a). It is therefore highly probable that fragmentation will cease once the H₂ has been photodissociated by Lyman-Werner band photons emitted from any massive protostars that form. What is not yet clear is how quickly this will occur. McKee & Tan (2008) show that the number of Lyman-Werner band photons produced by a zero-age main sequence Population III star increases sharply with increasing stellar mass, before levelling off at a value S_lw ~ 10⁴⁹ photons s^-1 for M_* ~ 30 M. If we assume that all of these photons are absorbed by H₂ and that 20% of these absorptions lead to dissociation (Draine & Bertoldi 1996), then the radiation from the star will photodissociate H₂ at a rate _dis = 0.1 M yr^-1, leading to complete removal of the H₂ within only a few hundred years. However, it is likely that many of the available photons will not be absorbed by H₂, either because they never coincide with one of the Lyman-Werner band lines, or because they escape along a direction in which most of the H₂ has already been dissociated, or because they are absorbed by atomic hydrogen (Glover & Brand 2001), and so the dissociation time for the H₂ could be significantly longer than suggested by this simple estimate, particularly once one accounts for the effects of three-body H₂ formation.

• How rapidly is the gas ionized? Does this completely suppress accretion, or simply suppress fragmentation?

As we have already discussed in Section 3.1.3, the most plausible mechanism for shutting off the supply of cold gas at the centre of the minihalo is the formation of an HII region whose thermal pressure is sufficient to expel most of the gas. However, only a few studies have looked at the interaction between the growth of the HII region and the evolution of the protostellar accretion disk. In particular, the issue has not yet been looked at within the context of the fragmentation model discussed above. It is therefore unclear how rapidly the HII region will grow, and whether it will immediately act to shut off accretion, or whether pockets of dense, cold gas can survive within the HII region for an extended period.

• Do any low-mass Population III stars survive until the present day?

One of the most exciting results of the Greif et al. (2011a) model is that some of the protostars that are ejected from the centre of the star-forming minihalo have masses that are below 0.8 M, and hence lifetimes that are longer than the current age of the Universe. If these protostars avoided accreting any further gas, then they could have survived until the present-day, raising the possibility of directly detecting truly metal-free stars within the Milky Way. However, as we have already discussed above, the number of protostars with sub-solar masses that are ejected from the star-forming region is very sensitive to the way in which protostellar mergers are treated, and hence is highly uncertain at present. In addition, it is possible that any Pop. III protostars that have survived until the present day have also become too polluted with metals by ongoing accretion from the ISM for us to recognize them as metal-free stars, although the best current estimates (Frebel, Johnson & Bromm 2009, Johnson & Khochfar 2011) suggest that the effects of pollution will be very small.

⁵ The value quoted here for the mass resolution of the Stacy, Greif & Bromm (2010) simulation assumes that 100 or more SPH particles are required to resolve gravitationally bound structures, which is the typical resolution limit adopted in studies of present-day star formation. Stacy, Greif & Bromm (2010) assume that only 48 SPH particles are required, and hence quote a mass resolution that is roughly a factor of two smaller. Back.