


Monte Carlo simulations have the advantage (and the danger) that they
are easy to do and additional distributions and constraints can be
included in the modelling. Fig. 5 shows the
results of 107 Monte Carlo simulations of SSP models with
ages following a power-law distribution between 40 Myr and 2.8 Gyr, and
 distributed following a
(discrete) power-law distribution in the range between 2 and
106 stars. The figure also shows the standard modelling
result using the mean value of the corresponding observable in the age
range from 40 Myr to 10 Gyr.
distributed following a
(discrete) power-law distribution in the range between 2 and
106 stars. The figure also shows the standard modelling
result using the mean value of the corresponding observable in the age
range from 40 Myr to 10 Gyr.
The first impression obtained from the plot is psychologically
depressing. We had developed population synthesis codes to draw
inferences from observational data, and the Monte Carlo simulations show
so large a scatter that we wonder if our inferences are correct.
Fig. 6, from
Popescu et al. (2012),
compares the age inferences for LMC clusters using Monte Carlo
simulations to sample the PDF of integrated luminosities and traditional
 2 fitting to the
mean value of the PDF (traditional
synthesis model results). The figure shows a systematic discrepancy at
young ages. Such an effect was also found by
Fouesneau et
al. (2012)
for M83 stellar clusters and by
Fouesneau and
Lançon (2010),
Silva-Villa and Larsen
(2011)
(among others) when trying to recover the inputs of the Monte Carlo
simulations using
2 fitting to the
mean value of the PDF (traditional
synthesis model results). The figure shows a systematic discrepancy at
young ages. Such an effect was also found by
Fouesneau et
al. (2012)
for M83 stellar clusters and by
Fouesneau and
Lançon (2010),
Silva-Villa and Larsen
(2011)
(among others) when trying to recover the inputs of the Monte Carlo
simulations using
 2 fitting to the
mean value obtained by parametric
models. This requires stepwise interpretation. First, we must understand
Monte Carlo simulation results. Second, we must figure out how to use
Monte Carlo simulations to make inferences about observational data
(hypothesis testing).
2 fitting to the
mean value obtained by parametric
models. This requires stepwise interpretation. First, we must understand
Monte Carlo simulation results. Second, we must figure out how to use
Monte Carlo simulations to make inferences about observational data
(hypothesis testing).
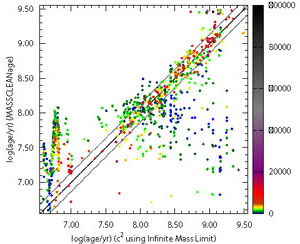 |
Figure 6. MASSCLEAN age
(Popescu and
Hanson 2010b)
results versus a
|
4.1. Understanding Monte Carlo simulations: the revenge of the stellar luminosity function
The usual first step is to analyse (qualitatively) the results for Monte
Carlo simulations that implicitly represent how

 (L1, ...,Ln;
tmod) varies with
(L1, ...,Ln;
tmod) varies with
 (Bruzual 2002,
Cerviño and
Valls-Gabaud 2003,
Popescu and Hanson
2009,
2010a,
b,
Piskunov et
al. 2011,
Fouesneau and
Lançon 2010,
Silva-Villa and Larsen
2011,
da Silva et al. 2012,
Eldridge 2012).
In general, researchers have found that at very low
(Bruzual 2002,
Cerviño and
Valls-Gabaud 2003,
Popescu and Hanson
2009,
2010a,
b,
Piskunov et
al. 2011,
Fouesneau and
Lançon 2010,
Silva-Villa and Larsen
2011,
da Silva et al. 2012,
Eldridge 2012).
In general, researchers have found that at very low
 values, most simulations
are situated in a region away from the mean obtained by parametric
models; at intermediate
values, most simulations
are situated in a region away from the mean obtained by parametric
models; at intermediate
 values, the distribution
of integrated luminosities or colours are (sometimes) bimodal ; at large
values, the distribution
of integrated luminosities or colours are (sometimes) bimodal ; at large
 values, the distributions
become Gaussian.
values, the distributions
become Gaussian.
The different situations are shown quantitatively in
Fig. 7, taken from
Cerviño (2003),
which can be
fully understood if we take advantage of the Monte Carlo simulations and
the parametric description of synthesis models (after
Gilfanov et al. 2004,
Cerviño and
Luridiana 2006).
For ages greater than 0.1 Gyr, the figure compares when the mean
bolometric luminosity of a cluster with
 stars,
Lbolclus =
stars,
Lbolclus =
 ×
µ1'(ℓbol;
tmod), equals the maximum value of
×
µ1'(ℓbol;
tmod), equals the maximum value of
 (ℓbol; tmod),
L*,bolmax. This can be interpreted as the
situation in which the light of a cluster is dominated by a single star,
called the `lowest luminosity limit' by
Cerviño and
Luridiana (2004).
In addition, the
(ℓbol; tmod),
L*,bolmax. This can be interpreted as the
situation in which the light of a cluster is dominated by a single star,
called the `lowest luminosity limit' by
Cerviño and
Luridiana (2004).
In addition, the  value
needed to have, on average, at least 1 PMS star is also computed; it can
be obtained using a binomial distribution over the IMF for stars below
and above mTO. The corresponding
value
needed to have, on average, at least 1 PMS star is also computed; it can
be obtained using a binomial distribution over the IMF for stars below
and above mTO. The corresponding
 values are expressed as
the mean total mass of the cluster,
values are expressed as
the mean total mass of the cluster,
 .
.
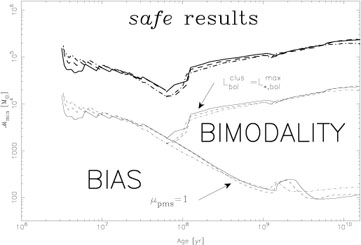 |
Figure 7.
|
From the description of
 (ℓtmod) we know that the
distribution is
L-shaped with a modal value (maximum of the distribution) in the MS
region and a mean located somewhere between the MS and PMS regions. The
mean number of PMS will be less than one at low
(ℓtmod) we know that the
distribution is
L-shaped with a modal value (maximum of the distribution) in the MS
region and a mean located somewhere between the MS and PMS regions. The
mean number of PMS will be less than one at low
 values. This means that
most simulations are low-luminosity clusters composed of only MS stars,
and a few simulations are high-luminosity clusters dominated by PMS
stars. Here, the mode of
values. This means that
most simulations are low-luminosity clusters composed of only MS stars,
and a few simulations are high-luminosity clusters dominated by PMS
stars. Here, the mode of

 (L;
tmod) is defined by MS stars and is biased with
respect to the mean of
(L;
tmod) is defined by MS stars and is biased with
respect to the mean of

 (L;
tmod). We can also be sure that the distribution
(L;
tmod). We can also be sure that the distribution

 (L;
tmod) is not Gaussian-like if its mean is lower than
the maximum of
(L;
tmod) is not Gaussian-like if its mean is lower than
the maximum of
 (ℓ
;tmod), since the shape of the
distribution is sensitive to how many luminous stars are present in each
simulation (e.g. 0, 1, 2, ...) and this leads to bumps (and possibly
multi-modality) in
(ℓ
;tmod), since the shape of the
distribution is sensitive to how many luminous stars are present in each
simulation (e.g. 0, 1, 2, ...) and this leads to bumps (and possibly
multi-modality) in

 (L;
tmod). Finally, when
(L;
tmod). Finally, when
 is large,
is large,

 (L;
tmod) becomes Gaussian-like and the mean and mode
coincide.
Cerviño (2003),
Cerviño and
Luridiana (2004)
established the maximum of
(L;
tmod) becomes Gaussian-like and the mean and mode
coincide.
Cerviño (2003),
Cerviño and
Luridiana (2004)
established the maximum of
 (ℓ
;tmod) 10 times to reach this safe
result. Curiously, the value of
(ℓ
;tmod) 10 times to reach this safe
result. Curiously, the value of
 that can be inferred from
Fig. 7 can be used in combination with
that can be inferred from
Fig. 7 can be used in combination with
 1 and
1 and  2 values from
Fig. 3. The resulting
2 values from
Fig. 3. The resulting
 1:
1: and
and
 2;
2; values
are approximately 0.1, the values required for Gaussian-like
distributions obtained by the parametric analysis of the stellar
luminosity distribution function.
values
are approximately 0.1, the values required for Gaussian-like
distributions obtained by the parametric analysis of the stellar
luminosity distribution function.
This exercise shows that interpretation of Monte Carlo simulations can
be established quantitatively when the parametric description is
also taken into account. Surprisingly, however, except for Monte Carlo
simulations used to obtain SBFs
(Brocato et
al. 1999,
Raimondo et al. 2005,
González et
al. 2004),
most studies do not obtain the mean or compare it with the result
obtained by parametric modelling. Usually, Monte Carlo studies only
verify that for large
 values, using relative
values, the results coincide with standard models. In addition, hardly
any Monte Carlo studies make explicit reference to the stellar
luminosity function, nor do they compute simulations for the extreme
case of
values, using relative
values, the results coincide with standard models. In addition, hardly
any Monte Carlo studies make explicit reference to the stellar
luminosity function, nor do they compute simulations for the extreme
case of
 = 1. Thus, psychological
bias is implicit for interpretation of
= 1. Thus, psychological
bias is implicit for interpretation of
 (m0,
t, Z) referring only to stellar clusters and
synthesis models referring only to integrated properties.
(m0,
t, Z) referring only to stellar clusters and
synthesis models referring only to integrated properties.
Another application of the stellar luminosity function is definition of
the location of simulations/observations in colour-colour diagrams
(actually in any diagnostic diagram using indices that do not depend on
 ). Any integrated colour is
a combination of the contributions of different stars; hence, individual
stars define an envelope of possible colours of
simulations/observations. The situation is illustrated in
Fig. 8 taken from
Barker et al. (2008),
where the possible range of colours of individual stars and the mean of
parametric synthesis models are compared.
). Any integrated colour is
a combination of the contributions of different stars; hence, individual
stars define an envelope of possible colours of
simulations/observations. The situation is illustrated in
Fig. 8 taken from
Barker et al. (2008),
where the possible range of colours of individual stars and the mean of
parametric synthesis models are compared.
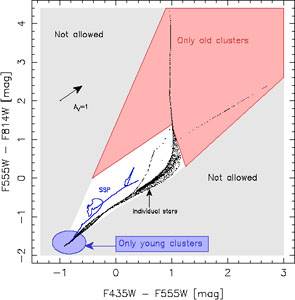 |
Figure 8. Graphical representation of the boundary conditions. The blue track shows the mean value obtained by SSP models (from the bottom-left corner of the figure to the red colour as a function of increasing age). The red area defines the region within which only old (≥ 108 yr) clusters can reside; similarly, the blue area is the region for young (≤ 5 Myr-old) clusters. The black dots show the positions of individual stars. The grey shaded areas cannot host any clusters since there is no possible combination of single stars that can produce such cluster colours. The extinction vector for AV = 1 mag is shown for reference. Figure from Barker et al. (2008). |
The final application of parametric descriptions of the integrated
luminosity function to Monte Carlo simulations is a back-of-the-envelope
estimation of how many Monte Carlo simulations are needed for reliable
results. This number depends on the simulation objective, but a minimal
requirement is that, for a fixed
 , the mean value obtained
from the simulations (the sample mean
<
, the mean value obtained
from the simulations (the sample mean
< 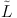 >)
must be
consistent to within an error of є of the mean obtained by the
parametric modelling (the population mean). Statistics textbooks show
that, independent of the shape of the distribution, the sampling mean is
distributed according to a sampling distribution with variance equal to
the variance of the population distribution variance divided by the
sample size:
>)
must be
consistent to within an error of є of the mean obtained by the
parametric modelling (the population mean). Statistics textbooks show
that, independent of the shape of the distribution, the sampling mean is
distributed according to a sampling distribution with variance equal to
the variance of the population distribution variance divided by the
sample size:
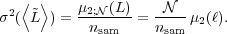 |
(8) |
Hence, expressed in relative terms, we can require that
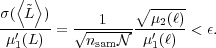 |
(9) |
We can impose a similar requirement for the variance obtained from the distribution, which results in
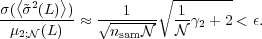 |
(10) |
An interesting result is that, for relative dispersion, the relevant
parameter is the total number of stars Ntot used in
the overall simulation set. Hence, the number of simulations needed to
sample the distribution of integrated luminosities decreases when
 increases. However, for
absolutes values, the ratio of
increases. However, for
absolutes values, the ratio of
 to nsam
is the relevant quantity.
to nsam
is the relevant quantity.
4.2. What we can learn from Monte Carlo simulations?
The principal advantage of Monte Carlo simulations is that they allow us to include constraints that are difficult to manage with a parametric description. Examples are constraints in the inputs (e.g. considering only simulations with a given number of stars in a given (observed) mass range, Knödlseder et al. 2002) or constraints in the outputs (e.g. considering only simulations that verify certain observational constraints in luminosities, Luridiana et al. 2003). The issue here is to compute Monte Carlo simulations and only consider those that are consistent with the desired constraints. Note that once a constraint is included, the process requires transformation of the associated probability distributions and hence a change in the parameters of the distribution, and some constraints cannot be expressed analytically as a function of input parameters. Another application that can easily be performed with Monte Carlo simulations is testing of hypotheses by comparing the distribution of the simulations and observations; examples have been described by Fumagalli et al. (2011), Eldridge (2012). Hence, this approach is ideal when fine-tuned to observational (or theoretical) constraints.
However, at the beginning of this section I stated that one of the
dangers of Monte Carlo simulations is that they are easy to do. They are
so easy that we can include additional distributions, such as the
distribution of numbers of stars in clusters, the total mass
distribution, an age distributions, without a fine-tuned specific
purpose. Here, the danger is that we must understand the questions that
we are addressing and how such additional distributions affect the
possible inferences. For instance,
Yoon et al. (2006)
used Monte Carlo simulations with the typical number of stars in a
globular cluster to explain bimodal distributions in globular
clusters. They argued that bimodality is the result of a non-linear
relation between metallicity and colour transformation. The
transformation undoubtedly has an effect on the bimodality; however, the
number of stars used (actually the typical number of stars that globular
clusters have) is responsible for the bimodal distributions. Monte Carlo
simulations using large
 values must converge to a
Gaussian distribution.
values must converge to a
Gaussian distribution.
When Monte Carlo simulations are used to obtain parameters for stellar
clusters, the usual approach is to apply large grids covering the
parameter space for
 and age. However, the
situation is not as simple as expected. First, a typical situation is to
use a distribution of total masses. Hence,
and age. However, the
situation is not as simple as expected. First, a typical situation is to
use a distribution of total masses. Hence,
 is described by an unknown
distribution. Even worse,
is described by an unknown
distribution. Even worse,
 fluctuates since the
simulations must include the constraint that
fluctuates since the
simulations must include the constraint that
 is an integer. Therefore,
the mean values of such simulations diverge from the mean values
obtained in the parametric description noted before, since they include
additional distributions. Second, the inferences depend on the input
distributions. For instance,
Popescu et al. (2012)
produced a grid assuming a flat distribution for total mass and a flat
distribution in logt. They compared observational colours with
the Monte Carlo grid results and obtained a distribution of the
parameters (age and mass) of the Monte Carlo simulations compatible with
the observations. When expressed in probabilistic terms, the grid of
Monte Carlo simulations represents the probability that a cluster has a
given luminosity set for given age and mass,
is an integer. Therefore,
the mean values of such simulations diverge from the mean values
obtained in the parametric description noted before, since they include
additional distributions. Second, the inferences depend on the input
distributions. For instance,
Popescu et al. (2012)
produced a grid assuming a flat distribution for total mass and a flat
distribution in logt. They compared observational colours with
the Monte Carlo grid results and obtained a distribution of the
parameters (age and mass) of the Monte Carlo simulations compatible with
the observations. When expressed in probabilistic terms, the grid of
Monte Carlo simulations represents the probability that a cluster has a
given luminosity set for given age and mass,
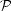 (L | t,
(L | t,
 ), and comparison of
observational data with such a set represents the probability that a
cluster has a given age and mass for a given luminosity set
), and comparison of
observational data with such a set represents the probability that a
cluster has a given age and mass for a given luminosity set
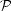 (t,
(t,
 | L). The method
seems to be correct, but it is a typical fallacy of conditional
probabilities: it would be correct only if the resulting distribution of
ages were flat in logt and if the distribution of masses were
flat. The set of simulations has a prior hypothesis about the
distribution of masses and ages, and the results are valid only so far
as the prior is realistic. In fact,
Popescu et al. (2012)
obtained a distribution of ages and total masses that differs from the
input distributions used in the Monte Carlo simulation set.
| L). The method
seems to be correct, but it is a typical fallacy of conditional
probabilities: it would be correct only if the resulting distribution of
ages were flat in logt and if the distribution of masses were
flat. The set of simulations has a prior hypothesis about the
distribution of masses and ages, and the results are valid only so far
as the prior is realistic. In fact,
Popescu et al. (2012)
obtained a distribution of ages and total masses that differs from the
input distributions used in the Monte Carlo simulation set.
The situation was also illustrated by
Fouesneau et
al. (2012),
who computed a Monte Carlo set with a flat distribution in both
logt and
log as priors. The authors
were aware of the Bayes theorem, which connects conditional
probabilities:
as priors. The authors
were aware of the Bayes theorem, which connects conditional
probabilities:
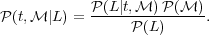 |
(11) |
They obtained age and mass distributions for observed clusters using a similar methodology to that of Popescu et al. (2012). In fact, they found that the distribution of total masses follows a power law with an exponent -2; hence, the distribution used as a prior is false. However, they claimed that the real distribution of total masses is the one obtained, similar to Popescu et al. (2012). Unfortunately, the authors were unaware that such a claim is valid only as long as a cross-validation is performed. This should involve repetition of the Monte Carlo simulations with a total mass distribution following an exponent of -2 and verification that the resulting distribution is compatible with such a prior (Tarantola 2006).
Apart from problems in using the Bayes theorem to make false hypotheses, both studies can be considered as major milestones in the inference of stellar populations using Monte Carlo modelling. Their age and total mass inferences are more realistic since they consider intrinsic stochasticity in the modelling, which is undoubtedly better than not considering stochasticity at all. The studies lack only the final step of cross-validation to obtain robust results.
Monte Carlo simulations provide two important lessons in the modelling of stellar populations that also occur in the Gaussian regime and can apply to systems of any size. The first is the problem of priors and cross-validation (i.e. an iteration of the results). The second and more important lesson is that there are no unique solutions; the best solution is actually the distribution of possible solutions. In fact, we can take advantage of the distribution of possible solutions to obtain further results (Fouesneau et al. 2012).