


We have seen the implications of probabilistic modelling for a
low- regime when Monte
Carlo simulations (or covolution of the stellar luminosity function) are
required. However, we have shown that some characteristics of
stochasticity are present independently of
regime when Monte
Carlo simulations (or covolution of the stellar luminosity function) are
required. However, we have shown that some characteristics of
stochasticity are present independently of
 (as in SBFs and partial
correlations). In addition, we have seen that we can combine different
probability distributions to describe new situations, as for integrated
luminosities at a given
(as in SBFs and partial
correlations). In addition, we have seen that we can combine different
probability distributions to describe new situations, as for integrated
luminosities at a given
 or integrated luminosities
of clusters that follow a
or integrated luminosities
of clusters that follow a
 or age distribution. Let
us explore the implications of such results.
or age distribution. Let
us explore the implications of such results.
The first implication of the modelling of stellar populations is that the redder the wavelength, the greater is the scatter, since fewer stars contribute to red wavelengths than to blue wavelengths in absolute and relative terms. In fact, each wavelength can fluctuate around the mean of the corresponding distribution of integrated luminosities in a different way, even though it is correlated with the other wavelengths. This naturally implies that for each age and metallicity, each model has its own fitting metrics.
We can take advantage of Neff or SBF definitions to
theoretically define the weight for each wavelength in a
 2 fit. In fact, a
good
2 fit. In fact, a
good  2 fit cannot
be better than the physical dispersion of
the model, which is a physical limit. Exceedance of this physical limit
(overfitting) leads to a more precise but erroneous result.
Fig. 9, taken from
Cerviño and
Luridiana (2009),
illustrates the physical dispersion used to identify overfitting for SBFs.
2 fit cannot
be better than the physical dispersion of
the model, which is a physical limit. Exceedance of this physical limit
(overfitting) leads to a more precise but erroneous result.
Fig. 9, taken from
Cerviño and
Luridiana (2009),
illustrates the physical dispersion used to identify overfitting for SBFs.
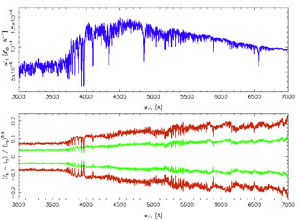 |
Figure 9. Top: Integrated mean spectra of a
1-Gyr-old cluster. Bottom: 1 and
2 |
An additional advantage of including the physical weight in the fit is
that it breaks degeneracies that are present when observational data are
fitted only to the mean value for parametric models. For instance,
Fig. 10, taken from
Buzzoni (2005),
illustrates breaking of age-metallicity degeneracy using
Neff. Given that the allowed scatter depends on age
and metallicity, the resulting
 2 defines the
probability that a fit will produce different results.
2 defines the
probability that a fit will produce different results.
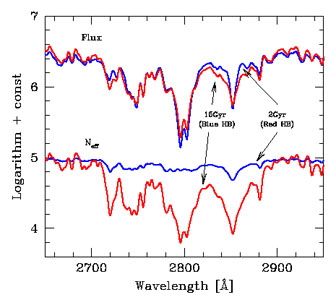 |
Figure 10. Theoretical spectral energy distribution (upper plots) and effective stellar contributors (Neff) (lower plots) for two SSPs from population synthesis models described by Buzzoni (1989, 1993) in the spectral region of the MgII and MgI features around 2800 Å. The models refer to a 2-Gyr SSP with red HB morphology and a 15-Gyr population with blue HB, as labelled. In spite of the close similarity of the spectra, the two SSPs display a large difference in terms of Neff, and hence there is much greater statistical scatter in the spectral features expected for the older SSP. Figure from Buzzoni (2005). |
Unfortunately, implementation of these ideas is not straightforward. Use
of Neff directly provides the theoretical weight for a
wavelength in a  2
fit, but it is dependent on
2
fit, but it is dependent on
 . The use of SBF is
independent of
. The use of SBF is
independent of
 . However, it cannot be
implemented directly, but requires an iterative process involving a
standard fit, use of the SBF to identify overfitted results, and
iteration of the process until convergence.
. However, it cannot be
implemented directly, but requires an iterative process involving a
standard fit, use of the SBF to identify overfitted results, and
iteration of the process until convergence.
An unexplored area involves taking full advantage of
 (Li, Lj),
which can be obtained theoretically. In fact, the covariance
coefficients and variance define a covariance matrix that can be
directly implemented in a
(Li, Lj),
which can be obtained theoretically. In fact, the covariance
coefficients and variance define a covariance matrix that can be
directly implemented in a
 2 fit. However,
as far as I know, computation of
2 fit. However,
as far as I know, computation of
 (Li, Lj) has not
been implemented and is not considered in any synthesis code (exceptions are
Cerviño et
al. 2001,
Cerviño et
al. 2002,
Cerviño and
Valls-Gabaud 2003,
González et
al. 2004)
but they use a Poisson approximation of the stellar luminosity function
and the covariance coefficients obtained are not correct).
(Li, Lj) has not
been implemented and is not considered in any synthesis code (exceptions are
Cerviño et
al. 2001,
Cerviño et
al. 2002,
Cerviño and
Valls-Gabaud 2003,
González et
al. 2004)
but they use a Poisson approximation of the stellar luminosity function
and the covariance coefficients obtained are not correct).
5.2. The population and the sample definition
The second implication is related to the definition of the population
described by computed distributions. We have seen that we can define
populations composed of  =
1 stars, which are CMD diagrams, and that we can analyse such
populations as long as we have enough events nsam to
describe the distribution.
=
1 stars, which are CMD diagrams, and that we can analyse such
populations as long as we have enough events nsam to
describe the distribution.
We can also define populations composed of events with a similar number
of stars,  , taking
advantage of additional information about the
source. For instance, we can take the luminosity profile of a galaxy. We
can assume that for a given radius, the number of stars is roughly the
same (additional information in the form of the geometry of the galaxy
is required). Hence, we can evaluate the scatter for the assumed
profile, which, independent of observational errors, must be
wavelength-dependent. At each galactocentric radius, we are sampling
different
, taking
advantage of additional information about the
source. For instance, we can take the luminosity profile of a galaxy. We
can assume that for a given radius, the number of stars is roughly the
same (additional information in the form of the geometry of the galaxy
is required). Hence, we can evaluate the scatter for the assumed
profile, which, independent of observational errors, must be
wavelength-dependent. At each galactocentric radius, we are sampling
different

 (L1... Ln)
distributions with different
nsam elements. It is even possible that in the outer
parts, where
(L1... Ln)
distributions with different
nsam elements. It is even possible that in the outer
parts, where  is lower, we
find pixels forming a binomial or extremely
asymmetric distribution. However, the better our sampling of such
distributions, the better will be our characterisation of the population
parameters at this radius. Finally, our results for stellar populations
must be independent of the radius range chosen once corrected for the
radial profile (see
Cerviño et
al. 2008
for details on such corrections). Hence, we can perform a
cross-validation of our results by repeating the analysis by integration
over large radial ranges; this means that we reduce
nsam and increase
is lower, we
find pixels forming a binomial or extremely
asymmetric distribution. However, the better our sampling of such
distributions, the better will be our characterisation of the population
parameters at this radius. Finally, our results for stellar populations
must be independent of the radius range chosen once corrected for the
radial profile (see
Cerviño et
al. 2008
for details on such corrections). Hence, we can perform a
cross-validation of our results by repeating the analysis by integration
over large radial ranges; this means that we reduce
nsam and increase
 . The only requirements
are: (1)
. The only requirements
are: (1)
 must be kept constant in
each of the elements of the sample ; and (2) sufficient
nsam elements are required for correct evaluation of
the variance (c.f. Eq. (10)). The results obtained must also be
consistent with the stellar population obtained using the integral light
for the whole galaxy. Note that if we use SBF we do not need to know the
value of
must be kept constant in
each of the elements of the sample ; and (2) sufficient
nsam elements are required for correct evaluation of
the variance (c.f. Eq. (10)). The results obtained must also be
consistent with the stellar population obtained using the integral light
for the whole galaxy. Note that if we use SBF we do not need to know the
value of
 , but just need to ensure
that it is constant (but unknown) in the nsam elements
used.
, but just need to ensure
that it is constant (but unknown) in the nsam elements
used.
A similar study can be performed using different ways to divide the image. For example, we can take slices of a spherical system and use each slice to compute the variance of the distribution (see Buzzoni 2005 for an example). A similar technique can be applied to IFU observations. The problem is to obtain nsam elements with a similar number of stars and stellar populations that allow us to estimate the scatter (SBF) for comparison with model results. In summary, we can include additional information about the system (geometry, light profile, etc.) in inferences about the stellar populations.
Finally, we can modify the

 (L1... Ln)
distributions to include other distributions representing different
objects. For instance, the globular cluster distribution of a galaxy
(assuming they have the same age and metallicity, in agreement with
Yoon et al. 2006)
implicitly includes a distribution of possible
(L1... Ln)
distributions to include other distributions representing different
objects. For instance, the globular cluster distribution of a galaxy
(assuming they have the same age and metallicity, in agreement with
Yoon et al. 2006)
implicitly includes a distribution of possible
 values. Since these globular clusters have intrinsically low
values. Since these globular clusters have intrinsically low
 values, it is possible that some clusters will be in the biased regime
described in Fig. 7. Since the few
clusters
dominated by PMS stars are luminous, they will be observed and will be
extremely red in colour, even redder than the mean colour of parametric
models (Fig. 8). In addition, there
would be a blue tail corresponding to faint clusters with low
values, it is possible that some clusters will be in the biased regime
described in Fig. 7. Since the few
clusters
dominated by PMS stars are luminous, they will be observed and will be
extremely red in colour, even redder than the mean colour of parametric
models (Fig. 8). In addition, there
would be a blue tail corresponding to faint clusters with low
 comprising mainly
clusters with low-mass MS stars (see
Cerviño and
Luridiana 2004
for more details).
comprising mainly
clusters with low-mass MS stars (see
Cerviño and
Luridiana 2004
for more details).
I finish this section with some rules of thumb that can be extracted from the modelling of stellar populations when applied to the inference of physical properties of stellar systems.
First, the relevant quantity in describing possible luminosities is not
the total mass of the system, but the total mass (or number of stars)
observed for your resolution elements,
 . The other relevant
quantity is the number of resolution elements nsam for
a given
. The other relevant
quantity is the number of resolution elements nsam for
a given
 . The lower the ratio of
. The lower the ratio of
 to nsam,
the better. In the limit, the optimal case is a CMD analysis.
to nsam,
the better. In the limit, the optimal case is a CMD analysis.
Second, the scatter depends not only on
 but also on the age and
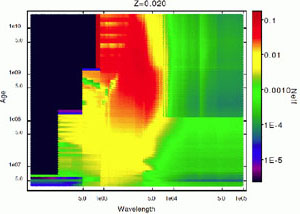
wavelength considered. Fig. 11 shows
Neff values for SSP models with metallicity Z =
0.020 for different ages and wavelengths. As I showed earlier, the lower
Neff is, the greater is the scatter.
Fig. 11 shows that blue optical wavelengths
with
but also on the age and
wavelength considered. Fig. 11 shows
Neff values for SSP models with metallicity Z =
0.020 for different ages and wavelengths. As I showed earlier, the lower
Neff is, the greater is the scatter.
Fig. 11 shows that blue optical wavelengths
with  < 5000 Å
have intrinsically lower scatter than red wavelengths, independent of
< 5000 Å
have intrinsically lower scatter than red wavelengths, independent of
 . The range 5000-8000
Å has intermediate scatter and scatter increases for wavelengths
longer than ~ 8000 Å, depending on the age. In comparison to age
determinations that do not consider intrinsic dispersion (i.e. all
wavelengths have a similar weight), the safest age inferences correspond
to ages between 8 and ~ 200 Myr since variation of
Neff values with wavelength is lower in this mass
range.
. The range 5000-8000
Å has intermediate scatter and scatter increases for wavelengths
longer than ~ 8000 Å, depending on the age. In comparison to age
determinations that do not consider intrinsic dispersion (i.e. all
wavelengths have a similar weight), the safest age inferences correspond
to ages between 8 and ~ 200 Myr since variation of
Neff values with wavelength is lower in this mass
range.
 |
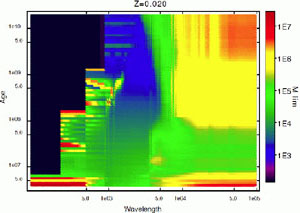 |
Figure 11. Summary of
Neff values (left) and
mean total mass Mlim for
|
|
Fig. 11 also shows the mean total mass for
 1,
1,
 ≤ 0.1 as a function of age and wavelength for Z = 0.020 SSP
models. This is a quantitative visualization of how the average total
mass needed to reach a Gaussian-like regime varies with age and
wavelength. It is evident that blue optical wavelengths reach a Gaussian
regime at a lower average total mass when compared to other
wavelengths. In contrast, red wavelengths not only have greater scatter,
but this scatter is also associated with non-Gaussian distributions for
a wider range of average total mass. Thus, we can strengthen the
statement about age inferences: the safest age inferences correspond to
ages between 8 and ~ 200 Myr if the cluster mass is greater than
105
M
≤ 0.1 as a function of age and wavelength for Z = 0.020 SSP
models. This is a quantitative visualization of how the average total
mass needed to reach a Gaussian-like regime varies with age and
wavelength. It is evident that blue optical wavelengths reach a Gaussian
regime at a lower average total mass when compared to other
wavelengths. In contrast, red wavelengths not only have greater scatter,
but this scatter is also associated with non-Gaussian distributions for
a wider range of average total mass. Thus, we can strengthen the
statement about age inferences: the safest age inferences correspond to
ages between 8 and ~ 200 Myr if the cluster mass is greater than
105
M .
.
Third, the input distributions
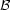 (m0,
t, Z) or IMF and SFH define the output distributions. It
should be possible to obtain better fits (more precise, but not
necessarily more accurate) by changing the input distributions. However,
we must be aware that we have explored the possible output distributions
before any such changes.
(m0,
t, Z) or IMF and SFH define the output distributions. It
should be possible to obtain better fits (more precise, but not
necessarily more accurate) by changing the input distributions. However,
we must be aware that we have explored the possible output distributions
before any such changes.
For instance, low-mass clusters have strong fluctuations around the IMF; each cluster (each IMF realization) could produce an excess or deficit of massive stars. Using the mean value obtained by parametric models, a top-heavy or bottom-heavy IMF would produce a better fit of models and data. Such IMF variations would undoubtedly be linked to variations in age and the total mass/number of stars for a system. However, Monte Carlo simulations can also produce a better fit without invoking any IMF variation. It is possible that Monte Carlo simulations using distributions of different IMFs (e.g. combining IMFs with a variable lower or upper mass limit with a distribution of possible lower or upper mass limits) would produce even better fits. I am sure that the approach using only the mean value is methodologically erroneous. However, it is not clear which of the two solutions obtained by Monte Carlo simulations is the best unless one of the hypotheses (fixed IMF or a distribution combining different IMFs) is incompatible with observational data.
As a practical rule, before exploring or claiming variations in the input parameters, a check is required to ensure that such input parameters are actually incompatible with observational data.
Another issue is how to evaluate scatter outside the SSP
hypothesis. Formally, we may consider any SFH as a combination of
SSPs. Hence, for any SFH scenario evaluated at time
tmod, we can assume that the scatter can be evaluated
using the most restrictive SSP situation in the time range from 0 to
tmod. For instance,
Fig. 11 shows that the ionising flux
( ≲ 912 Å)
requires an average total mass greater than 105
M
≲ 912 Å)
requires an average total mass greater than 105
M to
reach a Gaussian-like regime. Hence, we must ensure that at least
105
M
to
reach a Gaussian-like regime. Hence, we must ensure that at least
105
M has
been formed in each SSP comprising the SFH. Assume that 1 Myr is the
time interval used to define a star formation rate. This implies that
there would be no Gaussian-like distributions for SFR less than 0.1
M
has
been formed in each SSP comprising the SFH. Assume that 1 Myr is the
time interval used to define a star formation rate. This implies that
there would be no Gaussian-like distributions for SFR less than 0.1
M year-1 (i.e. there would be a bias in the inferences obtained
using the mean obtained by parametric models). However, a more
quantitative study of this subject is required.
da Silva et al. (2012)
have suggested additional ideas on the evaluation of scatter including
the SFH.
year-1 (i.e. there would be a bias in the inferences obtained
using the mean obtained by parametric models). However, a more
quantitative study of this subject is required.
da Silva et al. (2012)
have suggested additional ideas on the evaluation of scatter including
the SFH.
Fourth, regarding the output parameters and inferences for time and the total mass/number of stars, we can summarize the following rules:
Use all available information for the system, including previous inferences. However, wavelength ranges used for inferences in the literature must be considered. Additional criteria, such as those in the following points, can be used to evaluate roughly which inferences are more reliable.
Additional information on the system can be obtained from images and other data that, although not used directly in the inferences, constrain the possible range of solutions. Recovery of a complete picture of the system compatible with all the available information should be the aim, and not just a partial picture that can be drawn from particular data.
It is particularly useful to look for the `smoking guns' for age inference: for example, emission lines in star-forming systems imply an age less than 10 Myr ; Wolf-Rayet stars imply an age less than 6 Myr (neglecting binary systems); supernova emission or supernova remnants (from optical, radio or X-ray observations) imply an age less than 50 Myr; high-mass X-ray binaries imply previous supernova events, and hence an age greater than 3 Myr. For instance, Fouesneau et al. (2012) showed that the use of broad-band photometry with narrow-band Hα photometry greatly improves the quality of inferences. However, note that the presence of a `smoking gun' helps to define age ranges, but the absence of smoking guns does not provide information if the mass/number of stars in observations is not known.
Always obtain an estimate of the mass/number of stars in the resolution element. The confidence of an age inference cannot be evaluated unless an estimate of the mass/number of stars of such an age has been obtained (see Popescu and Hanson 2010b for additional implications of this point).
Identify the integrated luminosity distribution regime for the system
considered .  2
fitting including the physical
variance and covariance coefficients is optimal for the Gaussian regime,
but it fails for other distributions. Fig. 11
can be used to identify Gaussianity. For large wavelength coverage, for
which different regimes would be present, rejection of some parts of the
spectra in the fit can be considered; it is better to obtain a less
precise but more accurate result than a very precise but erroneous
result caused by overfitting; in any case, such information can be used
as a guide to obtain a complete picture of the system.
2
fitting including the physical
variance and covariance coefficients is optimal for the Gaussian regime,
but it fails for other distributions. Fig. 11
can be used to identify Gaussianity. For large wavelength coverage, for
which different regimes would be present, rejection of some parts of the
spectra in the fit can be considered; it is better to obtain a less
precise but more accurate result than a very precise but erroneous
result caused by overfitting; in any case, such information can be used
as a guide to obtain a complete picture of the system.
 2
value would be a numerical artefact (e.g. local
numerical fluctuations). For instance, it seems surprising that codes
that infer the SFH using the mean value of parametric models do not
usually quote any age-metallicity degeneracy, although it is present at
a spectral level (c.f. Fig. 10). In fact, it is
an artefact of using only the best
2
value would be a numerical artefact (e.g. local
numerical fluctuations). For instance, it seems surprising that codes
that infer the SFH using the mean value of parametric models do not
usually quote any age-metallicity degeneracy, although it is present at
a spectral level (c.f. Fig. 10). In fact, it is
an artefact of using only the best
 2 fit when results
are presented. Again, I refer to
Fouesneau et
al. (2012)
as an example of how the use of the distribution of possible solutions
improve inferences.
2 fit when results
are presented. Again, I refer to
Fouesneau et
al. (2012)
as an example of how the use of the distribution of possible solutions
improve inferences.