

Bulges are centrally-located stellar distributions with a smooth appearance that manifest themselves as an excess, a bulge, relative to the inward extrapolation of their galaxies outer disk light (Wyse et al. 1997); noting a distinction between obvious bars, nuclear disks and star clusters. The bulk of a disk can be well approximated by the exponential model (Patterson 1940; de Vaucouleurs 1957, 1958; Freeman 1970). In general, they may be comprised of a thick, thin, and super-thin disk (Schechtman-Rook 2013), often display a break and/or truncation at large radii (van der Kruit 1979, 1987; Erwin, Pohlen & Beckman 2008; Hermann 2013), and bars of varying strength appear in some two-thirds of the local disk galaxy population (e.g. Sheth et al. 2013).
Bulges were, for a long time, considered to have R1/4 light profiles (e.g. de Vaucouleurs 1958; Kormendy 1977a; Burstein 1979; Kent 1985; Kodaira et al. 1986; Simien & de Vaucouleurs 1986; Baggett et al. 1998; Lilly et al. 1998; etc.). So popular was the belief in this model that it was referred to as the R1/4 law. However, de Vaucouleurs (1959) had noted departures in some bulge light profiles from his (1948) R1/4 model, and the exponential model was subsequently shown by others to provide better fits for some bulges (e.g. van Houten 1961; Liller 1966; Frankston & Schild 1976; Spinrad et al. 1978). Shaw & Gilmore (1989) and Wainscoat et al. (1989) reiterated that not all bulges are well described with the R1/4 model, and Andredakis & Sanders (1994) showed that many bulges are in fact better fit with an exponential model. Andredakis, Peletier & Balcells (1995) subsequently revealed the suitability of Sérsic's (1963, 1968) R1/n model, which could accommodate R1/4 profiles, exponential (n = 1) profiles, plus everything in between and at either extreme (i.e. n < 1 and n > 4). Furthermore, building on the work with elliptical galaxies by Caon et al. (1993) and Young & Currie (1994), Andredakis et al. provided valuable insight by showing that the bulge Sérsic index correlates with the absolute magnitude of the bulge. Moreover, Balcells et al. (2003) revealed that most early-type disk galaxies do not actually have R1/4 bulges but instead light profiles which have Sérsic indices n < 4.
This year is the golden anniversary of Sérsic's model, which was presented in Spanish by Jose Sérsic 50 years ago. His highly useful R1/n model is reviewed in Graham & Driver (2005). Briefly, the radial surface brightness profiles (see Fig. 1) are such that
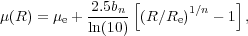 |
(1) |
where µe is the effective surface brightness at the
effective half
light radius Re. The term
bn is not a parameter but a function of the
Sérsic index n such that bn
≈
2n - 1/3, which ensures that Re encloses half
of the model's total light.
The average, or mean, effective surface brightness within
Re is such that
<µ>e = µe
-2.5log[n ebn
 (2n) /
(bn)2n],
and the total luminosity L =
2
(2n) /
(bn)2n],
and the total luminosity L =
2
Re2 < I >e,
where <µ>e = -2.5 log< I
>e.
Importantly, the effective surface brightness is related to the central
surface brightness µ0 in a non-linear fashion
such that
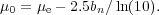 |
(2) |
The impact that the range of bulge light profile shapes has, such as how µe - µ0 and <µ>e - µ0 vary with n, is yet to be fully appreciated within the community. It turns out that this broken homology, i.e. the systematic departures from the R1/4 model as a function of bulge magnitude, has a dramatic influence on the scaling relations we construct using the effective parameters.
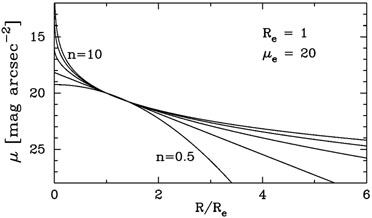 |
Figure 1. Sérsic R1/n surface brightness profiles. Figure adapted from Graham & Driver (2005). |