2. A FEW SELECT DISK GALAXY SCALING RELATIONS

2.1. Insight from elliptical galaxies

Although the bulges of disk galaxies are not simply small elliptical galaxies — because their stellar densities are much higher (see Section 6) — they are similar in the sense that the 3-parameter Sérsic model can describe their light profiles. One can use the luminosity (or rather the absolute magnitude M = -2.5log[L]), central surface brightness and Sérsic index as the three independent variables. From a sample of many elliptical galaxies, Fig. 2 reveals that these parameters follow log-linear relations that unify the dwarf and giant elliptical galaxies across the alleged divide at M_B = -18 mag (Graham & Guzmán 2003). However, when one uses the effective half light parameters (Fig. 3), the continuous, unifying relations are curved. The effective half light radius, and associated surface brightness, have always been somewhat arbitrary quantities. For example, we (astronomers) could have used a radius encolsing 25% or 75% of the total light, and these curved relations would look different again. This would not happen if every light profile was actually an R^1/4 profile. Without this understanding, it had led some to conclude that the dwarf and giant elliptical galaxies must be distinct species due to their apparent, near-orthogonal distribution in diagrams involving the effective parameters. Fig. 3 reveals, for example, how the log-linear M - µ₀ relation (Fig. 2a) maps into the curved M - µ_e relation due to the difference between µ₀ and µ_e seen in Fig. 1 and described by Eq. 2. It also reveals the highly curved nature of the <µ>_e - R_e distribution. As detailed in Graham (2013), this curve shown in Fig. 3c has been derived from the log-linear relations that unify the faint and bright elliptical galaxies in Fig. 2.

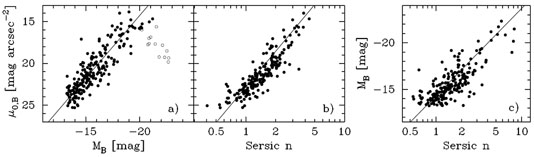Figure 2. The (B-band) magnitude (M = -2.5log[L]), central surface brightness (µ0) and Sérsic index (n) of elliptical galaxies define unifying, continuous, log-linear relations. The deviation at the bright-end of the µ0 - M relation in panel a) is due to the presence of partially depleted cores, thought to have formed from the scouring of binary black holes (e.g. Begelman et al. 1980; Faber et al. 1997; Dullo & Graham 2013, and references therein).

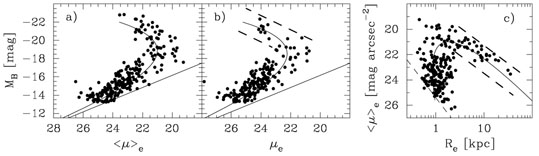Figure 3. The linear relations from Fig. 2 map into curved relations when `effective' parameters (such as Re, µe or <µ>e) are involved. The bright-arms of these curved relations, marked with the dashed lines, are known as the Kormendy (1977b) relation. Figure adapted from Graham & Guzmán (2003) and Graham (2013).

2.2. Bulges

We can use the above insight from elliptical galaxies to better understand the bulges of disk galaxies. Just as there is no dichotomy between dwarf elliptical and giant elliptical galaxies at M_B = -18 mag, or roughly Sérsic n = 2, Fig. 4 reveals no sign of a dichotomy between `classical' n = 4 bulges and n = 1 (or n ≤ 2) `pseudobulges'. One can also see that, as with the elliptical galaxies, the continuous and linear M - n and M - µ₀ relations for bulges map into a continuous but curved M-µ_e relation (Fig. 4c).

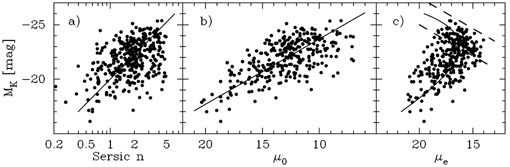Figure 4. Similar to elliptical galaxies, bulges follow single log-linear scaling relations involving absolute magnitude, central surface brightness and Sérsic index. These two log-linear relations shown in panels a) and b) map into the curved relation shown in panel c), which is not a fit to the data shown there but the requirement / prediction from these two log-linear relations. K-band data has been used here from the compilation in Graham & Worley (2008). The bright arm of the curved (absolute magnitude)-(effective surface brightness) relation for bulges in panel c) is delineated by the dashed lines. Figure adapted from Graham (2013).

Although bulges with n 2 will `appear' to deviate from those with n 2 in the M - µ_e diagram, the R_e - µ_e diagram, and also the Fundamental Plane (as noted in Graham & Guzmán 2004, see also Guzmán, Graham & Ismay, in prep.), this is not evidence of a dichotomy but simply reflects that the distribution is curved in diagrams involving effective parameters (see also Graham & Guzmán 2003; Gavazzi et al. 2005; Ferrarese et al. 2006; Côté et al. 2006, 2007).

While rotating bulges with n ~ 1 may be a sign of `pseudobulges' grown from the secular evolution of a disk, some care is needed because Domínguez-Tenreiro et al. (1998), Aguerri et al. (2001) and Scannapieco et al. (2011) have grown bulges with 1 < n < 2 from minor mergers. Further evidence that a radial light distribution with an exponential profile need not have formed from the secular evolution of a disk are the existence of both dwarf elliptical galaxies (Young & Currie 1994) and cD galaxy halos (Seigar et al. 2007; Pierini et al. 2008) which have light profiles with n ≈ 1.