Galactic winds are streams of high speed particles often observed blowing out of galaxies. They are also thought to be the primary mechanism by which energy and metals are deposited into the intracluster and intergalactic medium (see also Sect. 8). Local example of galactic winds are NGC 1569 [341], NGC 253 [172], NGC 6810 [291] and, of course, the archetypal galactic wind in M82 [49]. There is clear evidence for galactic winds in the spectra of several z > 1 galaxies [156]. Probably, the fraction of galaxies experiencing galactic winds was larger at high redshifts [211, 210, 158]. A review of many observational (and theoretical) aspects of galactic winds is given in Veilleux et al. [329].
The mechanical feedback from SNe and stellar winds is the most probable driver of galactic winds in DGs, although other (perhaps accompanying) mechanisms, such as radiation pressure and cosmic rays, are possible and have been put forward [35, 197, 260, 323, 65]. There is a large (and ever growing) number of hydrodynamical simulations of galactic winds in the literature [101, 323, 12, 241]. Many of them, especially in the past, targeted specifically dwarf galaxy-sized objects [59, 60, 261, 58, 159, 194]. A quite common outcome of these simulations is that the energy deposited by SNe and stellar winds creates large bubbles of hot, highly pressurised gas. This gas pushes the surrounding ISM and, under favourable conditions, a large-scale outflow can emerge. If the outflow velocity is large enough, the gas entrained in it leaves the parent galaxy. A galactic wind has been created. If instead the wind velocity is not high enough, the gravitational pull eventually prevails and a galactic fountain is formed instead. Galactic fountains are more likely in large spiral galaxies like our own Milky Way and have been also extensively studied in the past [303, 34, 182, 277, 18]. Given the more reduced gravitational pull, galactic winds are more likely than galactic fountains in DGs. The threshold velocity for the formation of a galactic wind is typically set equal to the escape velocity. However, one should be aware that the motion of gas parcels in galactic winds is not ballistic and the escape velocity can give only an order-of-magnitude estimate of the velocity required to escape the galactic potential well.
Many authors
[145,
324,
56]
have speculated that, since
the binding energy of typical DGs is equal to the explosion energy of
just a few SNe, galactic winds can occur very early in DGs and can
even lead to a quick transition from gas-rich to gas-poor DGs.
However, there are three clear failings of this scenario: (i) it
fails to explain the observed morphology-density correlation (see
Sect. 8), (ii) it fails to explain the
fact that all observed gas-poor DGs of the Local Group possess a large
fraction of intermediate-mass stars (see
[171,
313]
for reviews on
stellar populations of Local Group DGs), (iii) if the galactic wind
occurs very early, Type Ia SNe do not have time to enrich the ISM (see
Sect. 8). Since Type Ia SNe are the major
sources of iron, one would expect very high
[
/Fe] ratios in the
stars of DGs. Exactly
the contrary is observed: stellar populations in DGs are characterised
by very low [/Fe] ratios
[309,
313].
Indeed, many
simulations of the development of galactic winds in DGs cited above
agree on the fact that the fraction of ISM ejected out of a galaxy as
a consequence of a galactic wind must be low. An excellent and still
very relevant review about the effect of galactic winds in DGs is
given by Skillman
[266].
However, hydrodynamical simulations of DGs showed that the galactic winds are often able to expel a large fraction of metals, freshly produced during the star formation activity. This is mostly due to the fact that, if the initial DG gas distribution is flattened (as observed in gas-rich DGs), the galactic wind will preferentially expand along a direction perpendicular to the disk (the direction of the steepest pressure gradient, see also below). Most of the disk gas is not affected by the galactic wind. On the other hand, the freshly produced metals can be easily channelled along the funnel created by the galactic wind. Several papers in the literature have attempted to quantitatively address this point and study the effect of galactic winds on the circulation and redistribution of metals in DGs. The main results of the often-cited work MacLow & Ferrara [159] are that, even in the presence of a strong galactic wind driven by SNeII, the ejection efficiency of unprocessed gas is almost always close to zero. It is different from zero only for the smallest considered galaxies (due to their very shallow potential well). On the other hand, the ejection efficiency of freshly produced heavy elements is almost always close to one. Silich & Tenorio-Tagle [261] found instead that galactic winds do not develop in most of the models, mainly due to the presence of a hot gaseous halo surrounding the galaxy. The effect of off-centred SN explosions and SN explosions distributed over most of the disk was also studied in the literature [79]. Metal ejection efficiencies are reduced in this case, due to more efficient cooling. Wind efficiencies are found to be low even if SN is injected directly into supersonic turbulence [252].
The ejection efficiencies of individual chemical elements was
investigated, too
[226].
As a consequence of very short
starbursts, galactic-scale outflows carry out of the galaxy mostly the
chemical elements produced by dying stars during the most recent
episodes of SF, with large escape fraction of metals with delayed
production, like Fe and N (see also
[322]).
In fact, a significant fraction of
-elements, quickly
produced by SNeII, mix locally before the development of a galactic wind
(see also
[234]).
Metals produced by SNeIa and intermediate-mass stars
can be instead easily channelled along the already-formed galactic
wind and do not suffer much mixing with the walls of the wind. The
situation is much less clear-cut in the presence of multiple bursts of
star formation
[227]
or of complex SFHs
[228].
One should be aware of the fact that turbulence can play a decisive role
in the process of mixing metals, a mechanism usually called turbulent
mixing
[62].
However, it is a considerable experimental,
theoretical, modelling, and computational challenge to capture and
represent turbulent mixing and not much has been done in this
direction for astrophysical flows (but see
[11,
204,
205]).
An estimate of the probability of the development of a galactic wind can be obtained as follows (see [161, 76, 226]). Take for simplicity a source of energy producing a constant luminosity L. Assume also that the density and the metallicity of the ISM is uniform and that its vertical density distribution has a scale height H. The energy input creates a superbubble which is assumed to be spherical and characterised by a radius R. By means of standard, textbook formulas for the evolution of a superbubble without radiative losses (i.e. R ~ t-3/5), the time for the radius R of the superbubble to reach H is readily calculated:
 |
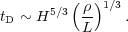(12) |
However, radiative losses, in general, can not be neglected. The radiative losses of the hot cavity can be more relevant for the dynamics of the superbubble than the radiative losses of the shocked material. The cooling timescale of the superbubble can be estimated as:
 |
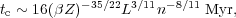(13) |
where L in this formula is in units of 1038 erg
s-1 and n in cm-3. Here,
is a
numerical factor (of the
order of unity) that takes into account the fact that the cooling gas might
be out of ionisation equilibrium. Clearly, if tc is much
shorter than tD, the superbubble loses much of
its pressure before the supershell can reach H and a large-scale
outflow can not occur. By combining Eqs. 12 and 13 one obtains an
approximate criterion for the occurrence of a galactic wind, namely:
 |
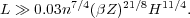(14) |
Although this derivation is quite approximate, the large dependence of the threshold luminosity on H is a solid result. The vertical distribution of gas strongly affects the development of a galactic wind (more than other factors). A galaxy characterised by a very thin disk experiences outflows much more easily than a roundish galaxy. This result matches the physical intuition that in flat galaxies a large-scale outflows easily develops along the direction of steepest pressure gradient (i.e. perpendicularly to the disk), whereas in spherical galaxies the pressure gradient is isotropic and either the outflows occurs along all directions, or the superbubble remains confined inside the galaxy. Indeed, simulations of spherical (or almost spherical) DGs have shown that it is not easy to create galactic winds, even if the energy input is significant [167] or the galaxy does not have a dark matter halo [99, 230]. Although the importance of the disk thickness for the development of outflows was soon recognised, this aspect has not been fully explored in the past in numerical investigation (but see [293, 262, 186, 327, 224, 256]).
 |
Figure 3. Gas density distribution for nine
galaxy models differing on the degree of flattening and the initial
baryonic mass, after 100 Myr of galactic evolution. The first column
represents models with 107
M |
In Recchi & Hensler [223] we specifically addressed the role of gas distribution on the development of galactic winds and on the fate of freshly produced metals. We found that the gas distribution can change the fraction of lost metals through galactic winds by up to one order of magnitude. In particular, disk-like galaxies tend to lose metals more easily than roundish ones. In fact, the latter often do not develop galactic winds at all and, hence, they retain all the freshly produced metals. Consequently, the final metallicities attained by models with the same mass but with different gas distributions can also vary by up to one dex.
Confirming previous studies, we also show that the fate of gas and freshly produced metals strongly depends on the mass of the galaxy. Smaller galaxies (with shallower potential wells) more easily develop large-scale outflows, so that the fraction of lost metals tends to be higher. An example of the results of these investigations is given in Fig. 3. The gas density distribution for nine galaxy models differing on the degree of flattening and the initial baryonic mass, after 100 Myr of galactic evolution is shown in this figure (see figure caption for more details). The effect of geometry on the development of galactic winds is clear from this figure: the density distribution in the models in the bottom row (flat models) is clearly elongated. In one case a galactic wind is already blowing. The models in the upper row are instead still roundish. Clearly, as described before, if a large-scale outflow is formed, freshly produced metals can be easily lost from the galaxy. Any time a galactic wind is formed, the ejection efficiency of metals is larger (some times much larger) than the ejection efficiency of the ISM, confirming that galactic winds must be metal-enhanced. The fact that galactic winds are metal-richer than the global ISM has been observationally verified [170, 201].
The fact that the galactic winds are metal-enriched is a commonly
accepted result. It has been proposed as one of the main mechanisms
leading to the so-called mass-metallicity relation, according to which
the metallicity of a galaxy grows with its mass. Since galactic winds
are metal-enhanced and since DGs experience more easily galactic
winds, clearly one has to expect that DGs are metal-poorer than larger
galaxies
[320,
276].
Although the effect of metal-enriched
galactic winds on the chemical evolution of galaxies might be already
clear from the previous paragraphs, a more quantitative analysis can
be performed, based on simple analytical considerations. Assuming
linear flows, i.e. assuming that infall rates and outflow rates in and
out of galaxies are proportional to the SFR
, a set of
differential equations can be found for the time evolution of the
total baryonic mass Mt, total gas mass
Mg and total mass in
metals MZ within a galaxy (see
[173,
229]):
 |
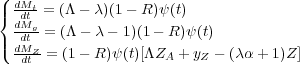(15) |
Here, 
and
are proportionality
constants relating the SFR to the infall and outflow rate,
respectively. ZA is the
metallicity of the infalling material and R is the fraction of the
considered stellar populations locked into long-living stars and
remnants. yZ is the stellar yield, in this case
defined as the ratio between the mass of a specific chemical element
ejected by a stellar generation and the mass locked up in remnants
([312],
see also Sect. 6). Finally,
is the parameter that
takes into account metal-enriched galactic winds, i.e. is the increase of
metallicity of the wind compared to the ISM. Besides this last
factor, the equations are standard, textbook equations for the
simple-model evolution of a galaxy
[312,
203,
174]
and analytical solutions can be found. An analytical solution can be
found even including this further factor
(see Recchi et al.
[229],
eq. 12). If one assumes that the SFR
is
proportional to the total gas mass Mg through a
proportionality constant S (see
Sect. 4), the final result is:
 |
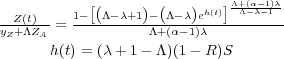(16) |
This solution has been plotted in Fig. 4 for
= 0,
= 2,
S = 1 Gyr-1 and R = 0.26 (from
[346]).
The strong effect of
(a factor of ~ 20)
on the final metallicity of the galaxy is evident from this figure.
Clearly, this kind of modelling can only give an approximate idea
about the chemical evolution of galaxies and that full chemo-dynamical
simulations are required for a deeper insight and understanding of the
metal enrichment process. However, this kind of analytical
calculations are nowadays quite popular, as they enlighten in a simple
way complex correlations among galaxies
[276,
55,
150].
 |
Figure 4. The metallicity of a galaxy, as a
function of time, for models with metal-enriched galactic winds. This
plot shows the solution of Eq. 16 for three different values for the
enrichment parameter
|
of initial
baryonic mass, the middle column shows
the gas distribution for models with mass 108
M