Why is it that such a small fraction of baryons has been converted into stars over the Hubble time? Strong arguments exist, as we have discussed in the previous sections, that an additional process which lowers the efficiency of conversion of gas into stars must be taken into account when considering the cosmological evolution of galaxies. High-resolution numerical simulations have demonstrated the necessity for this process. Energy, momentum and mass deposition from stellar and AGN evolution can have a profound effect on the state of the gas within Rvir, when one considers a simple spherical geometry and their isotropic deposition. Whether this indeed happens when the geometry becomes more complex must be verified. This should be performed by including the by-products of any mechanical feedback on various spatial scales: stellar, AGN and galactic winds, as well as radiative feedback from these objects and from the cosmological background radiation.
A compelling example can be found in the comparison study of disk evolution in a cosmological setting, with and without feedback, (Section 2.1; see also Robertson et al. 2004), where in the absence of feedback the gas quickly violates the Toomre criterion and fragments. Moreover, without feedback there is an overproduction of metals, especially in small galaxies. Even more revealing is the overcooling problem (Section 2.1) which leads directly to the angular momentum catastrophe and involves gas which is bound to the DM substructures, cools down and falls to the centre of the substructure. The latter spirals in to the inner parts of the parent DM halo losing its J via dynamical friction (e.g., Maller & Dekel 2002, and Fig. 10). The gas, therefore, hitchhikes to the bottom of the potential well without being ablated and is deposited there when the substructure is dissolved by the tidal forces, and possibly contributes to the growth of a (classical) bulge.
 |
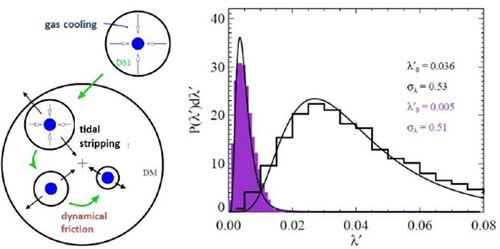Figure 10. Sketch of the overcooling problem (from Maller & Dekel 2002). Left: gas cools down and falls toward the centre of a satellite galaxy which is merging with the main DM halo. Dynamical friction accelerates the process. The cold gas hitchhikes with the sinking satellite and is losing its orbital J but is immune to stripping until the satellite falls to the centre of the parent halo and dissolves there. So gas overcooling leads to the J catastrophe (Section 2). Right: The effect of overcooling on the spin distribution of baryons compared to that of the DM. Baryons (filled curve) being tightly bound at the satellite centre spiral in with the satellite toward the inner parent halo and lose most of J. The figure shows that the J deficiency in baryons is almost a factor of ten. |
Weak feedback has been tested, confirming that such models overproduce the observed baryonic mass function for galaxies, especially for the most and least massive objects (e.g., Keres et al. 2009b). Various `preventive' feedbacks have been used to remove this discrepancy, such as a highly efficient AGN `radio mode' - this did not improve the fit at the high-mass end. Furthermore, it has been impossible to recover the population of massive quiescent galaxies. The overall conclusion is that the solution should come from a more `sophisticated' feedback mechanism which substantially suppresses the star formation in a fraction of galaxies, which increases with mass, while leaving the star formation in the remaining galaxies unchanged.
Galactic bulges may provide a testing ground for our understanding of
angular
momentum redistribution in a forming disk and for various mechanisms that
regulate the star formation. An unexpectedly large fraction, ~ 76%, of
massive, 
1010
M
galactic disks can be fit with a Sersic
index n 
2 and ~ 69% have a B / T mass ratio of
0.2, both in
barred and unbarred galaxies
(Weinzirl et al.
2009).
This result has been obtained from ground-based imaging of a local sample
of 182 galaxies that covers all Hubble types, S0/a-Sm, in the optical
and the NIR. Disks inclined by i
70° have been excluded.
Two-dimensional bulge-disk-bar decomposition has been performed on
H-band images. This result is in stark contrast with predictions
based on the numerical modelling of such objects - only disks that did
not experience a major merger event since z ~ 2 are expected to
have such low B / T ratios. This number is more than an
order of magnitude smaller than the observed fraction of low B /
T disks. Taken at face value, this result points to a serious
contradiction between the observationally detected trend and our theoretical
understanding, and specifically to the role of major mergers in bulge
formation.
This contradiction becomes even stronger in the recent study of the bulge
population within a sphere of 11 Mpc radius using Spitzer
3.6 µm and HST data
(Fisher & Drory
2011).
The dominant galaxy type in the local
Universe has been found to possess pure disk properties, i.e., having a
disky bulge (Section 3.2) or being
bulgeless. The fraction of these
galaxies exceeds 80% of the number of galaxies with a stellar mass of
109
M.
Classical bulges and elliptical galaxies account
for about 25% and disks for about 75% of the total stellar mass within
11 Mpc. Moreover, ~ 2/3 of the star formation in these galaxies occurs in
galaxies with disky bulges. Figure 11
delineates the fractions of various bulge types found as a function of
stellar mass. Below ~ 3 × 109
M,
galaxies are most likely to be bulgeless.
If disky bulges do not originate in mergers (as we have discussed in
Section 3.2), the results of this
analysis reinforce those of
Weinzirl et al.
(2009)
in the most dramatic way.
 |
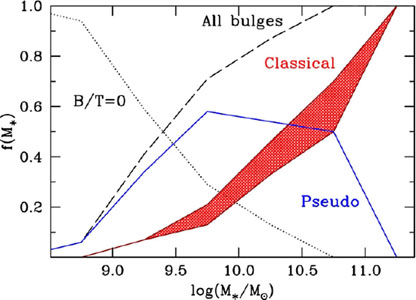Figure 11. Relative numbers of galaxies with classical bulges and elliptical galaxies (red lines), galaxies with disky bulges (i.e., pseudobulges) (blue line), and all disky bulges (black dotted line) as a function of galaxy stellar mass (from Fisher & Drory 2011). |
These results reinforce the opinion that additional physical processes are needed to explain much less massive spheroidal components in disk galaxies.
Feedback, or `feed back', is typically defined as a cause-and-response chain of events that forms a (causal) loop. The loop can be stable or unstable. In simple terms, in the former case, the process repeats itself and we define it as a self-regulated one, and the feedback is negative. In the latter case, the initial conditions for the process are modified and the system must find a new stable loop or disintegrate. In this case the feedback is positive.
In the context of disk evolution, positive or negative feedback can increase or decrease the SFR in a disk. The list of relevant mechanisms is not short and involves radiation (stellar and AGN), winds (stellar, AGN, galactic), AGN jets and backflow cocoons of large-scale relativistic jets, turbulence, SN, bubbles and superbubbles, spiral density waves, stellar and gaseous bars, and cold accretion along cosmological filaments. All the above mechanisms can induce both positive and negative feedback on the SFR. The disk response points to a self-regulation achieved with respect to the star formation process.
As we have discussed in Section 2, the absence of any feedback in disk evolution leads to an overestimate of the spheroidal stellar component. Hence, additional processes must regulate the fragmentation and star formation in disk galaxies. The cause for this can lie beyond the disk itself but fully understanding the disk response is crucial for predicting the feedback loop.
The physics of the various types of feedback is very complex and in many cases, e.g., AGN feedback, not yet fully understood. In some cases, e.g., turbulence, our understanding is mostly empirical. Moreover, many relevant processes, like star formation and turbulence, are well below the resolution limit of current numerical models of galaxy evolution in the cosmological context, and are therefore treated on the subgrid level, i.e., purely phenomenologically. We first discuss the main feedback mechanisms, and then, in Section 6.3, survey the star formation and feedback algorithms used in numerical simulations.
The simplest to model is gravitational feedback, which involves collisional heating of the gas. It occurs during gas-rich mergers. The collision-induced shocks help to virialise gas - a process whose efficiency depends on the orbits of the merger components. Most affected appears to be the low-density gas in the outer parts of the galaxy. The fate of the gas, however, is to remain largely bound to the merger product.
The SN feedback or yield is probably the most analysed in the
literature. We follow estimates by
Dekel & Woo (2003).
Kinetic energies are similar for type Ia and type II SNe, although Ia
are irrelevant here as they deposit their energy away from the star
formation sites. A number of SN explosions resulting from a steady SFR of
*
from gas mass Mgas
embedded in the DM halo of Mvir can be estimated as
 |
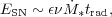(7) |
where 
~
1051 erg is the initial energy released by a
typical SN, 
~ 5 × 10-36 g-1 is
the number of SNe per unit mass of stars (for the Salpeter IMF,
~ 1 per
100 M of
stars), and trad marks the end of the adiabatic phase
and the onset of radiative phase in the SN expansion. The SFR
can be written in terms of the free-fall time as
* ~
M* / tff. So
ESN ~
M*(trad /
tff). In
the relevant range of gas temperatures, a few
× 104 to a few × 105 K, the ratio
trad / tff ~ 10-2 is
constant. In order to expel (unbind) the amount of
gas, Mgas, from a galaxy which has virial velocity
vvir, the
energy released by the SNe should be ESN
0.5
Mgas vvir2 - the binding
energy of this gas. For this to happen, the
velocity of the gas must exceed the critical velocity of
vcrit ~ 0.14
(
M* /
Mgas)1/2 ~ 100 (M* /
Mgas)1/2 km s-1. In other
words, the gas can be removed from DM haloes with virial velocities
vvir
vcrit ~ 100 km s-1, if a large
fraction, say M* ~ Mgas, of
the gas is turned into stars.
The associated DM virial mass which supports the formation of
M* of stellar
mass for such vvir is Mvir ~ 2
× 1011
M, and
the corresponding stellar
mass M* ~ 3-4 × 1010
M, in
apparent agreement
with the bifurcation mass for bimodal evolution discussed in
Section 5.2. So the SN feedback can
reheat the ISM, push it into the halo and even expel a large fraction of
the gas from smaller galaxies. One SN can in principle unbind a giant
molecular cloud. The above estimate makes it
plausible that the gas can be driven out of a galaxy by the SN feedback,
if a large fraction of the original gas has been converted into
stars. But SNe are not very efficient in converting the stellar rest
mass into kinetic energy because fSN
/
100 M
c2 ~ 2.8 × 10-6. While progress has
been made in high-resolution hydrodynamical simulations of SN shells
sweeping up the ISM, the details are not clear yet, especially how
efficiently the energy is distributed among the baryons.
6.2.2. OB stellar winds and AGN feedback
Stellar winds from OB stars are driven by radiation pressure in UV resonance lines of CNO elements and inject about the same amount of kinetic energy over their lifetime as SNe. The asymptotic velocities of these winds are ~ 2000-3000 km s-1. On the subgrid level, these winds from individual stars have been incorporated into numerical simulations (Heller & Shlosman 1994). Understanding the formation of galactic winds under a combined action of OB stars and SNe is more complicated.
AGN winds originate within the central pc - kpc region from the SMBH and are energy- and/or momentum-driven. We limit our discussion here to sub-relativistic winds in radio-quiet QSOs only and exclude the jets. The mechanisms responsible for these winds are based on radiation power, or are hydromagnetically (MHD) driven from the underlying accretion disk (e.g., Blandford & Payne 1982; Shlosman et al. 1985; Emmering et al. 1992; Königl & Kartje 1994). The former can be driven by absorption (scattering) in the resonance lines similar to those in OB stars, and by the dust opacity. The MHD winds can feed on the rotational energy of the disk. Note that the MHD winds are much more efficient in extracting the angular momentum from the underlying accretion disks. Unlike the radiation-driven winds, they can reduce the mass accretion rate substantially - the mass outflow rate in an MHD wind can exceed the inflow rate for some period of time. At the same time, magnetic torques can extract the angular momentum from the disk without much of the outflow at all. This cannot be achieved with the radiatively-driven winds - in order to extract angular momentum from the disk, they must maintain a very high mass flux in the wind. Because this is beyond the scope of our review, we avoid discussing here the magnetorotational instability (MRI) which can generate turbulence and transport J within the disk.
Outflows with clear signatures in UV and optical emission and absorption
lines, and in the radio, have been known for a long time. But reliable
measurements of a mass outflow rate has been obtained only recently,
e.g., for a broad absorption line QSO, SDSS J0318-0600, at ~
120 M
yr-1
(Dunn et
al. 2010).
The kinetic luminosity for this object has been estimated
at ~ 0.001 of its bolometric luminosity, at the lower end of assessments
available in the literature. Powerful molecular outflows from AGN have
been detected with a mechanical luminosity estimated from a few to 100%
of the AGN bolometric luminosity (e.g.,
Reeves et al.
2009).
This means that they cannot be driven by SNe but require a higher efficiency
associated with radiatively-driven winds, or most probably with MHD
winds. It also means that such outflows will deplete the in situ
reservoir of molecular gas in a relatively short time. The molecular
tori observed in type 2 AGN in the NIR can represent the base of
such molecular outflows
(Elitzur & Shlosman
2006).
What is the AGN analogue of the SN feedback efficiency or yield,
fSN,
estimated above? The total energy, EAGN, produced by
an AGN depends on the conversion factor,
AGN ~
0.1, of its accretion energy, i.e., EAGN ~
AGN
M•
c2,
where ~
10-3-1 is the conversion factor of the bolometric
luminosity, Lbol, of the AGN into mechanical
luminosity, and M• is
the mass of the central SMBH. The exact value of
is not
known, and it is expected to depend on the nature of the major
contributor to Lbol, on the ratio of
Lbol to the Eddington luminosity, and
possibly on additional parameters of the flow. We therefore leave
unconstrained and note that in the epoch of galaxy formation at high
redshift, which can be characterised by plentiful fuel supply and high
Eddington ratios for the AGN, the value of
can be as
high as ~ 1. Moreover, if we assume for brevity that the
M•
- 
relation is
maintained at these redshifts (quite unlikely!),
M•
/ M* ~ 10-3 and
 |
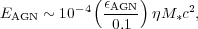(8) |
which means that the efficiency of the high-z AGN is
fAGN ~ 10-4
. This
estimate can be about 10-50 times higher
than fSN, but remains speculative.
The first serious attempt to account for AGN feedback in high-resolution numerical simulations used purely thermal feedback, and no delivery or coupling mechanisms were specified (Springel 2005). A fraction of the isotropic bolometric luminosity of the AGN has been assumed to be deposited locally. Momentum transfer has been ignored. Application of this feedback resulted in limiting the growth of the SMBH and expulsion of the ISM from the galaxy. Less realistic but more detailed simulations have shown that the momentum transfer dominates because of the very short cooling timescales and the inability to retain thermal energy in the dense gas found in galactic centres (e.g., Ostriker et al. 2010). This is also symptomatic of OB stellar winds and winds from accretion disks with effective temperatures in the UV.
So AGN can have a potentially dramatic effect on the ISM and IGM based on their energy output. If this energy, momentum and mass around the SMBHs were distributed in a highly symmetric fashion, this could ensure an efficient coupling with baryons. However, besides direct evidence in the form of collimated jet-ISM/IGM interaction in radio galaxies (both in X-rays and radio bands) and in clusters of galaxies, additional evidence is scarce. Furthermore, the relevant physics of AGN output deposition in baryons is still poorly understood. How exactly is the coupling to baryons achieved? Even when the feedback energy exceeds the gas binding energy, the gas can escape along the preferential directions or via the fluidised bed-type phase transition, dramatically reducing the feedback.
While models based on energy- and momentum-driven outflows have been proposed, these are mostly phenomenological models. The detailed physics of energy and momentum deposition is under investigation now, as well as attempts to translate it into subgrid physics. The important issues involve the driving mechanisms for the wind, their dependence on mass accretion flows, on Eddington ratio, geometric beaming, and additional factors.
While at present there are still theoretical difficulties with almost any type of wind from any object (e.g., star, accretion disk), these winds nevertheless exist and there are clear incentives in working out the corollaries of this existence. The presence of galactic outflows is supported by numerous observations (e.g., Heckman 1994, and references therein). In most cases they are driven by the SNe and winds from OB stars in galaxies that experience starbursts. The contribution of AGN is debatable at present. The driving by the SNe and stellar winds occurs when ejecta of individual sources form a bubble of hot gas, ~ 107-8 K, which expands due to the strong overpressure down the steepest pressure gradient and enters the `blow-out' stage. Besides the mass, energy and momentum injected by such winds, this is probably the main way the highly-enriched material can be injected into the halo and further out into the IGM. The winds appear inhomogeneous and carry embedded cold, ~ 104 K clouds with them, so they represent a multiphase ISM. Their velocities appear correlated with the galaxy stellar mass or its SFR (e.g., Martin 2005).
The overall energetics of these bubbles and superbubbles points to the important and even crucial role galactic winds play in galaxy evolution, from determining the size of galactic disks to regulating the star formation process in galaxies, and removing the overcooling problem discussed earlier. In this context, the overcooling results from under-resolved ISM which will radiate away all the thermal energy deposited by the feedback. The proper resolution must correctly treat the merging of individual SN bubbles producing low-density superbubbles which will remain hot for a prolonged period of time - this resolution is not yet achievable in cosmological or individual-galaxy numerical simulations. Only when small volumes representing a region in the disk are modelled, these processes can be followed. To summarise, any modelling of galaxy formation and evolution must include the development of galactic outflows triggered either by stellar or AGN feedback.
To circumvent this lack of numerical resolution, the necessary physics can be introduced on the subgrid level. We discuss four such algorithms: the constant velocity, the delayed cooling, the blastwave, and the variable wind models.
SF,
above which the star formation is allowed to occur. The SNe directly
heat the ambient hot phase whose cooling timescale is long. This
effectively modifies the equation of state for the ISM. The cold phase
is heated and evaporated via thermal conduction from the hot
phase. Mass-transfer equations between the two ISM phases are solved
analytically. The galactic wind is triggered by modifying the behaviour
of some gas particles into the `wind' particles. The wind particles are
not subject to hydrodynamical forces and experience the initial kick
from the SN. All wind particles have the same constant velocity and the
same mass-loading factor,
w
w /
SF, where
w is the
mass loss in the wind and
SF is the
SFR. The observational constraints on the value of the loading factor
w
are weak.
Rblast. The
timescale for the blastwave to reach this radius is of the order of a
timestep resolution. The blastwave wind model has been efficient in
moving the peak of the star formation to lower redshifts, well beyond
the last major merger, and has significantly reduced the SFR during
mergers due to the feedback in progenitors.
w
defined above and the wind velocity
vw, and both are constrained by
observations. Typically, observations express these two parameters in
terms of the host galaxy stellar mass, M*,
and the SFR. This requires that simulations compute both parameters on
the fly as the model is running and not in the post-processing stage,
which is challenging. In the original version, the outer density of
baryons in a galaxy is limited by 0.01 nSF, where
nSF ~ 0.01-0.1 cm-3 (defined above) is
the threshold for star formation. The value of nSF is
based on the translation of the threshold surface density in the
Kennicutt-Schmidt law, SFR ~
gas
, where SFR is the disk
surface density of star formation,
gas is
the surface density of the neutral gas, and
~ 1-2, depending on the
tracers used and on the relevant linear scales.
In the variable wind model, the wind velocity is calculated as a fraction of
the escape speed from the host DM halo, vw =
vesc,
where =
1.5 for momentum-driven and
= 1 for
energy-driven winds is a scaling factor. The SFR is determined from the
empirical relation with vesc,
 |
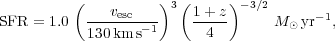(9) |
which is consistent with observations (e.g.,
Martin 2005).
Hence, the wind
velocity is an increasing function of redshift and the SFR. The load factor,
w,
is assumed to represent the energy-driven wind in the low-density
case, n < nSF, and the momentum-driven wind for
n > nSF.
6.3. Feedback and star formation
The physics of isolated stellar, gaseous and gas+stars disks have been analysed extensively over the last few decades by means of analytic methods and numerical simulations. The parallel study of galaxy evolution in a cosmological setting placed emphasis on the initial conditions and on the fact that galaxies are open systems that can exchange mass, momentum and energy with their environment. Under these conditions, the rate of secular evolution can be dramatically accelerated and the direction of this evolution altered significantly. The approximation that galaxies are in dynamical equilibrium remains, except during the merger events.
Probably the most important corollary of studying galaxies in cosmology is narrowing the range of initial conditions and requiring that the evolution complies with them. Understanding that early disks have been much more gas-rich than disk galaxies in the local Universe brings about the natural question of what prevented the full conversion of this gas into stars over the Hubble time. This can be achieved either by keeping the gas at low densities or high temperatures, to prevent the Jeans instability from developing. However, it is difficult to maintain low densities when the gas assembles in disks, unless strong deposition of momentum, energy or both expels the gas from the disk.
Most of the prescriptions for star formation can be followed from
Katz (1992)
with some modifications and involve the Jeans instability. An additional
constraint introduces the critical volume density for star formation,
nSF, which corresponds to the total
Hi + H2 (atomic
and molecular
hydrogen) surface density threshold in the Kennicutt-Schmidt (K-S) law,
SF ~ 3-10
M
pc-2 (e.g.,
Schaye & Dalla
Vecchia 2008).
However, new observational evidence points to a
considerable dispersion in the values of the threshold surface density,
SF and
the slope
, as well as to a
substantial steepening of the K-S law above z ~ 3 (e.g.,
Gnedin & Kravtsov
2011
and references therein). A growing body of evidence points to a
dependence of the SFR on the surface density of the molecular hydrogen,
rather than on the total surface density of the neutral hydrogen.
An intriguing question is whether the Jeans instability in the neutral gas triggers the formation of H2, or whether it is the formation of H2 that triggers the Jeans instability and subsequent gravitational collapse. Current efforts focus on understanding the various factors which regulate the formation and destruction of H2, such as dust abundance and metallicity, UV background, gravitational instabilities facilitating the gas cooling, etc. A fully self-consistent model of the molecular gas balance in the ISM will be developed in the next few years.
We have discussed the mechanisms that are responsible for the feedback from stellar and AGN evolution and pointed out the importance of understanding the ways in which energy and momentum are distributed among the ISM and the IGM. While the sources of energy and momentum operate on very small scales, < 1 pc, compared to characteristic galactic scalelengths and scaleheights, > 1 kpc, they are deposited on much larger scales and can have a global effect. In addition, there is broad agreement between observations, theory and numerical simulations that the multiphase ISM is required to treat the feedback properly.
One possibility for progress in this direction lies in a further increase of the spatial resolution of numerical models, to an extent that at least part of the subgrid physics is in fact simulated, e.g., turbulent cells in the ISM. Sub-50 pc resolution has shown the formation of hot SN bubbles, superbubbles and chimneys, in tandem with turbulent flows there (e.g., Ceverino & Klypin 2009). Galactic winds develop naturally under these conditions, without additional ad hoc assumptions. Unfortunately, such resolution is difficult to achieve in present-day fully self-consistent cosmological simulations.
Another by-product of high-resolution modelling is the possibility of using a much higher threshold for star formation than usual, corresponding to molecular gas. The effect of going to higher critical densities for star formation is shown in Fig. 12, and results in lower star formation efficiencies when averaged over all phases of the ISM. A proper treatment of the cold gas phase is also crucial in order to account for dissipation in supersonic flows. In fact, in order to reproduce the observed log-normal probability density function (PDF) in the ISM, it is necessary to resolve the broad density range, and in particular to resolve the critical density of 105 times that of the average density in the ISM (e.g., Elmegreen 2002). This requirement in tandem with the ISM heating by gravitational instabilities leads to self-regulation, when turbulence limits the efficiency of the star formation process.
 |
Figure 12. Effect of density threshold on star formation. Left: a low-density threshold - a single massive star formation region exists; Right: a high-density threshold. In the latter case, a much smaller region becomes Jeans-unstable and a number of smaller star formation sites exist, resulting in lower star formation efficiencies when averaged over all phases of the ISM. |
Gas-rich disks are prone to fragmentation - the so-called Toomre (1964) instability. The idea of a marginally gravitationally stable gaseous disk was originally proposed by Paczynski (1978), who specifically considered the case of turbulence driven by gravitational instabilities in a disk that was able to cool below Q ~ 1. The resulting turbulent gravitational viscosity was found to be responsible for the disk re-heating, angular momentum transfer and inflow. Analysis and numerical simulations of isolated two-component gas+stars disks indeed have demonstrated the formation of massive clumps that migrate to the centre and heat up the stellar component as a result of dynamical friction, in agreement with analytical estimates (Shlosman & Noguchi 1993; Noguchi 1999). The characteristic timescale for spiraling in toward the central kpc is about a couple of orbital periods. Noguchi (1999) further argued that these clumps contribute to the buildup of galactic bulges.
The developing massive clumps will migrate to the centre over a few dynamical times, while maintained in a marginally stable state with Toomre's Q ~ 1, and contribute there to the bulge growth (e.g., Dekel at al. 2009a). In reality, it is not trivial to stabilise the self-gravitating clumps against runaway star formation. Dekel et al. propose that gravitational interactions between the clumps will also induce turbulence inside the clumps, which will stabilise them against gravitational collapse over the spiralling-in timescale - an interesting possibility so far not verified.
In the cosmological context, including star formation, these clumps, in addition to forming in the disk itself, can be supplied by the incoming flows from cosmological filaments (Heller et al. 2007b; Dekel et al. 2009a; Ceverino et al. 2010). The clumps did, however, show vigorous star formation. Rather than being supported by clump-clump interactions, Heller et al. found that the feedback from stellar evolution has provided support for the clumps, while some of them have been sheared and/or collisionally destroyed before they entered the central kpc. Moreover, the energy/momentum feedback parameter has been varied and the clumps have appeared earlier and have been more numerous in models where this feedback has been smaller. The final bulge-to-disk mass ratio has also shown a clear anti-correlation with the amount of the feedback. Hence, as shown by Heller et al. energy/momentum feedback inside the gas-rich disk delays its fragmentation, and, at the same time, decreases the star-forming activity inside these massive clumps. Internal turbulent pressure in massive self-gravitating clumps can indeed play the role of delaying the star formation, but it is not clear whether it can be driven by the outside turbulence in the disk. The possible internal drivers of turbulence can be their gravitational collapse and energy input from newly formed massive stars and SNe.
Dense molecular clouds in the ISM form via supersonic turbulence in the
ISM. The supersonic velocities decrease on smaller scales as v ~
scale0.5
(Larson 1981),
and may represent a turbulent field dominated by shocks. This
result is supported by numerical simulations of supersonic turbulence
and by analytical calculations (e.g.,
Padoan & Nordlund
2002,
and references therein),
with the possible extention to include the cloud column density, v ~
0.5
scale0.5
(Ballesteros-Paredes
et al. 2011).
The velocity-scale relation may determine the characteristic scale for
gravitational instabilities and sites for star formation. The turbulent
driving comes from the larger scales and dissipation occurs within the
clouds. Recent results show that turbulent motions inside molecular
clouds are driven by gravitational collapse (e.g.,
Ballesteros-Paredes et
al. 2011).