2. INITIAL MASS FUNCTION AND STAR FORMATION

The stellar initial mass function (IMF) is defined as the distribution of stellar masses that form in a given region in one starburst event. Apart from being interesting in its own right, the IMF has important consequences for the observable properties of galaxies. The relative abundance of stars in different mass ranges affects various measurable quantities: most of the stellar mass is contributed by low-mass stars, the luminosity is mainly due to massive stars, while intermediate-mass and massive stars are responsible for enriching the interstellar medium (ISM) with metals. Understanding the physics of star formation and the form of the IMF is therefore crucial for correct interpretation of observations of galaxies. In particular, we would like to have an understanding of the masses of forming stars as a function of the physical conditions in the star formation region, the efficiency of star formation, and its rate.

Historically, the first model of star formation was offered by Newton, who put forward the idea of gravitational collapse.

But if the matter was evenly disposed throughout an infinite space, it could never convene into one mass, but some of it would convene into one mass, and some into another, so as to make an infinite number of great masses, scattered at great distances from one another throughout all that infinite space. And thus might the sun and fixed stars be formed, supposing the matter were of a lucid nature. But how the matter should divide itself into two sorts, and that part of it, which is fit to compose a shining body, should fall down into one mass and make a sun, and the rest, which is fit to compose an opaque body, should coalesce, not into one great body, like the shining matter, but into many little ones; or if the sun at first were an opaque body like the planets, or the planets lucid bodies like the sun, how he alone should be changed into a shining body, whilst all they continue opaque, or all they be changed into opaque ones, whilst he remains unchanged, I do not think explicable by mere natural causes, but am forced to ascribe it to the counsel and contrivance of a voluntary Agent. [Sir Isaac Newton, Letters to Dr. Bentley, 1692]

The next breakthrough was due to James Jeans, who put Newton's conjectures on a more quantitative ground and formulated the criterion of gravitational instability.

We have found that, as Newton first conjectured, a chaotic mass of gas of approximately uniform density and of very great extent would be dynamically unstable: nuclei would tend to form in it, around which the whole of the matter would ultimately condense. [James Jeans, Astronomy and Cosmogony, 1929]

To see how this instability arises, imagine a static infinite medium of density ρ and temperature T with a density fluctuation on a scale λ = 2π / k:

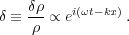(1)

The free-fall time is t_ff ≃ 1 / √Gρ and the dispersion relation is given by:

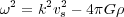(2)

where v_s is the speed of sound in the medium. Exponential growth of the perturbation, and hence instability, will occur for wavelengths that satisfy:

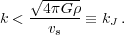(3)

In other words, perturbations on scales larger than the Jeans scale, defined as follows:

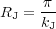(4)

will become unstable and collapse. Note the dependence of the Jeans scale on the density and temperature of the medium. The physical meaning of this criterion is that sound waves must cross the overdense region to communicate pressure changes before collapse occurs. Indeed, a simple way to derive the Jeans scale is to compare the sound crossing time t_sc = R / v_s to the free-fall time of a sphere of radius R. The resulting scale is R_J ≈ t_ff v_s. This simple argument provides us with the typical scale of collapsed objects in a given medium, and serves as the basis for more sophisticated models.

The division of collapsed objects into those that shine (stars) and those that do not (planets) which, as Newton believed, could only be explained by the intervention of a voluntary Agent was described in a very elegant way by Eddington:

We can imagine a physicist on a cloud-bound planet who has never heard tell of the stars calculating the ratio of radiation pressure to gas pressure for a series of globes of gas of various sizes, starting, say, with a globe of mass of 10 gm., then 100 gm., 1000 gm., and so on, so that his n-th globe contains 10ⁿ gm... Regarded as a tussle between matter and aether (gas pressure and radiation pressure) the contest is overwhelmingly one-sided except between Nos. 33-35, where we may expect something interesting to happen. What happens is the stars. [Sir Arthur Eddington, The internal constitution of stars, 1926]

Eddington was the first to suggest that the source of the stellar energy is nuclear fusion of hydrogen into helium. This idea was later confirmed and the theory of stellar nucleosynthesis is now well established. However, a complete theory that describes the process of star formation is still missing. We cannot predict the initial mass function of stars which we shall see is crucial for understanding issues such as feedback. Below we briefly review some of the key aspects of this problem as well as attempts at solving it.

2.1. Star formation: general considerations

Stars form in the dense cores of giant molecular clouds (GMC) - dense and clumpy concentrations of cold gas and dust. According to the Jeans criterion, initial collapse occurs whenever gravity overcomes pressure. Put differently, the important scales in star formation are those on which gravity operates against electromagnetic forces, and thus the natural dimensionless constant that quantifies star formation processes is given by:

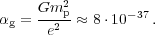(5)

For example, we can derive the maximal mass of a white dwarf star in terms of α_g. For a star with N baryons, the gravitational energy per baryon is E_g ~ -GNm_p² / R, and the kinetic energy of relativistic degenerate gas is E_K ~ p_F c ~ c N^1/3 / R where p_F is the Fermi momentum. Consequently, the total energy is:

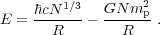(6)

For the system to be stable, the maximal number of baryons N is obtained by setting E = 0 in the expression above. The result is the Chandrasekhar mass:

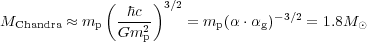(7)

where α = e² / ( c) is the fine structure constant. This simple derivation result is close to the more precise value, derived via the equations of stellar structure for degenerate matter, of 1.4 M.

Another example is the upper limit on the mass of a hydrogen burning star, which can be derived if we compare the radiation pressure P_rad = 1/3 aT⁴ to the thermal pressure of the star, under the condition that the temperature be high enough so as to allow two protons to overcome their mutual Coulomb repulsion. The resulting upper limit is M_Edd ≈ m_p α_g^-5/3 α^2/3 ≈ 50M, which is comparable to the masses of the most massive stars observed (at the Eddington limit, again derived from the equations of stellar structure): ~ 100M.

The formation of a star, or indeed a star cluster, begins with the collapse of an overdense region whose mass is larger than the Jeans mass, defined in terms of the Jeans scale R_J:

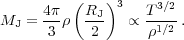(8)

Overdensities can arise as a result of turbulent motions in the cloud. At the first stage of the collapse, the gas is optically thin and isothermal, whereas the density increases and M_J∝ ρ^-1/2. As a result, the Jeans mass decreases and smaller clumps inside the originally collapsing region begin to collapse separately. fragmentation is halted when the gas becomes optically thick and adiabatic, so that M_J ∝ ρ^1/2, as illustrated in fig. 1. This process determines the opacity-limited minimum fragmentation scale for low mass stars, and is given by:

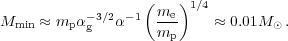(9)

Of course, this number, which is a robust scale and confirmed in simulations, is far smaller than the observed current epoch stellar mass range, for which the characteristic stellar mass is ~ 0.5 M. Fragmentation also leads to the formation of star clusters, where many stars with different masses form through the initial collapse of a large cloud.

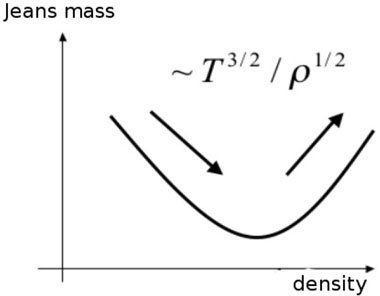Figure 1. Jeans mass vs. density. The minimal Jeans mass sets the limit of fragmentation.

This scenario is confirmed by numerical simulations [1, 2, 3]. For example, fig. 2 shows the formation of a star cluster from an initially spherical molecular cloud with a mass of 100 M. In general, all simulations find that filamentary structures form in the initially smooth cloud before fragmenting further into stars. However, the details of this process, and in particular the relative numbers of stars of different masses depend on the initial density profile of the cloud and the assumed turbulent field that seeded the overdensities.

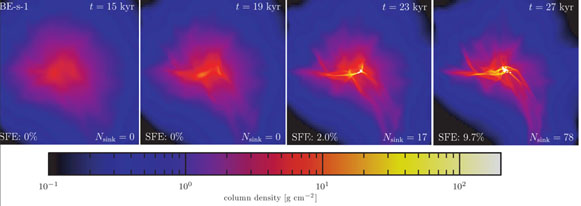Figure 2. Column density in a star forming cloud with an initial ρ ∝ r-1.5 density profile. Each box is 0.13 pc on a side. Figure from [2].

An additional mechanism that can influence star formation is outflowing supersonic winds from a protostar that can accelerate the surrounding molecular gas to high velocities and oppose accretion [4]. These winds can affect the density structure of the cloud [5] and thereby alter the mass spectrum of formed stars and the star formation efficiency [6, 7]. Such outflows have been detected in numerous protostars, and it was found that in some cases they have strong impact on the surrounding medium even at very large distances from the source. For example, the outflows in the Perseus complex have enough power to maintain turbulence and hence halt star formation in their immediate surroundings, but not in the entire complex [8].

Magnetic fields can play an important role in star formation if the mass of the overdense cloud is of the order of the supercritical mass, such that the magnetic energy density is comparable to the gravitational energy density:

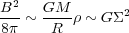(10)

where Σ is the surface mass density. The classical picture is that when the cloud first collapses, its mass must be above the critical mass. Previously, the magnetic field is energetically dominant and halts further collapse. However, magnetic fields are frozen only into ionized gas and dust, whereas neutral matter can continue to accrete onto the cloud. This process is known as gravity-driven ambipolar diffusion. When the mass of the cloud exceeds the critical mass, magnetic pressure becomes irrelevant and the cloud collapses.

Clouds with supercritical values of the magnetic field have been observed in several systems [10], however the question remains whether they play a dominant role in star formation [11]. In particular, the relative importance of magnetic fields and turbulence-driven feedback remains unclear [12].

Molecular clouds are best probed by studying thermal dust emission in the infrared. The Herschel telescope has imaged nearby molecular clouds between 70 µm and 500 µm as part of a survey that is optimized for studying the formation conditions of solar-type stars. The results cover a wide range of environments, from warm to cold cloud complexes, where stars form in clusters or in small numbers or even not at all. Two main results have emerged from these studies. The mass function of prestellar cores has been measured [13]. It is found to match the initial stellar mass function but with a displacement of a factor of about 3 in mass, discussed below. The stellar cores are found to form in long filaments ( 1 pc) of near-universal width ~ 0.1pc, and are fed by what appears to be magnetically-regulated accretion of the surrounding cloud material along striations that are nearly perpendicular to the filaments [14]. The process is inefficient: on GMC scales, only about 2% of the gas is forming stars, whereas in the densest cores, the star formation efficiency exceeds 30% [15]. The peak in the protostellar core mass function at ~ 0.6 M corresponds to the local Bonnor-Ebert mass (the equivalent of the Jeans mass discussed above in the case of net external pressure).

Magnetic fields also cause strong bipolar outflows [16]. These outflows occur because the infalling matter bends magnetic field lines inwards, and the rotating accretion disk leads to field configurations that eject the gas. Numerical simulations that include magnetohydrodynamics [9] indicate that this process results in large-scale outflows, as can be seen in fig. 3. Thus, magnetically-driven feedback reduces star formation efficiency.

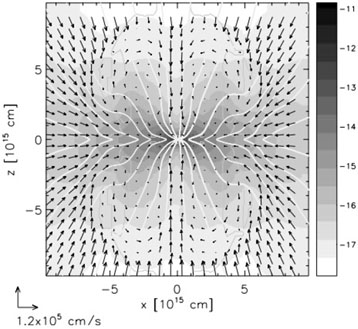Figure 3. Onset of a large-scale outflow in a numerical simulation of collapsing magnetized cloud core. The magnetic pressure drives a bubble that is surrounded by shock fronts and reverses the gas flow. Grey scale shows the density in gr/cm3 (logarithmic). The vector field represents the velocity flow, magnetic flux is in white. Figure from [9].

2.2. The first stars

Since the first stars form in a metal-poor environment, H₂ cooling is dominant, the gas temperatures are relatively high and so is the accretion rate onto the protostar: ~ v_s³ / G ~ 10^-3 M / yr. Thus, the first stars are expected to be extremely massive, reaching ~ 100M and more [18].

A viable feedback mechanism that sets the limit of the most massive first stars is accretion disk evaporation by the ionizing radiation of the protostar. Numerical simulations [17] show that radiation feedback is indeed important in metal-poor stars. The evolution of the accretion rate onto a primordial star with and without this effect is shown in fig. 4. The characteristic first star mass is reduced to ~ 40 M.

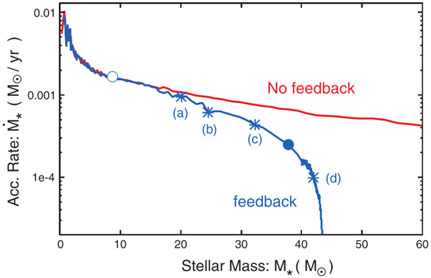Figure 4. Evolution of the accretion rate onto the primordial protostar with (blue line) and without (red line) UV feedback. Figure from [17].

Another possibility to limit the mass of the primordial stars is via gravitational fragmentation. Numerical simulations that followed cloud collapse from cosmological initial conditions demonstrate the possibility of the formation of metal-free binary systems through fragmentation [19].

Cooling controls the lower limit of fragmentation. The cooling in primordial stars occurs via trace amounts of H₂ formation in the parent clouds. This leads to a high accretion rate and high masses, as modulated by feedback. Once enrichment occurs, cooling is dominated either by dust or by atomic cooling. Either pathway, uncertain because we have no robust theory of dust formation in the early universe, allows low mass star formation by fragmentation.

Chemical abundance tracers in the most extreme metal-poor stars testify to the existence of a prior generation of metal-free stars. Numerous metal-poor stars have been detected to date [20]. The abundance and properties of these objects put interesting constraints on the theories of star formation. These expectations can be reconciled with observations, as the most extremely metal-poor solar-mass stars reveal abundance anomalies. The current record holders are two stars at [Fe/H] ~ -5.2 which in common with some ~30% of the extremely metal-poor stars at [Fe/H] ~ -3 are carbon and oxygen-rich [21]. These are the oldest stars ever observed. This means that a previous generation of short-lived, hence massive and essentially zero metallicity, stars polluted the environments where the observed extremely low metallicity low mass stars formed.

2.3. Initial stellar mass function

The initial stellar mass function (IMF) describes all the stars formed in a given region following a starburst. In practice, the IMF is obtained by counting all the stars in a given region and correcting for the most massive stars that by the time of observation had already been transformed into compact objects. This correction procedure was first introduced by Salpeter [22], who obtained a power-law relation in the mass range ~ 0.4-50 M:

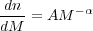(11)

where α = 2.35 and A is a normalization constant. Much recent work has incorporated more sophisticated stellar lifetime modeling and encompassed a wider mass range, resulting in slightly different shapes. For example Kroupa [23] found a broken power-law with α = 0.3 for M < 0.08M, α = 1.3 for 0.08 M < M < 0.5M and α = 2.3 for M > 0.5 M, while Chabrier [24] introduced a log-normal distribution of stellar masses.

Clearly, a complete theory of star formation should be able to reproduce the observed IMF, and some general features can be explained in relatively simple terms [25, 26]. The initial slope is set by the perturbation spectrum and is subsequently modified by the different feedback processes. The broad peak of the IMF is probably determined by the physics of gravitational fragmentation and is due to the dispersion in the thermodynamical properties of the gas. The formation of low-mass stars poses a problem, as they would need to avoid excessive accretion, for example by being ejected from their birth site. High-mass stars form through accretion, and the mass dependence of this process determines the high-mass slope of the IMF.

A complete treatment of the problem is possible only with numerical simulations that can take into account all the relevant physical processes (for an example, see fig. 5). Recent advances in the field and some outstanding problems are discussed in the comprehensive review by McKee and Ostriker [27].

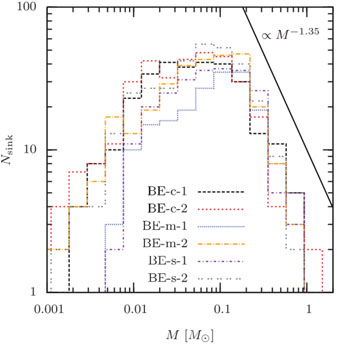Figure 5. IMF (per unit logarithmic mass) for the simulations from fig. 2, for different turbulent fields. The Salpeter slope is shown for comparison. Figure from [2].

A recent development has been the compilation of the mass function of prestellar cores, as discussed above. These are found to be highly embedded in dense molecular clouds, and are identified by Herschel telescope imaging surveys of nearby star-forming complexes and molecular clouds. The prestellar core IMF, shown in fig. 6, has the same shape as the initial stellar IMF, apart from a displacement to larger masses by about a factor of 3 in mass. Both can be fit by a lognormal function. Comparing the peaks of the two functions one infers that the efficiency of star formation is universally, over all masses, a factor of ~ 3. The efficiency factor is most likely due to protostellar outflows, which themselves are usually considered responsible for generating the turbulence observed in star-forming molecular clouds both from simulations, cf. [28] and observations, cf. [29].

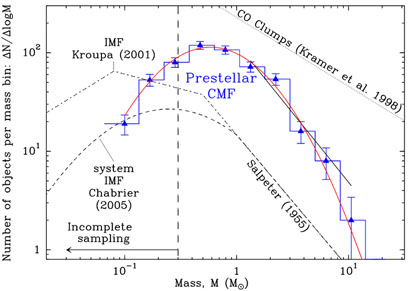Figure 6. Prestellar core mass function in molecular clouds compared to the initial stellar mass function. Figure from reference [15].