4. FROM MASS TO LIGHT: RECONCILING THEORY WITH OBSERVATIONS

4.1. Galaxy luminosity function

The galaxy luminosity or stellar mass function, an example of which is shown in fig. 9, is usually described by the Schechter function [47]:

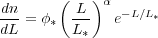(46)

where L_* is the cut-off luminosity. Empirically, L_* is found to correspond to a mass of about 10¹² M at the present epoch. A typical galactic mass is indeed expected from the following considerations [48].

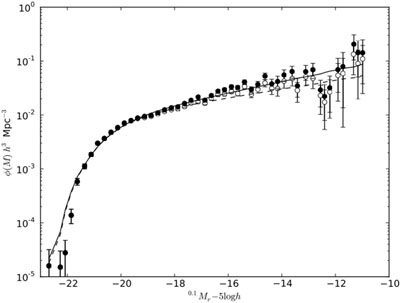Figure 9. Luminosity function measured for low-redshift galaxies (z < 0.1) from the Galaxy and Mass Assembly (GAMA) survey. Solid line shows the fit to the Schechter function. Figure from [46].

Inside the galaxy, the gas generally resides in smaller clumps which collide at the virial velocity. In order for the gas in these clumps to form stars it is necessary that the cooling time of the shocked gas t_cool ~ nk_b T / Λ(T) be shorter than the dynamical time t_dyn ~ 1 / √Gρ. We define the cooling function Λ(T) ∝ T^β for the relevant virial temperature range of the halo (10⁵-10⁷ K), where β ≃ -1/2 for a low metallicity plasma [50]. Then the ratio t_cool / t_dyn is proportional to T^3/2 / ρ^1/2 which in turn is proportional to halo mass. Then the typical mass of stars formed inside the halo is given in terms of the familiar constants α and α_g:

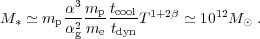(47)

In order to compare the observed luminosity function of galaxies with theoretical predictions, one has to assume a certain mass-to-light ratio (or, equivalently, star formation efficiency). As shown schematically in fig. 10, a single value can be calculated so that the observed and the theoretically predicted curves overlap at M_*. However, their shapes are different, since stellar mass does not necessarily follow halo mass. Assuming a universal mass-to-light ratio leads to too many small galaxies, too many big galaxies in the nearby Universe, too few red massivegalaxies at high redshift and too many baryons in galactic halos. There are additional problems, such as overconcentration and excessive cuspiness in simulated dark matter halos.

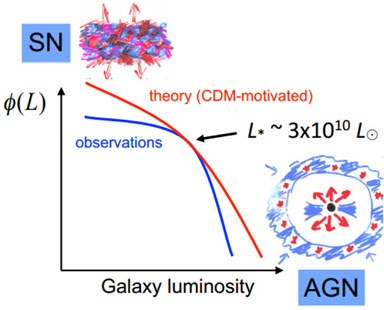Figure 10. The expected (red line) and observed (blue line) galaxy luminosity function. The discrepancies in the low- and high-mass ends is probably due to SN and AGN feedback, respectively. Figure from [49].

The resolution of all these problems must be related to the dynamics of baryons within the dark matter halos, and more specifically the feedback mechanisms that would lower star formation efficiency on various scales. Possible sources of feedback include supernovae, photoionization, massive stellar winds, tidal disruption, input from active galactic nuclei and cosmic reionization. Below we will discuss some of the issues related to feedback, focusing primarily on dwarf galaxies. A more complete treatment is given in several recent reviews [51, 49].

4.2. Supernova-driven winds

One of the possible feedback mechanisms that may suppress star formation is galactic winds driven by the star formation process itself [52, 53]. After an initial population of stars has formed, a certain fraction of those stars (depending on the IMF) explode as supernovae, releasing large amounts of energy into the surrounding medium. If the outflow is accelerated to a velocity that is higher than the escape velocity of the galaxy, it is ejected into the IGM, suppressing the star formation rate. Such outflows have been detected in many systems and are believed to be the primary mechanism by which metals are deposited into the IGM [54].

Whether or not this process can significantly affect star formation efficiency depends on the assumed IMF, the acceleration of the outflow, the manner in which this excess energy is deposited into the IGM and the depth of the potential well of the halo. Multiphase simulations have been able to reproduce supernova-driven winds and trace the metal enrichment processes, but their impact on the star formation efficiency in low-mass galaxies remains unclear [55, 56].

4.3. Entropy barrier

Very low-mass halos (≲ 10⁵ M) are not able to accrete the gas in the first place, because its specific entropy is too high [57]. This imposes a relatively sharp lower limit on the mass of observable dwarfs. Cosmic reionization reinforces this entropy barrier by heating the IGM and suppressing gas infall onto low-mass galaxies [58, 59].

Interestingly, this mechanism is a possible solution to the missing satellite problem, which amounts to the discrepancy between the theoretically expected and observed number of subhalos in a Milky Way (MW)-like galaxy [61, 62]. As we saw earlier, the spectrum of the density fluctuations continues to small scales, and the mass function of DM halos is expected to rise steeply towards low masses. The majority of these halos fall into more massive structures, and some are gravitationally disrupted. However, numerical simulations predict that a significant fraction of these subhalos survive. The problem is that the number of subhalos produced in numerical simulations greatly exceeds the number of observed dwarf satellites in the MW and the Local Group.

One way to resolve this problem would be to modify the spectrum of the primordial density fluctuations, so as to reduce the power on small scales, for example by introducing warm dark matter. However, other possibilities exist within the framework of CDM, such as mass-dependent suppression of star formation. In the latter scenario, which however lacks any convincing physical mechanism, the expected satellites exist but are not observed. Semi-analytic models of galaxy formation that account for an entropy barrier created after reionization are able to reproduce the observed present epoch luminosity function [60], as shown in fig. 11. However these models, if tuned to the faint dwarfs, underpredict the numbers of massive dwarfs.

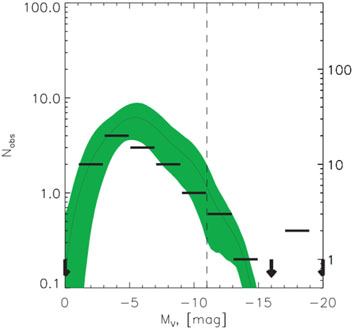Figure 11. MW satellite magnitude distribution (bars) and predictions from a semi-analytic model with mass-dependent suppression of star formation. Figure from [60].

4.4. Tidal disruption

Some of the satellites may be tidally disrupted due to close encounters with more massive subhalos or during infall into the main halo, if their orbits intersect the disk or bulge. In this case, distinct stellar structures in the outskirts of the more massive systems are expected, and these are indeed observed in deep images of nearby galaxies, as shown in fig. 12. The origin of these tidal tails is confirmed by numerical simulations [63]. An independent confirmation of the origin of these structures is the fascinating discovery of gaps in the tidal tails around the outermost MW globular star clusters [64], which indicate the presence of dark satellites. This effect is also predicted by numerical simulations [65].

Figure 12. Deep image of the stellar tidal stream around NGC 5907. Figure from [66].

These galactic fossils can shed light on the hierarchical evolution of the host halo. The galactic archeologist can, in principle, reconstruct the history of the MW by observing the surviving dwarf galaxies and the debris of those that perished [67]. Both populations should be explained by a viable theory of galaxy formation, since the same processes are responsible for the formation of present-day as well as high-redshift dwarfs.

4.5. The core/cusp problem

Another problem in the standard theory of galaxy formation is related to the density profiles of dark matter halos. Numerical N-body simulations predict a universal profile which diverges toward the halo center as ρ ~ 1/r [68]. However, observations reveal flat central profiles in dwarf and low surface brightness disk galaxies [69].

A possible solution of the core/cusp problem may lie in supernova-driven gas outflows [70]. In this scenario, fast and repeated gas outflows following bursts of star formation transfer energy to the dark matter component and flatten the density profile of the halo [71]. As shown in fig. 13, galaxies form with a steep profile which significantly flattens over cosmic time. Cusps are retained only in very small galaxies, where the star formation rates are too low to significantly modify the density profile [72]. Therefore, this model predicts the existence of observable small cuspy galaxies.

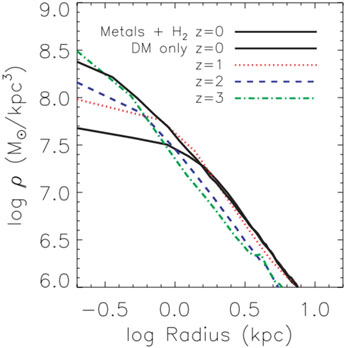Figure 13. The DM density profile of a simulated dwarf galaxy at different redshifts. In the DM only simulation, the galaxy retains its cuspy profile, whereas in the run with repeated outflows a shallow inner profile is formed by z = 0. Figure from [70].

It has indeed been shown [73] that at the high halo mass end, above M_halo ~ 10^11.2 M, the deepened potential well induced by the greater efficiency of star formation is able to resist the expansion process, and such massive galaxies become increasingly cuspy. This paper used a suite of hydrodynamical simulations from the MaGICC project [74] that well reproduce many observed galaxy relationships over a wide stellar mass range [75], and make predictions for the relation between the inner slope of DM density profiles and galaxy mass: they found, in particular, that the effect of baryons on the dark matter halo depends on the integrated efficiency of star formation M_⋆ / M_halo in the way shown in fig. 14. At the low mass end, their prediction is in agreement with previous studies, and at the high mass end the profiles steepen again due to the increased stellar mass at the galaxy center that oppose the expansion process. The flattest slope is found at M_halo ~ 10^10.8 M, or V_rot ~ 50 km/s in agreement with the most reliable observational measurements of cored profiles in disc galaxies, found in low surface brightness (LSB) galaxies with V_rot < 100 km/s [76].

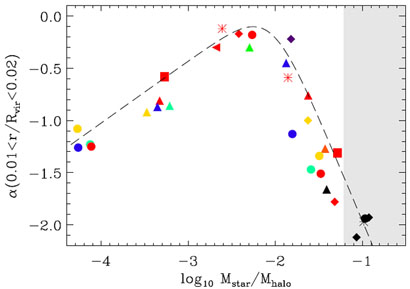Figure 14. The relation between dark matter density profile slope α, measured between 0.01 < r / Rvir < 0.02, and the stellar-to-halo-mass ratio of each simulated galaxy. Figure from [73].

4.6. Cosmic reionization by dwarf galaxies

The very steep slope of the faint end of the galaxy luminosity function, as measured in very deep surveys [77], raises the possibility that the universe was reionized by dwarfs (see fig. 15). Star-forming galaxies are the most obvious source of ionizing photons, and it seems plausible that dwarfs, which outnumber large luminous galaxies, could produce enough UV photons to reionize the Universe [77, 78]. Under reasonable assumptions about the escape fraction of photons and the clumping factor of the intergalactic medium, and the requirement that a low level of star formation extends out to redshift ~ 12, the optical depth to reionization by early low-luminosity galaxies as seen to z ~ 8 is marginally consistent with the constraints of cosmic microwave background measurements [79].

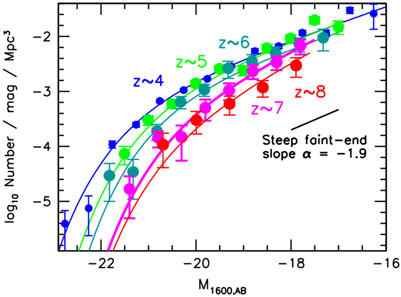Figure 15. UV luminosity functions from Hubble Ultra Deep Field observations. Figure from [77].

However observations suggest that the UV rest-frame stellar luminosity density may drop sharply beyond z ~ 8 [80], which would reduce the possible contribution of ionizing photons at the epoch when they are most needed.