Annu. Rev. Astron. Astrophys. 2013. 51:393-455 Copyright © 2013 by Annual Reviews. All rights reserved

7. THE INITIAL MASS FUNCTION

The stellar IMF is of fundamental importance for many areas of astrophysics. The form of the IMF is well-constrained in the Galactic disk (Salpeter 1955, Miller & Scalo 1979, Kroupa 2001, Chabrier 2003). However, it is not clear whether the IMF has had the same form over all of cosmic time and in all environments. The low mass end is of particular importance, as ~ 60-80% of the stellar mass density in the Universe is in the form of stars with masses < 0.5 M_⊙. Low mass stars are very faint and so contribute only a few percent to the integrated light of an old population. For this reason, when fitting the SEDs of galaxies, an IMF is typically assumed, and so the IMF is one of the largest sources of systematic uncertainty in studies of extragalactic stellar populations.

It has been known since at least the 1960s that dwarf-sensitive and, to a lesser degree, giant-sensitive spectral features could be used to count the number of low-mass stars in the integrated light of old stellar populations (e.g., Spinrad 1962, Spinrad & Taylor 1971, Whitford 1977, Frogel et al. 1978, Frogel, Persson & Cohen 1980, Vazdekis et al. 1996, Schiavon, Barbuy & Singh 1997, Schiavon et al. 1997, Schiavon, Barbuy & Bruzual A. 2000). This idea is limited to quiescent systems because the massive stars associated with ongoing star formation would dramatically outshine the faint low mass stars. The fundamental difficulty then, as now, is the separation of abundance effects from giant-to-dwarf ratio effects. Both effects can change the strength of the gravity-sensitive lines.

Spinrad & Taylor (1971) concluded that the nuclei of the nearby galaxies M31, M32, and M81 are dominated by dwarfs, with an implied M / L = 44. These conclusions were based on photoelectric scanner observations reaching to 1 μm . Subsequently, Cohen (1978) measured the IMF-sensitive Na i, CaT, FeH and TiO features in the nucleus of M31 and M32 and concluded that an IMF comparable to that of the solar neighborhood was favored, along with metallicity enhancement in M31. Faber & French (1980) also measured the strength of the Na i doublet in M31 and M32 and instead argued for a dwarf-rich IMF, along the lines of Spinrad & Taylor (1971), with M / L_B = 28. Frogel et al. (1978) analyzed optical-NIR colors and the CO bandhead at 2.3 μm for 51 early-type galaxies and concluded that dwarf-rich IMFs were inconsistent with the data and favored models with M / L_V < 10. With updated detector technology and more sophisticated models, Carter, Visvanathan & Pickles (1986) argued against dwarf-rich IMFs on the basis of the Na i, CaT, TiO and FeH features in 14 elliptical and lenticular galaxies. Their results implied mass-to-light ratios of M / L ~ 6. In a series of papers, Hardy, Couture and collaborators (Hardy & Couture 1988, Delisle & Hardy 1992, Couture & Hardy 1993) analyzed the IMF features Na i and FeH for of order a dozen galaxies and concluded that dwarf-rich IMFs were strongly disfavored. Measurements of the FeH band at 1 μm (also known as the Wing-Ford band) were particularly important, as this feature becomes very strong for IMF exponents steeper than Salpeter (Whitford 1977).

Early work aimed at measuring the IMF from integrated light spectra suffered from serious limitations, including (1) the lack of accurate stellar evolution calculations across the main sequence and through advanced evolutionary phases; (2) the use of empirical stellar spectra collected from the solar neighborhood, which implied that the effect of non-solar abundance ratios could not be adequately assessed; (3) poor NIR detector technology, which made it very difficult to measure red spectra at the sub-percent level precision necessary to measure the low-mass IMF in integrated light. These limitations contributed to the wide range of reported IMF exponents and mass-to-light ratios noted above. In the past two decades, each of these limitations has been significantly reduced, though not eliminated. Stellar evolution calculations have improved dramatically since the 1970s, the response of stellar spectra to elemental abundance variations has been studied in detail (e.g., Tripicco & Bell 1995, Korn, Maraston & Thomas 2005, Serven, Worthey & Briley 2005, Conroy & van Dokkum 2012a), and NIR detector technology has steadily improved.

The debate over IMF variation was renewed by Saglia et al. (2002) and Cenarro et al. (2003), who independently reported an anti-correlation between the strength of the IMF-sensitive CaT index and velocity dispersion for elliptical galaxies. Comparison to SPS models with solar-scaled abundance ratios required dwarf-rich IMFs, with an exponent of α ≈ 4 at the highest dispersions (compared to the Salpeter value of 2.35). Saglia et al. (2002) argued against this interpretation, as such a steep IMF would imply M / L ≈ 40, well in excess of newly available dynamical constraints. Worthey, Ingermann & Serven (2011) investigated several calcium-sensitive spectral features, and concluded that a modest decrease in [Ca/Fe] with velocity dispersion could also explain the observed trends. Worthey, Ingermann & Serven (2011) also noted that such dwarf-rich IMFs would yield optical-NIR colors (e.g., V - K) much redder than even the reddest observed early-type galaxies.

An IMF different from the Galactic disk (often referred to as a non-universal IMF) was also reported by van Dokkum & Conroy (2010) based on the analysis of high S/N spectra extending to 1 μm for eight massive galaxies in the Coma and Virgo galaxies. These data were of extremely high quality thanks to new detector technology installed on the Low Resolution Imaging Spectrometer (LRIS) instrument at the Keck Telescope. The data were interpreted with new models limited to solar-scaled abundance patterns. Dwarf-rich IMFs were favored, with an IMF exponent in the range 2.3 < x < 3. It is worth pausing here to note that the meaning of `dwarf-rich' has evolved over the years. In the 1970s dwarf-rich IMFs indicated mass-to-light ratios exceeding 20, often reaching as high as 40. With the IMF in the solar neighborhood now well-established (Kroupa 2001, Chabrier 2003), the reference point has shifted. Now, `dwarf-rich' IMFs are those that contain relatively more low-mass stars than found in the solar neighborhood and would indicate, amongst other implications, a non-universal IMF. In this sense, the Salpeter IMF is `dwarf-rich', as it contains more low-mass stars than the Kroupa (2001) IMF for the solar neighborhood.

Conroy & van Dokkum (2012b) were the first to analyze high-quality absorption line spectra of 34 early-type galaxies and the nuclear bulge of M31 with a model that allowed for both IMF variation and abundance pattern variation (in addition to variation in age and several nuisance parameters). The model, presented in Conroy & van Dokkum (2012a), allows for variation in the abundance pattern of 11 elements, and is based on the latest isochrone tables and the MILES and IRTF stellar libraries. Conroy & van Dokkum (2012b) simultaneously fit the full blue and red galaxy spectra to their models, including the classic IMF-sensitive features Na i, CaT, and FeH, as well as IMF-sensitive features in the blue spectral region. An example fit to a massive early-type galaxy is shown in Figure 14. They argued that the models favor IMFs that become progressively more dwarf-rich (i.e., more bottom heavy) for more massive and more α-enhanced galaxies. Over the full sample, the mass-to-light ratios predicted by their best-fit IMFs vary by only a factor of 3 at fixed age and metallicity. The IMF variation advocated by Conroy & van Dokkum (2012b) is thus much subtler than previous claims for dwarf-rich IMFs. The best-fit mass-to-light ratios do not violate dynamical constraints. Similar conclusions were reached by Smith, Lucey & Carter (2012) based on the analysis of 1 μm spectroscopy of 92 galaxies in the Coma cluster, and by Spiniello et al. (2012), who analyzed indices sensitive to Na i and TiO for a sample of early-type galaxies.

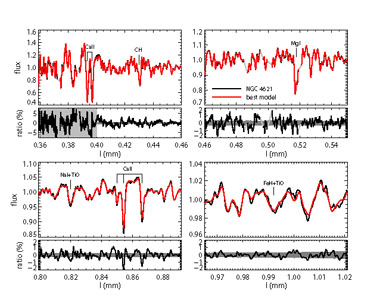Figure 14. Comparison between the best-fit model and observed spectrum for NGC 4621, a massive early-type galaxy. Both data and model have been continuum normalized. The S / N is indicated as a grey shaded band; the data at < 4000 Å were not included in the fit but are included here for completeness. The model has 21 free parameters including the abundance of 11 elements and the shape of the low-mass IMF. The rms difference between the model and data is 0.8%. IMF-sensitive features include the Na i doublet at 0.82 μm, the Ca ii triplet at ≈ 0.86 μm , and the FeH bandhead (i.e., the Wing-Ford band) at 0.99 μm . The best-fit M / L is ≈ 2 × as large as would be expected for a MW IMF, suggesting that the IMF is not universal. From Conroy & van Dokkum (2012b).

Meanwhile, there have been several less-direct arguments favoring top-heavy (or bottom-light) IMFs in some types of galaxies and in some phases of a galaxy's evolution. Tinsley (1980) suggested that a constraint on the IMF near the turn-off mass could be obtained by comparing the evolution of the M / L ratio and color of passively evolving galaxies. van Dokkum (2008) applied this idea to the evolution of galaxies on the fundamental plane, and found evidence that the IMF is flatter than the MW IMF at ~ 1 M_⊙ in early-type galaxies. However, van Dokkum & Conroy (2012) demonstrated that when galaxies are compared at fixed velocity dispersion, as opposed to fixed stellar mass, the evolution in the fundamental plane is consistent with the standard Salpeter slope at ~ 1 M_⊙ (see also Holden et al. 2010). Numerous authors have demonstrated that the evolution of the cosmic star formation rate and cosmic stellar mass density are mutually inconsistent but can be brought into agreement by adopting a top-heavy IMF (Hopkins & Beacom 2006, Davé 2008, Wilkins, Trentham & Hopkins 2008). However, recent improvement in the modeling of the data, including luminosity-dependent dust corrections, rising SFHs, and revised values of the faint end slope of the mass function have reconciled the cosmic star formation and mass densities derived with standard IMFs (Reddy & Steidel 2009, Papovich et al. 2011, Behroozi, Wechsler & Conroy 2012). A third argument in favor of top-heavy IMFs is the apparent inability of galaxy formation models to reproduce the observed number of luminous submillimeter galaxies (Baugh et al. 2005). Here too recent observations and more sophisticated models have significantly reduced the tension between models and data (Hayward et al. 2012). It thus appears that much of the evidence originally favoring a top-heavy IMF at certain epochs and under certain conditions can now be explained by more mundane effects.

7.1. Summary

Extremely dwarf-rich IMFs are now routinely ruled out both by sophisticated SPS models and dynamical constraints, and earlier evidence for top-heavy IMFs has not held up to further scrutiny. However, more modest IMF variations appear to be supported by the data, at the level of a factor of 2-3 in M / L. It is intriguing that constraints on the IMF based solely on dynamical modeling also favor a mild steepening (i.e., relatively more low-mass stars) with increasing velocity dispersion (Treu et al. 2010, Auger et al. 2010, Graves & Faber 2010, Spiniello et al. 2012, Thomas et al. 2011, Sonnenfeld et al. 2012, Cappellari et al. 2012, Dutton, Mendel & Simard 2012, Dutton et al. 2012a, 2012b). As both dynamical and stellar population-based techniques suffer from non-negligible but largely orthogonal systematics, the most promising direction for future constraints will come from joint analyses of the same systems with SPS and dynamical techniques.