Stellar feedback involves the insertion of matter, momentum and energy from stars into the surrounding fluid, from which the stars may also still be accreting gas. In terms of material, momentum and energy emitted per star, massive OB–type stars far outweigh their lower–mass brethren in importance. In clouds where there are no O–stars (either because the cloud mass is too small to support massive star formation, or because there has not been time for O–stars to form), feedback from low– and intermediate–mass stars in the form of jets and outflows and the conversion of gravitational potential energy to heat are dominant processes. On larger lengthscales and longer timescales, encompassing the formation and evolution of galaxies and cosmic star formation, it is again the O–stars that dominate the stellar contribution to feedback, but the other smaller–scale processes may still have influence, since they help determine the environments in which the O–stars are born.
The physics of photoionisation were first elucidated in detail by Strömgren, (1939) and an excellent modern introduction can be found in sterbrock and Ferland, (2006). If a source of QH ionising photons per second ignites in a cloud with initial number density n0 atoms cm−3, the number density of ions ni will also initially be equal to n0. If the cloud is pure hydrogen and overall electrically neutral, the electron number density ne must equal the ion number density, so we have ne = ni = n0.
As the ionisation front moves outwards, more photons are consumed by recombinations behind it. The recombination rate per unit volume is given by α ne ni = α n02. Recombinations directly to the ground state produce photons which are able to ionise another atom elsewhere in the nebula. However, since a recombination of this kind quickly produces another ion, their overall effect can be neglected to first order, which is known as the ‘on–the–spot' (OTS) approximation. Only recombinations to states other than the ground state consume stellar photons, and this rate is given by αB n02, αB being the recombination rate to all states above the ground state.
Eventually, the total recombination rate behind the ionisation front equals the rate at which the source produces photons, so no more neutral gas can be ionised. This state is known as the Strömgren sphere, described by the Strömgren radius Rs, satisfying
 |
(1) |
The ionised gas inside the Strömgren sphere has a temperature determined by the equilibrium of heating and cooling processes. The main heating process is the absorption of stellar photons. In a nebula with solar metallicity, the main coolants are optical line emission from metals, with some contribution from free–free emission. These process equilibrate at 8 000 – 10 000K, although this temperature may be higher in low-metallicity environments where line cooling is less efficient. Since the temperatures of neutral clouds lie in the range 10–100 K, the Strömgren sphere will be vastly overpressured and will expand supersonically. This process was first studied by Spitzer, (1978), who derived the well–known relation for the radial evolution of the shock driven by the expanding HII region
 |
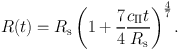(2) |
Later, Franco et al., (1990) considered the case of HII regions expanding in clouds with radial density gradients ρ(r) ∝ r−n. They showed, in particular, that if n > 3/2, the ionisation front will inevitably overtake the shock front and ionise the whole cloud, regardless of its mass. Early 2D numerical work by Garcia-Segura and Franco, (1996) found that expansion of ionisation fronts in density gradients, and in uniform clouds, was accompanied by the formation of fingers of dense neutral material reaching into the HII region, reminiscent of observed pillars/elephants' trunks. They interpreted these structures in terms of the generic ionisation front instability analysed by Giuliani, (1979).
2.2. Main–sequence line–driven winds
The powerful fluxes of energetic photons emitted by OB stars are able to
accelerate line–driven winds in their atmospheres. Material
leaves the surface of the star at a velocity which asymptotically
approaches the wind terminal velocity v∞, of
order 103 km s−1 for a main–sequence
O–type star
(Lamers and
Cassinelli, 1999).
The wind mass fluxes 
for such stars are typically
∼10−5 M⊙
yr−1 but can approach
∼ 10−4 M⊙
yr−1.
The effect of the wind depends sensitively on the thermodynamics of the
shocked gas inside the wind bubble. The extremal assumptions are (i)
that all the mechanical energy is retained by the bubble and the
expansion is adiabatic, or pressure driven, in which case
R(t) = (L / ρ0)1/5
t3/5, and (ii) that cooling is maximally efficient,
whence R(t) =
[2
v∞ / (3ρ0)]1/4
t1/2. Note in both cases the very weak dependence on
the both the stellar properties and the density of the background
medium. The reality is much more complex and lies somewhere between
these extremes. More sophisticated models were first computed in 1D by
Castor et
al., (1975),
Weaver et
al., (1977)
who examined the influence of thermal conduction between the hot shocked
wind and the cool swept–up ISM and the corresponding evaporation
of ISM material into the wind bubble, which rapidly comes to dominate
its mass.
Koo and
McKee, (1992a)
and
Koo and
McKee, (1992b)
discuss in exhaustive detail the realistic case of partially radiative
bubbles.
Recently, Rosen et al., (2014) have attempted to evaluate the importance of these processes observationally by totting up the energy inserted by winds and that lost by various physical processes (radiative cooling, mechanical work, thermal conduction, gas–grain interactions) in four star–forming regions – 30 Doradus, Carina, NGC 3603 and M17. They concluded that radiative cooling and mechanical work are unimportant, except in the case of M17 where work done on the cold gas can account for 38% of the injected wind energy. Adding thermal conduction and gas–dust cooling can account for the remainder of the input energy, but only if rather extreme assumptions are made. They instead infer that large fractions of the wind energy is lost via bulk leakage of hot wind gas, or small–scale mixing with the cold gas.
The lifetimes of the most massive stars are comparable to or shorter than the inferred lifetimes of GMCs, so at least some of these stars are likely to enter the final stages of their lives while embedded in their natal clouds. The effects of exotic evolutionary phases such as LBV and WR stars have generally not been considered in GMC–scale simulations owing to the expense of simulating the long timescales involved.
The WR stage profoundly alters the properties of the wind of a massive star. The mass loss rate increases dramatically to ∼ 10−4 − 10−3 M⊙ yr−1 as the star sheds its outer layers, and the terminal velocity correspondingly declines to ∼ 100 km s−1. A thorough introduction to these and other kinds of stellar wind can be found in Lamers and Cassinelli, (1999).
Understanding the effects of photoionisation and winds clearly relies on knowing how the ionising photon luminosity and wind mass loss rate and terminal velocity vary as a function of stellar age and mass. There are several observational studies of this issue, such as Smith, (2006) or Weidner and Vink, (2010).
Photoionisation and winds have traditionally been the most popular feedback mechanisms, perhaps since their effects are readily observable as ∼ 10pc bubble structures in atomic emission lines, radio continuum and infrared dust emission. Several authors have considered which of the two should be more important (e.g. Capriotti and Kozminski, 2001, Matzner, 2002), generally concluding that expanding HIIRs are more damaging.
When massive (> 8 M⊙) stars exhaust their core hydrogen, a chain of events ensues which eventually results in a supernova explosion. The timescale on which hydrogen exhaustion occurs depends on the stellar mass. For a 10 M⊙ star, it is ≈ 30 Myr, but for the most massive stars, it may be as short as ≈ 5 Myr, comparable to or shorter than the lifetimes of GMCs. The supernova explosion results in the ejection of ∼ 10 M⊙ of metal–enriched material at speeds of ≈ 3 × 103 km s−1, carrying approximately 1051 erg of total energy. In the classic problem of the point deposition of energy in a uniform medium, the supernova remnant passes though a brief ‘free–expansion' phase until the mass swept up becomes comparable to the ejecta mass, before entering the adiabatic Sedov–Taylor phase, during which the blast wave radius evolves with time as
 |
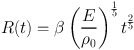(3) |
where β is an order–unity constant. The Sedov–Taylor phase ends when the cooling timescale becomes shorter than the expansion timescale and the supernovae remnant enters the radiative phase. In reality, the evolution of a supernova blastwave is likely to be much more complex, since it in reality encounters the interior of a wind bubble/HII region, rather than a smooth ambient medium. A comprehensive review of the expansion of astrophysical shock– and blast– waves, including the cases of nonuniform background density fields, is given by Ostriker and McKee, (1988).
Much of our understanding of the evolution of massive stars is predicated on the assumption of single stars evolving in isolation, owing to the extreme difficulty of assuming otherwise. However, a large fraction (45–75%) of massive stars are members of binaries (usually with other massive stars), most of which are sufficiently close that the evolution of the two members is expected to be influenced by mass exchange or outright mergers (see Langer, 2012 for a recent review of massive single and binary star evolution). How binary evolution would affect the production of ionising photons, the emission of winds, and the timing and energy of supernovae is a field with a lot of work still ahead of it.
In the early stages of formation, all protostars are accreting gas from their host GMCs via an envelope and a disc. As the gas falls into the potential well of the protostar and is eventually accreted by it, gravitational potential energy is converted to heat, which the protostar radiates away. Although not readily absorbed by the gas, this radiation is absorbed by dust. If the gas density is large enough, thermal coupling of the gas and dust may then transfer heat to the gas, effectively coupling the radiation field to the gas. Offner et al., (2009) point out that accretion luminosity dominates the energy budget of GMCs unless and until O–stars are born.
All photons emitted by all stellar objects transfer momentum, as well as thermal energy, to the surrounding gas and dust. The accretion heating process described above also exerts radiation pressure forces on dust grains, although these are likely to be small and less important than the thermal pressures generated by dust and gas heating. However, radiation pressure from much more luminous massive stars is likely to be dynamically important in very dense clouds (e.g. Krumholz and Matzner, 2009, Murray et al., 2010, Fall et al., 2010).
Although a conceptually simple idea, radiation pressure is difficult to compute in practice. The momentum carried by the photons of a source of luminosity L is L / c, giving (for a point source) a radiative momentum flux at radius r of L / (4π r2 c). However, to compute the radiation pressure, one needs to know how much of this momentum is actually absorbed by the gas. Clearly, if the gas is optically thin, the absorbed momentum can be zero, even if the radiative momentum flux is very large. Krumholz and Matzner, (2009) introduce a parameter ftrap which encapsulates this uncertainty, so that
 |
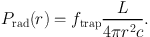(4) |
If ftrap = 1, all the emitted photons are absorbed once before escaping. However, if the shell is moderately optically thick, photons are likely to interact several times, depositing more momentum, before escaping the shell and ftrap exceeds unity. Clearly, computing ftrap self–consistently is a very difficult radiative transfer problem.
As well as thermal feedback, accretion also drives emission of stellar jets – collimated high–velocity outflows emerging bidirectionally along the stellar rotation axis (for a recent view, see Frank et al., 2014). The origin of jets is likely a magneto–hydrodynamic interaction between the star and its accretion disc, producing a magnetic field configuration which acts like a particle accelerator or collimator. The details of this process are still much debated and I will not address them here. From the point of view of view of feedback, it is useful to know that initial jet velocities fall in the range 100 – 1000 km s−1, while material swept up by the jet bowshocks has typical velocities in the range 1–30 km s−1. The mass–loss rate via jets is typically ∼ 10−8 M⊙ yr−1. The shocks produced by jets are highly radiative, so to a good approximation they may be considered as sources of momentum only.