


The previous section concentrated on technical descriptions of algorithms and is intended to be mainly of use to researchers who are considering writing their own feedback prescription and wish to get an overview of how it has been done before. This section is aimed at a different readership and will concentrate on the science results of simulations run using the algorithms and codes described. There will inevitably be a small amount of repetition and overlap between these two sections, so some forbearance on the part of reader is requested.
The first five subsections deal with simulations at GMC scales or below. Figure 4 gives an overview of the mass and size scales covered by a selection of these simulations. The last subsection deals with simulations at galactic scales and above.
5.1. Fragmentation, the IMF, and star formation rates and efficiencies
One of the most urgent questions that simulations involving feedback hope to answer is, what is the effect of stellar feedback on the star formation process itself? At the smallest scales, as modelled by Krumholz et al., (2009), Kuiper et al., (2012b) (discussed in Section 4.1.2) and, in the case of primordial star formation, by Clark et al., (2011) and Smith et al., (2011), feedback affects the rate at which individual stars build up mass by interacting with accretion flows and circumstellar discs, altering their propensity to fragment. At somewhat larger scales, concentrations of dense gas will be disrupted, and heating of the gas will raise the Jeans mass and suppresses fragmentation. However, shocks driven by expanding bubbles and outflows can also locally increase the gas density and cooling rate. Triggered star formation is a very popular topic in observational astronomy, and triggering of star formation by stellar feedback is even more intriguing because it should be directly observable in star–forming regions, and gives rise to the attractive idea that star formation may be self–propagating. There is a wealth of observational literature on this topic (see Dale et al., 2015 for a recent survey) and it has recently also started to receive increased attention from modellers.
There are two popular models of triggering – radiation–driven implosion (or cloud–crushing – Sandford et al., 1982, Bertoldi, 1989) and the collect–and–collapse process (Elmegreen and Elmegreen, 1978) – both of which are now amenable to simulation.
5.1.1. Radiation–driven implosion
The RDI or cloud–crushing regards feedback as an external agent which perturbs a stable or quasi–stable equilibrium of some kind. It can thus be very rapid and need not involve large masses of material. Many authors have considered the effects of irradiating objects of only a few to a few tens of solar masses. Such objects are commonly observed around the borders of HII regions, so their evolution is of obvious interest. They are usually modelled as Bonner–Ebert spheres. Unless the radiation is strong enough to ionise the entire BES, it heats a curved layer, thickest at the point closest to the radiation source. The photo–heated material flows away, driving a shock back into the cloud, a phenomenon known as the rocket effect. It is this which may drive the BES to gravitational collapse.
Gritschneder et al., (2009a), Bisbas et al., (2009), Bisbas et al., (2011) and later Ngoumou et al., (2015) all employed SPH simulations and present similar results. Bisbas et al., (2011) performed a parameter study in which they varied the mass of the BES and the ionising flux. Low fluxes lead to slow but efficient star formation. Higher fluxes produce faster evolution but less efficient production of stars, with star formation concentrated in a pillar–like structure behind the ionisation front. This structure is formed by a shock–focussing phenomenon originating in the curved outer surface of the BEF. For large fluxes or low BES masses, the cloud is destroyed by photoevaporation before any stars form.
Mackey and Lim, (2010) illuminated groups of triaxial clumps and found that small groups of sufficiently massive and dense clumps produced long–lived elongated structures. Three nearly collinear clumps or three clumps close together in a triangular configuration were particularly successful in forming pillars by the smearing of the clumps away from the ionising source and the filling up of shadowed regions behind the clumps with low–density material.
Other authors have instead turned to irradiating turbulent clouds or boxes. Gritschneder et al., (2009b) and Gritschneder et al., (2010) created a turbulent box which they illuminated with plane–parallel radiation from the negative x–direction. The inhomogenous density field allowed the radiation to penetrate to different depths at different locations, producing an irregularly–shaped mass of hot gas which then expanded in the face of the ram–pressure of the remaining turbulent cold gas. The subsequent evolution was found to depend strongly on the Mach number of the initial turbulence. Low Mach numbers presented little resistance to the HII region, which expanded like a piston, producing a rather flat ionisation front. Higher Mach numbers allowed progressively longer and more prominent pillar structures to project into the ionised gas. In the tips of several of these objects, collapsing cores and discs were found, although the simulations could not be run far enough to follow their evolution.
In a series of papers, Tremblin et al., (2012b), Tremblin et al., (2012a) and Tremblin et al., (2013) thoroughly examine the irradiation of perturbed ionisation fronts and turbulent boxes with a view to understanding pillar formation. They begin by imposing on an ionisation front a single sine–shaped perturbation of the same length, but different widths perpendicular to the radiation field to study the influence of the curvature induced in the photoevaporative shock. Narrower perturbations result in longer pillar structures, with shock curvature concentrating material along the pillar axis, while a concave pit is excavated around the base of the pillar. They next reintroduce a flat ionisation front but with a spherical overdensity just behind it. Shock curvature around the obstacle causes material to meet behind it, forming a pillar structure which was observed to be longer the higher the density contrast. Unlike in the case of the perturbed fronts, the pillars produced by this process develop pronounced heads shaped roughly like umbrellas.
In the second paper, a turbulent velocity field with mean Mach number 1, 2 or 4 is irradiated. In common with Gritschneder et al., (2009b), they observe that the higher Mach number turbulence is better able to resist the compression by the hot ionised gas, and the formation of pillar structures. The pillars have much more complex shapes than those formed in the previous paper. In the high Mach number simulation, they also observe globules of dense cold gas isolated inside the ionised gas, which are thrown there by the ram pressure of the turbulence. They also observe a characteristic double–peaked structure in the gas column–density PDF, with one peak corresponding to the turbulent velocity field, and the second to gas compressed by feedback. In the third paper, they show that just such PDFs are observed in the neighbourhood of the Pillars of Creation in M16.
Haworth and Harries, (2012), Haworth et al., (2012) and Haworth et al., (2013) examine the subject of triggered star formation in bright–rimmed clouds (BRCs) using the torus hybrid AMR/Monte Carlo RT code. Their detailed treatment of the RT problem allows them to include several physical mechanisms that have been left out of previous studies, such as the effect of the diffuse ionising radiation field, and to produce synthetic observational images on–the–fly, rather than through post–processing. They find that the diffuse field alters the character of the RDI, particular in cases where the radiation field is of moderate strength, where the diffuse field compresses the target clump very effectively from the sides, resulting in a much denser and more bullet–shaped configuration, as shown in Figure 5. They relate these results to the BRC classification scheme proposed by Sugitani et al., (1991), where gently–curved rims are classified as type A, tightly–curved as Type B and cometary as Type C. High and low radiation fields both produce Type A BRCs, but the strong lateral compression in medium–flux cases reliably leads to Type B or C morphology, as shown in Figure 5. Using standard observational techniques on their synthetic datacubes, they find that the dynamical states of BRCs can be reasonably well recovered, although the synthetic observations systematically underestimate electron densities due to line of sight contamination. This would lead to systematic underestimation of the pressure in the ionised flows, and hence to underestimation of the degree of shock compression and of the effectiveness of the RDI in real objects. The interpretation of molecular line profiles originating in the cold gas is more complex. They are able to reproduce line profiles similar to those observed, but find that some interpretations of those profiles are likely to be erroneous, in particular the two–component envelope–expansion–with–core–collapse model invoked to explain the lack of blue asymmetry (which would imply infall), lack of any asymmetry, or even red asymmetry (implying expansion or outflow) often seen in optically–thick self–absorbed lines in BRCs. Haworth et al., (2013) rule out the EECC model because the material moving towards the observer is ionised and not molecular.
 |
Figure 5. Comparisons of the end result of the medium–flux radiation–driven implosion simulations from Haworth et al., (2012). The left panel shows the result of a monochromatic direct radiation field with the diffuse field treated using the OTS approximation. The middle panel shows the result of using a polychromatic radiation radiation field and again employing the OTS approximation. The right panel depicts the effect of the polychromatic radiation field with the diffuse field calculated self–consistently. |
Moving to larger scales, Dale et al., (2007b) considered the influence of an O–star on a nearly 104 M⊙ turbulent molecular cloud. They used a globally unbound SPH model GMC whose star formation rate and efficiency were expected to be low. By comparison with a control simulation, the Lagrangian nature of SPH allowed them to show that some of the stellar objects formed in the feedback simulation did not form in the control simulation, but the enhancement in star formation rate and efficiency was modest, at 30–40% over ≈ 0.3 cloud freefall times. The also found that some objects which did form in the control simulation were destroyed, aborted or suffered reduced growth due to the ionisation of some of the potentially star–forming material.
Dale and Bonnell, (2012) performed a similar calculation, except that they irradiated a bound GMC. they found that the impact of feedback was even more underwhelming. Although some of the low–density material on the outskirts of the cloud was destroyed, and some intermediate–density gas was driven towards the cloud centre by the rocket effect, the dense core of the GMC where most of the star formation was taking place remained largely unaffected. The number and total mass of stars were little changed and the stellar mass functions proved to be statistically indistinguishable.
5.1.2. The collect–and–collapse process
In contrast to the RDI model, the collect–and–collapse process is driven internally by stars that have formed inside a given cloud and is a large–scale process taking place on relatively long timescales, since it takes time for a sufficient mass of gas to be swept up and to become unstable. The mass of gas required is also generally large enough to form many stars.
Dale et al., (2007a) used calculations of an HII region expanding in a uniform medium to test a theoretical model of the collect–and–collapse process derived by Whitworth et al., (1994) from a perturbation–theory analysis of the gravitational stability of a shocked gas shell. They obtained reasonably good agreement with the model in terms of the time– and length–scales at which the shell became unstable, and of the mass of the fragments produced, and also showed that the results were immune to noise of a factors of a few in the initial density field. They found fragment masses in the range 10–100 M⊙ but were not able to follow the simulations long enough for many fragments to collapse.
A similar approach was taken by Walch et al., (2013) who instead controlled the quantity of structure in their initial density field by constructing fractal clouds with fractal dimensions in the range 2.2 (highly–substructured) to 2.8 (rather smooth). Clouds with small fractal dimensions (corresponding to large–scale structure) resulted in semi–coherent shell structures punctured by large holes through which ionised gas was able to vent (the authors refer to these calculations as shell–dominated). Large fractal dimensions, which generate small–scale substructure, instead resulted in large numbers of pillarlike–objects pointing towards the ionising source, created by dense clumps of material shielding or shadowing gas behind them from the ionising photons (these calculations are hence referred to as pillar–dominated). The fractal dimension had a concomitant effect on the fragmentation induced, with low fractal dimensions leading to a small number of large fragments and large fractal dimensions producing many small objects. The subsequent evolution of the clumps masses is governed by a competition between destruction of the clumps by photoevaporation, and their acceleration away from the ionising source by the rocket effect. Very strong differences in the clump mass functions result, with the mass function slope being -0.18 for a D = 2.0 cloud and -0.91 for a D = 2.8 cloud. Regarding the stars that form, those in the low–D clouds tend to acquire high radial velocities from the acceleration of the large coherent clumps in these runs by the rocket effect, so they tend to be found ahead of the ionisation front. Conversely in the high–D clouds, the stars are usually found at the tips of pillars and are left behind in the HII region.
Ntormousi et al., (2011) examined a similar process, but acting at still larger scales. They modelled the energy and momentum injection by winds of two star clusters 500 pc apart in initially uniform or initially turbulent boxes containing 8000 K atomic gas. Their intention was to study the formation of molecular material, rather than assuming its preexistence, with the transition from atomic to molecular gas handled by piecewise heating/cooling functions. The expansion of the ∼ 108 K wind bubbles drove shocked shells into the warm gas which were simultaneously susceptible to the non–linear thin shell, thermal, and Kelvin–Helmholtz instabilities, generating very complex structure. The former two instabilities combined to form cold overdense clumps in the shells which accounted for 85% of the total mass by the end of the simulations after ≈ 7 Myr. However, the total numbers of clumps was large, so their individual masses were equivalent to moderately massive stars. The calculations were rather similar except that additional inhomogenieties in the background density field created by turbulence induced the two shells to fragment at different times, by approximately 2 Myr. The non–uniform emergence of the NTSI also produced larger shear and amplified the KH instability, leading to longer filamentary structures in this calculation. Filamentary structures were also generated by shear when the two shells collided, resulting a turbulent layer in which the ISM phases mixed and interacted.
5.1.3. Collapsing turbulent clouds
Much recent work has concentrated on implementing feedback of one kind or another as additional physics in simulations of collapsing turbulent clouds. These simulations do not fit neatly into the categories of collect–and–collapse or RDI, although both processes may be taking place within them at different times and places. However, most of these simulations find that the global effect of feedback on these objects is to reduce the star formation rates and efficiencies.
Bate, (2009) use the FLD scheme of Whitehouse et al., (2005) to model the influence of accretion feedback in a 50 M⊙ turbulent cloud. Heating strongly suppresses the formation of new objects after about one freefall time, mostly by preventing disc fragmentation. This reduces the numbers of stars formed by a factor of ≈ 4 compared to a purely barotropic calculation. The decrease in disc fragmentation also results in fewer dynamical interactions, sharply decreasing the numbers of brown dwarfs formed. More importantly, the accretion feedback decouples the mean stellar mass from the cloud initial Jeans mass. These calculations were extended by Bate, (2014) to a 500 M⊙ cloud to obtain improved statistics. The IMFs produced are statistically indistinguishable from the Chabrier IMF, and this result is robust against variations of factors of 300 in the gas metallicity.
This problem was approached in the orion code by Offner et al., (2009) using the FLD implementation described by Krumholz et al., (2007a). Protostellar heating again comes to dominate by about one freefall time in the radiation transfer calculation. The regions heated by the protostars are small, of order 0.05 pc in radius, and fragmentation in most of the cloud proceeds unaffected. The main effect of the feedback is on accretion onto the protostars and on their discs. Warmer discs are able to transfer material onto their central stars at higher rates, so can absorb larger quantities of infalling gas without becoming unstable and fragmenting. They point out that radiation emitted from the protostellar surface originating from, e.g., deuterium burning or Kelvin–Helmholtz contraction, is an essential component of feedback in simulations of this kind, and that simulations such as those by Bate, (2009) which neglect it are likely to underestimate the effects of feedback in fragmentation.
Krumholz et al., (2010) use the orion code to investigate how clouds of the same mass, virial ratio and internal structure but with different surface densities respond to radiative feedback from accreting protostars. They find that low surface density (0.1 g cm−2) clouds analogous to Taurus fragment into a large number of stars of roughly equal masses, whereas clouds with surface densities 1 to 10 g cm−2 fragment very little and most of the mass ends up in either a single massive binary or a single massive star. The root cause is that the higher density clouds support higher accretion rates and therefore higher accretion luminosities, and are also more optically thick so absorb the energy released more efficiently. This has the net effect of raising the Jeans mass over substantial fractions of the cloud volume, suppressing further fragmentation.
Krumholz et al., (2011) modelled feedback from protostars in a massive (103 M⊙), dense (1g cm−2) core using the prescription from Offner et al., (2009), which includes both the energy released by Kelvin–Helmholtz contraction and from deuterium burning. By direct comparison with an isothermal calculation, they found that feedback left the stellar mass largely unchanged, but led to a smaller number of stars forming. In fact, the warming of the gas eventually shut down fragmentation entirely, while allowing accretion onto already–existing stars to continue, resulting in the peak of the mass function moving continuously to higher masses. They attribute this to the high density of their clump, which allows regions heated by different protostars to overlap, so that virtually all the gas in the clump becomes warm, and none of it is able to fragment.
In a subsequent calculation, Krumholz et al., (2012) tried to remedy this problem in two ways. Firstly, they included outflows in addition to thermal feedback. However, this had relatively little impact, reducing star formation rates by around 20 percent, entraining very little material and having no major influence on the cloud structure. However, they also compared different initial conditions. The earlier calculations were initialised with smooth spherical gas distributions seeded with turbulence. Additionally, they constructed initial conditions from fully developed turbulence created in a periodic box with no gravity. This produces a density and velocity field which are initially self–consistent, leading to more distributed star formation and a slower overall star formation rate, since the cloud does not immediately begin to collapse. They found that this lower star formation rate alleviated the overheating issue, leading to a consistent mass function at all times. From this study, they conclude that two apparently only weakly connected characteristics – the star formation rate and the shape of the mass function – become intimately coupled by the inclusion of feedback, and that the latter cannot be correct if the former is too high.
Federrath et al., (2014) model the influence of outflow feedback on 500 M⊙ turbulent magnetised clumps with virial parameters α = 0.4. They evolve the clumps for almost two freefall times, with a control run used for comparison. The feedback simulation forms twice as many sink particles and its star formation efficiency reaches 75%, whereas that in the control simulation reaches 100%, and the difference in the SFEs is larger at earlier epochs, being over a factor of two at one freefall time. On average, the star formation rate per freefall time was 0.57 and 0.30 in the control and feedback runs. About 40% of the stellar mass in the feedback run was accreted, ejected and re–accreted at least once. The average stellar mass is reduced by a factor of ≈ 3 by the combined effect of outflows causing more stars to form, and reducing the accretion rates onto individual objects.
Most simulations of accretion–driven feedback assume that accretion is smooth or continuous. Building on several observational studies suggesting otherwise (e.g. Hartmann and Kenyon, 1996), Stamatellos et al., (2011) and Stamatellos et al., (2012) examine the influence of episodic accretion on the fragmentation of circumstellar discs. The effects of the energy released by accretion are computed using the radiation transport method of Stamatellos et al., (2007), but the accretion rate is determined using a more sophisticated method than in other studies. They divide the accretion discs into two zones – an outer zone, which they can resolve and in which angular momentum transport occurs primarily through gravitationally–driven spiral wave formation, and inner disc which they do not resolve but instead parameterise, where angular momentum transport is driven by the magneto–rotational instability (MRI). The MRI can only operate, however, if the inner disc becomes hot enough to generate the ionisation required to couple it to the protostellar magnetic field. The authors show that the ability of the disc to fragment and form secondary stars or brown dwarfs is determined by two factors. The first is the ‘base rate' of accretion through the inner disc when it is not experiencing an outburst. This sets the temperature to which the disc (very quickly) relaxes when an accretion outburst is complete. The second factor is the duration of the intervals between outbursts, which determines whether the disc has time to become gravitationally unstable between stabilising accretion outbursts. If the intervals are sufficiently long and the disc is able to cool to low enough inter–burst temperatures, they find that accretion feedback is much less effective in suppressing disc fragmentation than inferred by, for example, Bate, (2009). Vázquez-Semadeni et al., (2010) use the art code (Kravtsov et al., 1997) with energetic feedback from O–stars implemented by the deposition of energy in single grid cells where star particles are located, with energy deposition rates adjusted to obtain HII regions of reasonable sizes, temperatures and internal velocity dispersions. They simulate the formation of a flattened configuration of molecular gas from two colliding streams. Feedback increases the mass of dense material while decreasing the star formation efficiency, by factors up to ≈ 10. Feedback is unable to destroy the clouds themselves, nor the atomic streams from which they are forming, but it is able to destroy the smaller–scale dense clumps where star formation is actually occurring. The HII regions do produce more dense clumps, but these generally disperse and fail to form stars of their own.
The effects of photionizing feedback on embedded clusters formed in artificially–constructed turbulent clouds was examined by Dale et al., (2012a) and Dale et al., (2013a). They found that star formation rates and efficiencies were reduced by factors of up to two by the disruption of the dense filaments of gas feeding the clusters. Feedback was largely unable to unbind the clusters themselves though and had little effect on the stellar mass functions. They were able to demonstrate, by comparison with control simulations, the triggering of stars in the sense of the formation of stars that would not otherwise have been born. However, they found that the triggered objects were spatially and dynamically mixed with the spontaneously–formed objects and were therefore very difficult to identify.
Many simulations of turbulent clouds still rely on simple equations of state or optically thin heating and cooling functions to compute the background gas temperature, when in fact this is likely to be set by the external bath of radiation and cosmic rays in which the clouds sit, and by the complex chemistry driven thereby. Several papers make use of the treecol (Clark et al., 2012a) algorithm to compute the optical depth from the outside of the cloud to any point in its interior, and therefore the heating rate from the external radiation field. Glover and Clark, (2012b) used the combination of treecol and the chemical network of Glover and Mac Low, (2007) and Glover and Clark, (2012a) to evaluate the importance of molecular cooling on star formation. They showed that in fact cooling from C+ and dust were sufficient to allow star formation to proceed, once sufficiently dense gas is formed. They stress that this does not mean that molecular cooling is irrelevant, but that it is not necessary.
Clark et al., (2012b) use similar numerics to answer the question of how long an observable molecular cloud takes to form. They model colliding atomic flows at either 6.8 or 13.6 km s−1. They find that molecular hydrogen appears early on, respectively 10 and 3Myr before the onset of star formation, so that the clouds are in this respect ‘molecular' long before they begin manufacturing stars. However, detectable amounts of CO form much later, about 1–2 Myr before star formation commences, supporting the idea that there could exist a population of undetectable molecular clouds. Smith et al., (2014) extended this work to galactic–disc scale simulations using arepo and showed that 42% of the molecular mass in their model spiral galaxy was in CO–dark form.
Clark and Glover, (2014) examine the question of whether there is a column–density threshold for star formation, as suggested by, e.g. Schaye, (2004) and Lada et al., (2010) (who find a value of 116 M⊙ pc−2). They find that the correlation between column– and volume–density in their model clouds is very poor, so that the latter cannot be safely inferred from the former, and the star formation rate in volumetrically–dense gas is much higher than the star formation rate in gas at high column densities. They do infer that there is a minimum mean column below which molecular clouds are sterile, but is roughly one order of magnitude lower than the threshold discussed by Lada et al., (2010).
5.1.4. Star formation from reinserted gas
Under certain circumstances, the matter injected into star clusters by the combined winds and supernovae of their massive stars can itself become the raw material for a subsequent round of star formation. This is a particularly intriguing idea, given that many globular clusters are observed to have multiple main sequences.
Two–dimensional simulations of super star cluster winds were performed by Wünsch et al., (2008) using the zeus code. Matter and energy are inserted at the centre of a spherical grid. Above a threshold value for the mass injection rate and mechanical luminosity, the cluster winds transition from a smooth outflowing state to one in which the matter inside a critical stagnation radius is subject to thermal instability. Clumps of gas inside the stagnation radius cool catastrophically and collapse under the thermal pressure of the surrounding wind. Most of the collapsing clumps are trapped inside the cluster volume and are obvious candidates for forming a second generation of stars.
5.2. Gas expulsion and cloud destruction
A long–standing problem in star formation is explaining why it is such a slow and/or inefficient process. The Galaxy's molecular clouds cannot be forming stars on their freefall timescales, because this would result in a Galactic star formation rate about two orders of magnitude higher than is observed, and would have left the Milky Way devoid of gas to form stars out of several Gyr ago. Stellar feedback has long been called upon to solve this problem, by slowing the collapse of GMCs, or destroying them before they are able to convert more than a few percent of their gas to stars.
Analytical work by, e.g., Matzner, (2002) indicates that expanding HII regions are likely to be the main source of energy on GMC scales, at least until the detonation of the first SNe. Dale et al., (2005) simulated the impact of the HII region driven by a single very massive star into a non–turbulent cloud. Gravitational collapse gave the cloud a filamentary structure, with the filaments meeting at a common hub at the centre of mass, where the massive star was to be found. The dense filaments strongly retarded the growth of the HII region, partly due to the deposition of neutral gas into the HII region, causing it to collapse and regrow, or flicker. Also, as in the simulations by Gritschneder et al., (2010), the ram pressure of the flows resisted the expansion of the ionised gas in many directions. Much of the ionised gas escaped from the region near the radiation source through moderately collimated outflows. Although sufficient kinetic energy was nominally deposited by ionisation to unbind the cloud, much of it escaped through the outflows and collapse continued largely unimpeded.
In a series of papers, Dale and Bonnell, (2011), Dale and Bonnell, (2012) and Dale et al., (2013b) investigated the ability of photoionisation to disrupt instead turbulent GMCs with a range of initial radii, masses and turbulent velocity dispersions. The clouds were allowed to form a small number of O–stars, or subclusters large enough to host O–stars. The effects of feedback varied strongly with cloud properties, in particular with the escape velocity. GMCs in the Milky Way all have very similar column densities, i.e. MGMC ∝ RGMC2. Since the escape velocity vESC ∝ (MGMC / RGMC)1/2, it follows that vESC ∝ MGMC1/4. This is weak scaling, but the escape velocities of Milky Way clouds lie in the range 1– 10 km s−1, which is significant because the speed of sound inside an HII region at around solar metallicity is fixed at ≈ 10 km s−1. Dale et al., (2013b) showed using a very simple model that this leads to a very steep relation between the mass of a cloud and the fraction of material that can be unbound by HII regions in the period before supernova detonation.
Other authors have investigated the effects of feedback on different geometries. Ionisation feedback form massive stars forming inside a rotating 103 M⊙ clump is studied by Peters et al., (2010). The clump contracts to a disc–like structure with massive objects forming at the centre. As the simulation progresses, the formation of smaller objects further out in the disc starves the massive objects of gas. This in turn allows HII regions to grow, preferentially out of the disc plane, although what accretion continues causes them to fluctuate and flicker. They propose that this behaviour may explain the well–known ultra compact HII region problem, and find that all the HII region morphologies catalogued by Wood and Churchwell, (1989) appear naturally in their simulations.
Colín et al., (2013) simulate the formation of molecular clouds and clusters in colliding flows of warm neutral gas, and follow the effects of feedback from the cluster stars. The clouds formed by their colliding streams are flattened, turbulent, and have masses of order 104 M⊙. Ionising feedback is effective at bringing star formation to a halt at star formation efficiencies of around ten percent, in contrast to the simulations of Dale et al., (2012b), who found that even the lowest–mass clouds were able to continue forming stars, albeit slowly, under the influence of ionisation. Colín et al., (2013) suggest that the reason for the discrepancy may be that their clouds, being flattened, are less gravitationally bound than those of Dale et al., (2012b), and thus easier for feedback to disperse. The fractal clouds modelled by Walch et al., (2012) are also readily destroyed by photoionisation on timescales of 1–2 Myr, despite a very inefficient uptake efficiency of kinetic energy of well under 1 percent. Since these clouds are also spherical, this explanation cannot work here. It is possible that the fact that the O–stars in Dale et al., (2012b)'s calculations first have to destroy the dense filaments and accretion flows in which they born impedes them in disrupting the clouds. It is also possible, as suggested by Tremblin et al., (2012a), that the turbulence initially present in the cold gas in Dale et al., (2012b) (but not in those of Walch et al., 2012) plays a role.
While winds are generally regarded as being subordinate to HII regions, they still inject significant quantities of energy into clouds and, in very dense gas, are more efficient at gas dispersal. SPH simulations by Dale and Bonnell, (2008) and Dale et al., (2013c) modelled momentum input from O–star winds on turbulent model clouds. As with ionisation, they found that the impact of the winds depended strongly on the escape velocity of the clouds, despite there being no obvious limit to the rate at which wind bubbles can expand. Winds were able to slow the star formation rate somewhat by disrupting the accretion flows feeding stellar clusters, and in general spatially separating the stars from the gas.
As well as the damage they themselves do to GMCs, winds and ionisation are important because of the way in which they set the environments in which the eventual supernovae of the massive stars detonate. Pelupessy and Portegies Zwart, (2012) simulate winds and supernova more self–consistently in an SPH simulation by injecting hot gas into embedded clusters modelled as Plummer spheres consisting of 103 stars mixed with 105 SPH gas particles whose mass is set to give various SFEs in the range 0.05–0.5, and with total system masses in the range 700–8000 M⊙. Winds and SNe are introduced adiabatically with feedback efficiencies (i.e. fraction of the emitted stellar energy retained by the gas) of either 0.01 or 0.1. For the higher star formation efficiencies, both feedback models are able to efficiently expel gas from the clusters, the difference being that with efficient coupling, this is achieved by the winds whereas with weak coupling, the supernovae are required to complete the task. Where the SFE is 0.05, the clouds are more resistant to the winds owing to the higher gas masses, but are unable to survive the supernovae. In these runs, the expulsion of the gas also promptly disrupts the clusters.
This problem was tackled in an Eulerian context by Rogers and Pittard, (2013), who modelled the winds (and eventual supernovae) from a trio of massive stars in preformed turbulent clouds. The winds rapidly cleared out the central region near the stars, but hot wind gas streamed out of the cloud through low–density channels, entraining little neutral material, as shown in Figure 6. Much of the coldest densest material was able to survive the winds for several Myr, producing pillar–like structures pointing back towards the O–stars. The supernovae did eventually prove sufficient to destroy the cloud. Similar models using the nirvana code of multiple stellar winds and SNe evolving in a smooth background are discussed by Krause et al., (2013). The energy input from the supernovae is rather unimportant, with that accumulated in the wind bubbles beforehand being much more significant. The evolution of the supernovae does depend on the state of the wind bubble, with larger wind bubbles giving longer cooling times.
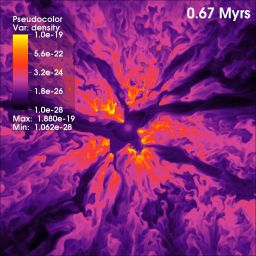 |
 |
 |
| (a) | (b) | (c) |
Figure 6. Time evolution of the stellar wind simulation of Rogers and Pittard, (2013). The images show density slices though the midplane of the simulations 0.67 Myr (left panel), 2.31 Myr (centre panel) and 3.96 Myr (right panel) after the ignition of the wind–driving stars located at the centres of the images. |
||
Walch and Naab, (2014) take the simulations of Walch et al., (2012) further by detonating supernovae inside their fractal clouds, both those which have suffered ionising feedback and those which have not. The clouds' fractal structures distort the expanding shell and allow leakage of hot gas though low–density channels, advecting large quantities of energy away. Particularly in the realistic radiative cooling cases, most of the explosion energy is lost and only a few percent is imparted to the surrounding cloud. In models where the cloud has experienced photoionisation prior to the supernova, the energy uptake by the cloud is more efficient, but only by a factor of ∼ 2, because the lower average density inside the remnant encounters delays the onset of radiative cooling somewhat.
ramses simulations by Iffrig and Hennebelle, (2015) investigate the influence of the SN detonation site (which other workers find to be of crucial importance in galactic–scale simulations – see Section 5.6.2) on a turbulent 104 M⊙ cloud. SNe are modelled as purely thermal energy injected in a region four cells across, and detonated deep inside the cloud, on the cloud border, or outside the cloud. The effect of exploding a supernova outside the cloud was minimal, with only a very small fraction of the explosion momentum being transmitted to the cold dense material. Conversely, the internal explosion deposits roughly half of its momentum in the cloud and unbinds about half the cloud's dense gas.
GMCs exhibit supersonic turbulent velocity fields with characteristic dispersions typically in the range 1–10 km s−1 (e.g. Heyer et al., 2009). The turbulence provides an additional means of support against gravitational collapse and has been incorporated into the very successful gravo–turbulent model of star formation (e.g. Mac Low and Klessen, 2004). However, the cause of these velocity fields is much debated, since supersonic turbulence, even in a magnetised cloud, will die away due to energy dissipation in shocks in about one crossing time (Mac Low et al., 1998). Many authors have suggested that, whatever the original source of the turbulence, it is continuously replenished by feedback.
The combined action of multiple jets has been championed in particular by Matzner, (2007), who showed analytically that momentum injection from jets could maintain turbulence in ∼ 103 M⊙ clumps. Other authors (e.g. Mac Low and Klessen, 2004) note that the rate of turbulent dissipation is comparable to the expected energy injection rate from jets. Nakamura and Li, (2007) confirmed the expectation from Matzner, (2007) that turbulence driven by collimated outflows decays more slowly than that resulting from multiple isotropic motions. This is a consequence of the collimated jets penetrating to greater depths into the surrounding cloud, driving turbulence on large length scales, for which the decay times are longer. They observed that even a modest rate of star formation was able to reproduce a turbulent–like velocity power spectrum with a power–law form Ek ∝ k−2.5 over about one and a half decades in wavenumber. The turbulent velocity field reached a steady state with gravitational collapse.
Carroll et al., (2009) adopted a similar model with 192 randomly–oriented narrow–angle jets inside a periodic box, which they also observed to reach a steady state after a few crossing times. They compared the resulting field explicitly to an artificially–driven isotropic field with a power spectrum of Ek ∝ k−2.5, finding that the jets produced a spectrum with a slightly steeper exponent of about -2.75. Again, the power–law only extended over approximately one decade in k. In these simulations and those of Matzner, (2007), multiple jets rapidly achieve an equilibrium and produce a velocity field resembling turbulence, with a power–law power spectrum over moderate ranges of wave numbers. However, in both cases, periodic boundaries are used, and it is not clear what affect this has on the results. Periodic boundaries make it difficult for injected energy to escape the grid, and makes a steady state a more likely outcome.
Hansen et al., (2012) explicitly examine the driving of turbulence in their simulations of radiative and outflow feedback in low–mass star–forming regions. The action of outflows reverses the decay in the velocity dispersion of the gas but the turbulence driven by the outflows is of a different form to the that with which their clouds were seeded. In fully developed isotropic hydrodynamic turbulence, the ratio of the energy density in solenoidal versus compressive modes is 2, but shear at the edges of their relatively long outflow cavities preferentially drives solenoidal modes, increasing this ratio to values of up to 10. Similar results are reported by Offner and Arce, 2014.
However, not all simulators have arrived at the conclusions that jets are efficient at driving turbulence. Banerjee et al., (2007) modelled in great detail in flash the evolution of a single jet and they concluded that the jet was not able to propagate the supersonic motions required to drive turbulence to large enough distances, nor was it able to entrain sufficient material, for this to be a viable driving mechanism. Jets are in any case not likely to be able to maintain turbulence on GMC scales because their combined filling factors are too low. Several groups have instead looked at the possibility of driving by expanding HII regions, again inspired by analytic calculations (e.g Matzner, 2002, Krumholz et al., 2006) suggesting that expanding photoionised bubbles should be able to supply energy at a high enough rate to compensate for turbulent decay.
Mellema et al., (2006a) simulate the evolution of single HII regions in pre–existing turbulent clouds and find that the velocity dispersion in the neutral gas is not only prevented from decaying but raised to values higher than in the original velocity field. Similar results were obtained by Arthur et al., (2011), who also showed that this result is little affected by the presence of magnetic fields of realistic strength
Walch et al., (2012) in contrast model HII region expansion in fractal clouds with no initial velocities. They subtract the kinetic energy due to the radial expansion of the HIIR and find that the remaining random component, which they equate with turbulence, is driven more strongly by photoionisation than by gravitational collapse, although the efficiency of energy uptake is very low at ≈ 0.05%.
In their simulations of an irradiated turbulent box, Gritschneder et al., (2009b) measure compressive, solenoidal, and total power spectra and compare the simulations including feedback to a control run in which the initial turbulence, which has power–spectrum close to Kolmogorov, is allowed to die away. They find significant driving, particularly of compressional modes, in the cold gas, but more so at smaller spatial scales, resulting in a flatter power spectrum.
Krumholz and Thompson, (2012) and Davis et al., (2014) both find that radiation pressure illuminating an isothermal atmosphere from underneath is able to drive turbulence provided that the radiative flux is large enough to overwhelm gravity in the atmosphere. This leads to rapidly development of the Rayleigh–Taylor instability and the outbreak of turbulence, as discussed in Section 4.1.2.
Starting from the photoionisation calculations of Dale and Bonnell, (2012), Boneberg et al., (2015) used structure functions and power spectra to assess whether the multiple bubbles expanding from different locations were able to replenish otherwise decaying turbulence. The simulations were initially seeded with Burgers turbulence, but the velocity field had transitioned to the Kolmogorov slope by the onset of star formation. They found that, particularly in the lower–mass and smaller clouds, the structure function in the control simulations subsequently became much flatter, with large quantities of power being lost on intermediate scales. By contrast, in the photoionised runs, structure functions closely resembling that expected of developed Kolmogorov turbulence were maintained, or restored, as shown in Figure 7. Feedback also regenerated the characteristic ratio of power in compressive to solenoidal modes of 0.5.
All the work cited in this section so far has concentrated on the study of turbulence in the cold, neutral star–forming gas. Medina et al., (2014) demonstrated the development of turbulence in the ionised gas inside their HII regions. A statistically–turbulent velocity field takes approximately 1.5 crossing times of the HII region to establish itself, but the power spectrum slopes are substantially shallower than would be expected for compressible or incompressible turbulence. They suggest that this is due to the driving of turbulence on all scales, contrary to the classical model where it is driven only on the largest scale.
Many authors modelling feedback on larger scales report producing velocity fields with power spectra resembling turbulence. However, in many cases, feedback is not the only driver of turbulence and it competes with shear in galactic discs, self–gravity and various fluid instabilities, particularly the thermal instability. Some simulations find that the influence of feedback on turbulence diagnostics such as the gas density PDF is minimal (e.g. Wada and Norman, 2007). A prominent model of galactic dynamics simulated by, for example, Ostriker and Shetty, (2011), Kim et al., (2011) and Shetty and Ostriker, (2012), has as one of its main components a vertical equilibrium in the galactic disc between supernova–driven turbulence and turbulent dissipation, which they find is achieved on timescales shorter than a galactic rotation period.
5.4. Effects of different feedback mechanisms combined
Stellar feedback mechanisms obviously do not act alone but in concert and, even if one is likely to dominate, they are nevertheless likely to influence each other to some extent. It is often not obvious how such interactions will proceed and more and more authors are now investigating the combined effects of several mechanisms.
Accretion of material by protostars produces two very different but almost always concurrent feedback mechanisms, namely accretion heating and jets, which affect the star's surroundings in very different ways. Cunningham et al., (2011) simulated the evolution of a 300 M⊙ turbulent core including the effects of stellar jets, and using FLD to follow the radiative cooling of the shocked gas and radiative feedback from accretion and from the protostars themselves. They observe that the outflows reduce the efficacy of radiative feedback by providing low–density channels through which photons can escape.
In common with Krumholz et al., (2012), Hansen et al., (2012) simulate the interaction of radiative protostellar feedback and outflows, using the same model as Cunningham et al., (2011). They simulate a 0.65 pc turbulent box containing 185 M⊙ of material. Simulations including radiation and outflows form substantially more stars than those with radiative feedback alone because the outflows reduce the accretion rates which contribute much of the protostellar luminosity. The dual–feedback simulation in fact results in very similar numbers of stars and total stellar mass to a simulation with outflows and a barotropic equation of state. This result is difficult to reconcile with that of Krumholz et al., (2012), who found that the addition of winds was not able to strongly reduce the protostellar accretion rates or luminosities in their calculation. Krumholz et al., (2012) attribute the ineffectiveness of outflows in their simulation to the higher densities of their clouds (1 g cm−2 as opposed to Hansen et al., 2012's 0.1 g cm −2).
Another complicating factor in the evolution of combined HII regions and wind bubbles is the possibility of the rapid motion of the driving star through its natal cloud. Arthur and Hoare, (2006) and Mackey et al., (2015) study the evolution of wind bubbles inside HII regions driven by runaway stars. The wind bubbles become asymmetrical almost immediately, while the HII regions take much longer to do so, owing to their much lower sound speed. Mackey et al., (2015)'s wind bubbles fill about twenty percent of the HII region volume, appropriate for the relatively low–luminosity star modelled, and have relatively little influence on the champagne–flow–like internal dynamics of the HII region. Arthur and Hoare, (2006) use higher wind momentum fluxes and the winds dominate the flows in their calculations. Mackey et al., (2015) find, as suggested by Rosen et al., (2014), that much of the wind energy is radiated away via microturbulent mixing driven by Kelvin–Helmholtz instabilities at the contact discontinuity between the wind and the HII region. However, they stress that the contact discontinuity is likely modified by numerical diffusion, and that they include neither physical diffusion nor magnetic fields, so urge caution in interpreting this result.
From the point of view of individual massive stars, it is clear that photoionisation and the different kinds of stellar wind expelled during different stellar evolutionary stages will interact in complex ways. Freyer et al., (2003) and Freyer et al., (2006) investigate the coupled evolution of the HII regions and wind bubbles of (respectively) a 60 and a 35 M⊙ star in a uniform background. In the case of the lower–mass object, the effect of the wind is largely to compress the HII region into a thick shell lining the inside of the feedback–blown cavity. By contrast, the stronger wind of the more massive star sweeps up a shell inside the HII region which becomes dense enough to fragment, casting shadows on the ionisation front. This leads to a spikelike structure in the ionised gas, although this does not last very long as the HII region is quickly swept up into a thin shell by the wind.
Toalá and Arthur, (2011) use 1– and 2D RHD models to study the interaction of the fast WR wind with the previously–ejected and slower YSG or RSG wind around 40 and 60 M⊙ stars, comparing two different stellar evolution models. The results depend strongly on the nature of the mass loss in the slower wind phase, on which the two stellar evolution models do not agree. A short RSG phase leads to a thin dense wind shell which becomes strongly unstable and breaks up into clumps when hit by the WR wind, whereas a long RSG/YSG phase leads to a much thicker and lower–density wind which is stable to interaction with the WR wind. Detailed 3D ramses simulations investigate the mutual interaction between the HII region, wind bubble and eventual supernova explosion of a 15 M⊙ star in smooth ambient media at a range of densities. They observe that the expansion of the wind bubble is particularly sensitive to the evolution of the ionising photon flux and wind luminosity of the star as it ages. In the denser media, they find that the wind bubble is prevented from expanding by the pressure in the HII region until the star moves onto the horizontal branch, and that in general winds from the 15 M⊙ object considered do not inject significant energy into the ISM. They also find, in common with Walch and Naab, (2014), that the fact that the supernova expands into a rarefied medium increases its effectiveness by delaying the transition to the radiative phase.
The above already complicated scenarios are made richer still by the likelihood that a massive star will have a close binary companion, often another massive star. Mackey et al., (2014) present a model of the circumstellar material around the red supergiant star Betelgeuse. Since massive stars tend to be found in one anothers' company, the cool wind emanating from a red supergiant is likely to be photoionised by its companions. In the case of a star moving supersonically through the ISM, the wind will be terminated by a bow–shock, leading to a layered structure where a parabola–shaped outer shock encases an ionised wind separated from the supergiant's neutral wind by a spherical neutral shell confined by the ionised wind. The net effect is to confine a large quantity of material (up to about one third of the total wind mass) in a dense shell near the star. This shell becomes important when the star eventually explodes, since the blast wave will promptly collide with the shock, potentially radiating a large fraction of its energy.
From the point of view of the effects feedback on the surrounding ISM, Dale et al., (2014) and Ngoumou et al., (2015) studied, at very different scales, the combined effects of photoionisation and momentum–driven winds. Dale et al., (2014) essentially repeated the simulations of Dale et al., (2012b) and Dale et al., (2013b) with the inclusion of stellar winds, having already established in Dale et al., (2013c) that winds acting on their own were not a very effective means of dispersing any of their model clouds. The results of their simulations were in fact little different from the photoionisation–only simulations, as shown in Figure 8. At very early stages, the winds helped to clear away the dense filamentary gas in which the O–stars in these calculations are born, but the structure of the cold gas rapidly comes to be dominated by the effects of the expanding HII regions. The structures of the HII regions themselves were observed to be different, since the winds expel much of the ionised gas through low–density channels, excavating large holes inside the HII regions and leaving the ionised gas as a thin skin lining the inside of the shocked bubbles of cold gas in a fashion reminiscent of the simulations of Freyer et al., (2006).
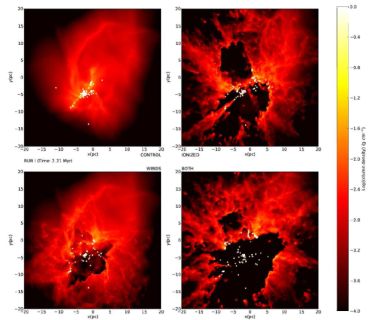 |
Figure 8. Comparison of the control (top left), ionisation–only (top right), winds–only (bottom left) and dual–feedback (bottom right) Run I calculation from Dale et al., (2014). Colours represent gas column density and white dots are sink particles used to model stars. Screenshots are from an epoch 2.2 Myr after the time at which feedback is enabled. While the winds do have some effect on the cloud, that of the HII regions is much more severe. This is even more true of other simulations in Dale et al., (2014). |
Ngoumou et al., (2015) instead modelled the effect of including winds in the radiation–driven implosion models of Bisbas et al., (2011). They also observed that, while there are some visible impacts on the morphology of the ionised gas, the cold gas is almost entirely insulated from the winds by the HII region.
Peters et al., (2014)'s flash simulations include radiative heating from ionising and non–ionising photons, and from jets. They start from the same initial state as Peters et al., (2010) and the collective outflow driven by the stars, being directed along their rotation axes, act perpendicularly to the disc, rapidly exiting the simulation box. The leading fronts of the outflow cones are Rayleigh–Taylor unstable, exhibiting elongated fingers, and the mass and momentum contained in the outflow are substantially larger than those driven by the HII regions. They find in fact that only jets are able to reproduce observed levels of mass and momentum entrainment in outflows in their simulations.
5.5. Combining feedback and magnetic fields
The role of magnetic fields in ISM evolution remains unclear, partly due to the difficulty of measuring their strengths and geometries. Nevertheless, the typical flux densities present in molecular clouds are known to order–of–magnitude accuracy, sufficient for their effects to be meaningfully simulated. This is not the place to discuss their general effects, but it is clear that jets and bubbles will interact with magnetic fields, and some authors have begun to explore this issue.
Krumholz et al., (2007b) considered the effect of a uniform magnetic field on HII region expansion. They model the case where the initial gas density and magnetic field strength are such that the thermal sound speed in the promptly–ionised gas is much larger than the Alfvén speed vA in the undisturbed neutral gas, and vA is much greater than the thermal sound speed in the neutral gas. At early times, the effect of the magnetic field is minimal, but it becomes significant when the magnetic pressure inside the swept–up shell becomes comparable to the thermal pressure inside the HII region, which occurs when the shell expansion velocity drops to near vA. They define a critical radius rm at which this occurs, give by rm = (cII / vA)4/3 Rs. From this point on, the HII region and the shell are deformed from the usual spherical shape. Gas motions along the field lines are unaffected, so that the expansion in these directions continues in a similar way to that in a normal HII region. Perpendicular to the field, expansion is resisted and the shell is initially supported by magnetic pressure. However, as the expansion proceeds, the field lines deform to become perpendicular to the shell surface, so the shell loses magnetic support and becomes thinner. Very similar results were obtained by Wise and Abel, (2011) in testing their RMHD implementation in enzo, and by Mackey and Lim, (2011).
Gendelev and Krumholz, (2012) build on the work of Krumholz et al., (2007b) by considering also blister HII regions. The orientation of the magnetic field, not surprisingly, strongly affects the results, in particular the degree to which the magnetic field lines are distorted and the distribution of the gas kinetic energy in the swept–up shock. In particular, orienting the field parallel to the edge of the cloud results in the strongest compression of field lines, and in almost all the shell kinetic energy being stored around the lip of the depression in the neutral gas. In all runs, they observe that the gas kinetic energy is smaller than in the case with no magnetic fields, but that the total energy is much larger, owing to energy stored in the magnetic fields. They propose that this could be an effective driver of turbulence.
Peters et al., (2011) present an extension to the simulations of Peters et al., (2010) in which they combine HII region expansion and magnetic fields in simulations of a 103 M⊙ rotating cloud. The cloud is initially threaded with a uniform magnetic field parallel to its rotation axis, with a mass–to–flux ratio fourteen times larger than that required to support it, consistent with observed field strengths. As expected, while the field cannot prevent gravitational collapse, it slows it, reducing the global star formation rate in the calculations by a factor of order unity. However, the most massive star, which forms at the centre of the disc, acquires a larger mass because magnetic braking drains the region of angular momentum, enhancing infall into the centre. As in their earlier calculations, the central regions of the cloud collapse into a flattened rotating disc–like structure, with the rotation and collapse dragging the magnetic field into a toroidal configuration. Once a sufficiently massive star has formed to drive an HII region, the influence of the magnetic field is largely to slow the HII region's expansion.
Arthur et al., (2011) in contrast examined the effects of magnetic fields on HII regions expanding in already–turbulent clouds. They simulate a 4pc magnetised turbulent box in which the mean atomic number density is 1000 cm−3 and the ratio of thermal to magnetic pressure is 0.032. Into the centre of the box, they place either an O9 or a B0.5 star, whose ionising photon fluxes differ by 2.5 orders of magnitude. In the case of the brighter star, their box size is smaller than the critical radius defined by Krumholz et al., (2007b) at which the HII region expansion should start to feel the influence of the magnetic field. However, in the case of the fainter star, whether or not this is true depends on whether the RMS or mean magnetic field strength is used to compute the representative Alfvén speed in the neutral gas. They find that, in the former case and as expected, the presence of the magnetic field has little effect on the gas morphology produced by the HII region expansion, aside from some smoothing out of small–scale structures. In the B–star simulation, they find that the magnetic field does become critical during the simulation, but that it still fails to have a marked effect on the gas structure. They attribute this result to the disordered state of the field, which has no preferred direction except on small scales, and cannot therefore deform the HII region in a systematic or global fashion. In fact, because the pressure in the HII region exceeds the magnetic pressure for most of the duration of the simulations, the HII region expansion deforms the magnetic field into a more ordered configuration, with field lines approximately parallel to the ionisation fronts.
Mackey et al., (2013) consider the influence of magnetic fields on the HII regions driven by runaway O–stars (using ζ–Oph as an example). As in other studies, HII region expansion and the accumulation of dense material perpendicular to the field lines are strongly retarded. The opening angle of the cone trailed by the star is increased by the presence of the magnetic field.
The interaction of supernovae and magnetic fields in turbulent 104 M⊙ clouds is investigated by Iffrig and Hennebelle, (2015), who find that the magnetic field has only a rather weak effect, modestly increasing the efficiency of momentum coupling between the supernova and the cold gas in the case where the explosion occurs deep inside the cloud.
Some of the clearest signs of the action of feedback in real astrophysical systems are the production of unusual structure, such as pillars. If these are to be correctly interpreted, the role of magnetic fields in their formation and evolution must be understood. Henney et al., (2009) conduct RMHD simulations of the formation and evolution of pillars using the C2–RAY algorithm. Spherical globules with Gaussian density profiles are embedded in an initially uniform magnetic field aligned at a given angle to the x–axis, along which lies a point source of ionising photons. With magnetic pressures of order 100 times the initial gas pressure, the effects on the evolution of the system are profound and depend strongly on the orientation of the field relative to the direction of the source. When the field is perpendicular, the globule evolves to a flattened structure, whereas a 45 degree angle results in a very asymmetric globule which the authors describe as comma–shaped. Thin–shell instabilities caused by rocket acceleration cause the heads of the pillars to fragment into smaller objects. Similar results are obtained by Mackey and Lim, (2011) (an example is shown in 9), who also observe that radiation–driven implosion and rocket acceleration both tend to align the magnetic field with the radiation field. The morphologies in the simulations can be used indirectly to constrain the field strengths in real objects, such as the famous M16 pillars. High field strengths produce sheet and ribbonlike structures which should be easily observable, but are not seen in M16. Emission in that region is instead consistent with that seen in the simulations where the accretion flow from the pillar head is roughly spherically symmetric.
 |
Figure 9. Projections along the z–axis (left) and y–axis (right) of RMHD pillar simulations from Mackey and Lim, (2011) at 100 (top) 250 (middle) and 400 (bottom) kyr. The magnetic field is aligned with the z–axis. The images are rendered in energy flux in recombination line radiation, arbitrarily normalised. |
Regardless of their direct interaction with a given feedback mechanism, magnetic fields will always influence to some extent the environment in which feedback operates. This issue is explored by Price and Bate, (2009), who extend the work of Bate, (2009) by repeating their calculations with magnetic fields of various strengths included. They find that magnetic fields and thermal accretion feedback (which do not interact directly) are additive, in the sense that they act at different scales. The magnetic fields, if they are strong enough, affect the large–scale collapse or contraction of the cloud, exerting an influence on gas of all densities. Accretion feedback, by contrast, only operates on the smallest scales by suppressing fragmentation in the densest material. The average stellar mass formed in their calculations is lower than in pure hydrodynamic calculations.
When considering feedback from jets, however, the interaction with the magnetic field is more direct. Wang et al., (2010) model the effect of jets on magnetised clouds, where the jet emission is aligned with the local field direction. Magnetic fields on their own do not much influence the denser material from which their sink particles are accreting, but the inclusion of outflows partially disrupts the dense gas and slows accretion substantially. Combining the two process increases this effect, since the magnetic fields couple gas over much large distances than local pressure forces are able to, reducing total mass accretion rates and those onto individual stars by around an order of magnitude.
Myers et al., (2014) perform simulations of the formation of a star cluster including radiative and outflow feedback from protostars, and magnetic fields. Contrary to Price and Bate, (2009), they find that their mean stellar mass increases. They interpret this as being due to the mechanism which actually terminates accretion in many cases in the Price and Bate, (2009) simulations, which is the ejection of sink particles from the densest gas by N–body interactions with other sinks, in a globally contracting cloud. This shuts off accretion onto the sink and fixes its final mass. Myers et al., (2014) do not simulate a globally–infalling system, and most of their sinks form from fragmentation. As well as slowing the star formation rate by factors of around two, the magnetic fields also suppress fragmentation, decreasing the numbers of sinks and raising the average fragment mass.
In larger–scale simulations, the star formation process itself usually cannot be directly resolved, certainly in terms of individual stars. It is often modelled by assuming that all the gas above some threshold density generates stars with some efficiency on some timescale, which is often taken to be the freefall time at the threshold density, i.e.
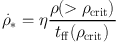 |
(45) |
With this prescription, the star formation rate automatically reproduces something close to the Schmidt–Kennicutt (SK) law. Some simulations do not impose such a law but try to recover it. The SK law is the result of regulation of star formation. What is the regulator is unclear, but clearly little can be said about the role of feedback if the SK law is imposed from the outset. However, large–scale simulations have other goals, such as reproducing the multiphase ISM and driving turbulence, and reproducing the structure of galaxies, especially spirals.
5.6.1. Vertical slices or columns through a disc and shearing boxes
Here, simulators model a vertical slice or column through a galactic disc, often including tidal and Coriolis forces as external perturbations. These simulations are generally most concerned with the dynamical equilibrium between the vertical gravitational field and the thermal and dynamic pressure on the gas.
The effects of expanding HII regions on galactic disc scales are explored by Koyama and Ostriker, (2009). They produce a turbulent, multiphase ISM, although the velocity dispersion of the turbulence (2–4 km s −1) is lower than would be expected on these scales (7–10 km s−1). They estimate the Toomre Q parameters of their model discs and find that they equilibrate into marginally stable states. The star formation rate surface densities also settle into equilbria which are mostly well described by power laws resembling the SK law (although they also find this for their purely hydrostatic test case, so caution against over–interpretation of this result).
Ostriker and Shetty, (2011) and Kim et al., (2011) discuss a model of galactic evolution in terms of dynamical equilibria, where heating balances cooling, pressure balances gravity and turbulent driving balances dissipation. They inject momentum from star–forming events and take SNe to be the main sources of feedback. Radiative heating, which is assumed to come from massive stars proportionally to the star formation rate surface density, and from a constant galactic radiation field, is introduced via a volumetric heating rate. An equilibrium between the vertical gravitational acceleration and feedback–driven turbulence is rapidly achieved, heating and cooling and star formation rates settle into equilibrium, and thermal and turbulent pressures settle into nearly linear relations with the star formation rate surface density. This result, combined with the vertical dynamical equilibrium straightforwardly implies that the star formation rate surface density is proportional to the weight of the ISM.
Similar results are obtained in models of ULIRGs by Shetty and Ostriker, (2012), who include momentum input from supernovae. A dynamical equilibrium establishes itself on a timescale short compared to the orbital time within the disc in which the input momentum flux balances the vertical gravitational field. The SNe occur only in the densest gas in the midplane but are able to accelerate gas to altitudes of more than 100pc, driving turbulence and resulting in an ISM structure dominated by large shells.
Kim et al., (2013b) extend the work of Shetty and Ostriker, (2012) and Kim et al., (2011) to three–dimensional shearing–box calculations. They observe the formation of cold cloudlets by thermal instability which gravitate toward and merge with one another in the disc midplane. The models again globally reach a dynamical equilibrium, which includes formation and destruction of gravitationally bound clouds.
Numerous authors have come to the conclusion that the locations and times at which feedback is inserted into simulations are at least as important, if not more so, as the detailed physics implemented. Slyz et al., (2005) simulate a three–dimensional periodic non–driven turbulent box 1.28 kpc on a side. Star formation is taken to occur in collapsing and rapidly–cooling regions whose density exceeds a threshold. Matter and energy released by winds and SNe are injected, smeared out over a characteristic timescale of either the local dynamical time, or 10 Myr (whichever is smaller). The manner in which the supernovae are detonated strongly affects the resulting star formation rates. With the employed time delays, hot gas fills a progressively larger and larger fraction of the simulation box, driving up the density and star formation rate in the cool gas. However, if supernovae are detonated immediately in star forming gas, this does not occur and the star formation rates were observed to be up to two orders of magnitude lower. More recently, several other groups have explored the issue of the importance of supernova detonation sites. Gatto et al., (2015) obtain radically different results from detonating SNe randomly in their turbulent ISM, or at peaks in the cold gas density (arguably more likely explosion sites). Random driving produces an ISM almost entirely filled with very hot (106 – 107 K) gas with cold material being confined to clumps with small filling factors. Peak driving instead produces almost no very hot gas, although there are substantial volumes filled with gas at 104 K. The cold material has a much larger filling factor and a filamentary topology. Walch et al., (2014) use the supernova prescription of Gatto et al., (2015) and examine two additional means of specifying SN sites, namely a mixture of random and peak driving, and clustered random driving where the SNe are correlated with other but not with the dense gas. They find that clustering the SNe has only a minor effect. Peak and mixed driving both leave the galactic discs strongly concentrated at their mid planes, again with a filamentary distribution of cold gas. Random driving results in an outflow perpendicular to the disc.
Hennebelle and Iffrig, (2014) examine the influence of the supernova detonation scheme on star formation in their ramses models. Peak–driving reduces the star formation rates by factors of 20–30 owing to the rapid destruction of dense star–forming material. However, they also find that the details of the implementation of the supernova explosions themselves have a strong influence. Introducing the supernova energy in purely thermal form results in a star formation rate twice as high as injecting just five percent in kinetic form.
5.6.2. Whole–galaxy models of spirals
Although they allow one to achieve better resolution with given computational resources, vertical–slice or shearing box simulations require substantial physical components of spiral galaxies, such as spiral arms, to be parameterised. Truly satisfying simulations should of course reproduce these features self–consistently. Besides this, self–regulation of star formation in the disc plane is a different (though obviously related) question to the vertical equilibria between gravity and pressure discussed in the previous subsection.
In fact, the formation of realistic spiral galaxies, either individually or in the context of cosmological simulations is a long–running problem in computational astrophysics. The issue is catastrophic angular momentum loss, in which overcooling of collapsing baryons leads to the formation of too many low–angular–momentum spheroidal galaxies, and too few spirals. Early attempts to solve this problem include Katz and Gunn, (1991), Katz, (1992) and Navarro and White, (1994), which still produced discs that were too small and centrally concentrated. Abadi et al., (2003) suggested that the resolution of this issue lay in the regulation of star formation by feedback. The most important form of feedback at galactic scales has traditionally been considered to be supernovae.
Notwithstanding these issues, several authors reached the conclusion that many properties of spiral galaxies could be reproduced without the need to invoke feedback and that various instabilities, rotational shear and gravitational torques were of comparable or greater importance. Wada and Norman, (2001) find that gravitational and thermal instabilities produce a two–phase turbulent ISM in the absence of feedback. After implementing stellar wind and SN feedback from Lagrangian star particles, they observe that the overall morphology of their galactic discs and the gas density PDF are little changed. Both models produce velocity power–spectra indicative of turbulence, although the model without feedback has a steeper slope of -3, compared to -2 in the feedback model, which they attribute to the increased importance of shocks in the feedback calculation. Turbulence in both simulations is also driven by shear and self–gravity. Kravtsov, (2003) found that their simulations produce a good approximation to the SK law with or without feedback. In common with Wada and Norman, (2001), they find that the effect on the density PDF on galactic scales is small, although more low–density gas is produced by feedback. Similar results were reported by Wada and Norman, (2007), despite their rather high supernova rate of 1.5 × 10−3 yr−1 kpc−2. Renaud et al., (2013), who include SN and photoionising feedback in their ramses models of a Milky Way–type galaxy, concluded that feedback was not very efficient in destroying the clouds because of drift between the clouds and the star particles, ensuring that most supernovae do not explode inside clouds. Star formation was regulated more by large–scale turbulent support than directly by feedback.
Other groups have concluded that supernova feedback acting alone can be important, but only if either the supernova rate is increased to larger values than observed, as in the aforementioned studies, of if the individual supernova energies are increased. Shetty and Ostriker, (2008) perform two–dimensional simulations, some with an external potential to induce the formation of spiral arms, including the effects of SNe modelled as injection of momentum to avoid the overcooling problem. Star formation is restricted to gas above a density threshold and SNe are introduced probabilistically each timestep. Models with and without spiral potentials both required very strong levels of feedback to influence the evolution of these structures, resulting in positive feedback from the collisions of adjacent bubbles and a rough equilibrium between cloud formation and destruction. The overall effect is to decrease star formation rates, even if positive feedback occurs locally. In AMR simulations of disc galaxy formation, Agertz et al., (2011) included Type Ia and II supernova feedback, treating the star formation threshold density, efficiency and the supernova energy as free parameters. They found that the disc surface density profiles and relative contributions of gas and stars to the surface density depended strongly on the parameterisation of the star formation rate, whereas the self–regulation of star formation was controlled by the supernovae energies. They were only able to achieve self–regulation for explosion energies of 5 × 1051 ergs, rather higher than canonical values.
Many simulations are, however, significantly influenced by supernova feedback, both in terms of the rates of star formation and the structure of the resulting galaxies. These two issues are increasingly found to be connected – the distribution of star formation in time controls the final structure of simulated galaxies. Robertson et al., (2004) employ the Springel and Hernquist, (2003) multiphase ISM model to model a set of galaxy haloes. One of the ten most massive haloes in their simulation hosts a well–resolved disc galaxy with no strong bulge component, exhibiting instead an exponential surface brightness profile. Similar results are reported by Okamoto et al., (2005) and Scannapieco et al., (2008) who see that feedback suppresses early collapse, leaving large quantities of hot gas to cool at late times, from which an extended disc of young stars eventually form. More powerful feedback favoured the disc over the spheroid as expected, although the disc–to–spheroid mass ratio never much exceeded unity. Scannapieco et al., (2012) present the Aquila cosmological code comparison project, in which different implementations of feedback are tested against each other in different Eulerian and Lagrangian codes, as well as the arepo hybrid code. All the codes implement SN feedback, but using different schemes, although most inject SN energy in thermal form. Galaxy morphology is largely independent of which hydro scheme is employed and depends instead on the distribution of star formation in time. Forming realistic discs requires that feedback delay star formation so that it continues to late times. However, all the codes formed stellar discs which are too concentrated, implying a failure to prevent the accretion of low–angular–momentum material. This in turn is attributed to the inability of the feedback mechanisms employed to prevent a strong initial burst of star formation. Aumer et al., (2013) use gadget–3 simulations to study the formation of spiral galaxies in cosmological simulations. Supernova feedback is implemented along with radiation pressure, as in Hopkins et al., (2011). Feedback, in particular pre–supernova feedback, helps in production more realistic galaxies by delaying feedback to later times.
Galactic winds have a role to play in the angular momentum problem, since they preferentially expel low–angular momentum material from haloes. Additionally, real galactic discs have much smaller baryon quantities than simulations without feedback predict. IGM enrichment indicates that much of the IGM must have been inside halos at some point to be enriched, then expelled again. Galactic super winds with mass loss rates much larger than the SFR are generally required.
Tasker and Bryan, (2006) perform three–dimensional simulations using the enzo code, with similar star formation criteria and a similar technique to smear out the effects of Type II SNe feedback in time as Slyz et al., (2005). The major effect of feedback is to drive a kpc–scale galactic fountain, cycling gas out of the galactic plane, and causing the disc in general to puff up. Feedback also increases the star formation timescales so that it is at least to some extent self–regulating, but the star formation rates are still substantially higher than observed in real galaxies. Dubois and Teyssier, (2008) simulate the formation of stellar feedback–driven galactic winds in ramses. They allow star formation to proceed in the centre of an isolated rotating halo, forming a disc structure. Haloes with different masses, spin parameters, virial velocities and star formation timescales are considered, under the influence of SN feedback. In the low–mass (1010 M⊙) haloes, the combined SNe blow bipolar wind cavities, with compact discs forming in haloes with low spin parameters being the most efficient wind drivers. In the high–mass 1011 M⊙ haloes, the feedback–driven outflow is stalled by continuing accretion, leading to an accretion shock around the disc, and no galactic winds. They conclude that the infalling gas from the halo is a critical determinant in the formation of the wind. However, even in the low–mass haloes, the mass ejection efficiency is about an order of magnitude lower than observations suggest it should be, and they are unable to solve the overcooling problem in their simulations. Brook et al., (2012) use the gasoline SPH code to study the formation of galaxies over a wide range of masses. Early radiative feedback and supernovae are both implemented. Feedback–driven outflows remove low–angular momentum material, resulting in more realistic extended discs and removing dark matter cusps.
Supernovae are generally regarded as the most important feedback mechanism at galactic scales, but several authors have concluded that they cannot on their own reproduce observed galactic properties and that in fact other forms of feedback, such as HII regions and radiation pressure do have important contributions to make. Crain et al., (2015) make the point that the energy, momentum and mass fluxes into the ISM from star–forming regions and supernovae are not known, and nor are the magnitudes of the prompt losses of energy by radiation, and of momentum by cancellation. In any case, these losses occur at scales too small to be resolved.
Many groups have tackled this problem by varying the ‘strength' of feedback in their simulations and exploring the consequences for observable properties such as molecular cloud properties or the star formation rate. Dobbs et al., (2011), for example, simulate whole galactic discs in SPH with a background potential to model spiral arms. They include energy from supernovae split 2:1 between kinetic and thermal components, and with various assumed star formation efficiencies in dense gas. The higher star formation efficiencies (and therefore levels of feedback) produce populations of GMCs which are predominantly unbound and irregularly shaped, although they note that collisions between clouds also contribute substantially to their internal velocity dispersions. Dobbs and Pringle, (2013) quantify this result further and find that it is mostly the smaller (∼ 104 M⊙) clouds that are strongly affected by feedback, whereas the larger ∼ 106 M⊙ are more affected by shear. Dobbs, (2015) resimulate portions of Dobbs and Pringle, (2013)'s calculations at higher resolution and explore different prescriptions for the timing of the injection of supernova feedback, including delayed and stochastic models and smooth and instantaneous energy injection, but they find that in practice their choices have little impact on the outcome of their simulations.
Übler et al., (2014) explicitly test the effect of varying the strength of combined–feedback models. Their strong feedback model is derived from Aumer et al., (2013) and includes SNe kinetic and thermal feedback in a multiphase decoupled ISM as described by Springel and Hernquist, (2003), as well as radiation pressure, while their weak feedback model includes only SNe. The star formation efficiency of the weak–feedback model is always too high, and the resulting galaxy is spheroidal, whereas the strong feedback scheme gives disc–like stellar distributions and credible baryon conversion efficiencies at z=2–3, but too few stars at z=1. Higher star formation rates in the weak feedback case also result in older, redder stellar populations.
Ceverino et al., (2014) improve on the basic thermal feedback from winds and SNe in the art code (Kravtsov et al., 1997) by implementing radiation pressure feedback. They find substantial differences, with radiation pressure driving additional turbulence in galactic discs and destroying the most compact and high–column density clumps, which are similar to normal GMCs and substantially less massive than the giant clumps of the kind observed in moderate redshift galaxies (e.g. Genzel et al., 2011). The stellar distribution is correspondingly more extended and less concentrated, and star formation rates drop by factors of a few. The formation of smaller satellite galaxies is almost entirely terminated.
The potential of feedback to reduce the over–formation of stars in cosmological SPH simulations is explored by Stinson et al., (2013), who found that supernova feedback on its own is not sufficient and turn to pre–supernova radiative feedback. They do not include kinetic feedback as, for example, in Hopkins et al., (2011), because molecular clouds in their simulations are not resolved, being represented by only a few particles. They instead introduce thermal feedback over a 4 Myr period into these few particles. They do not disable cooling, so the gas rapidly cools to 104 K. The large–scale dynamical effects are negligible, but star formation is locally suppressed. They adjust the efficiency of energy uptake to reproduce the required stellar– to halo–mass ratio, and find that the resulting star formation rate is highly sensitive to this parameter.
A suite of AMR simulations of an isolated disc galaxy is executed by Agertz et al., (2013) in which the feedback prescription is varied. Momentum is injected either by momentum kicks or as a non–thermal form of pressure and different values of the IR optical depth for momentum absorption are tested, cooling delays of 10 or 40 Myr after energy injection are implemented, and a passively–advected decaying energy variable akin to that used by Teyssier et al., (2013) is also explored. They conclude that pre–supernova feedback is a crucial ingredient in their models, capable of reducing star formation rates and efficiencies by an order of magnitude on its own, and averting the overcooling problem by destroying dense gas before SNe can detonate inside it. This very rich suite of feedback models was used by Agertz and Kravtsov, (2015) to show that feedback is only effective in regulating star formation rates if local star formation efficiencies are high enough that there are strong spatial and temporal correlations between the injection of momentum and energy, but that in such cases, the results are sensitive to the details of the feedback prescription.
Moody et al., (2014) test two models of feedback in their simulations of the formation of galaxies, and in particular of the very massive (107 – 109 M⊙) and extended (∼ 1 kpc) clouds observed in star–forming galaxies at redshifts z ∼ 1−3 (e.g. Genzel et al., 2011). The first model encompasses only thermal feedback from stellar winds and SNe, modelled as a constant heating rate for 40Myr after a star formation event. The second model includes radiation pressure from the ionising radiation fields of the sources, suppressing the formation of lower–mass clumps, and slowing star formation by factors of around two. The addition of radiation feedback produces a much stronger decrease in the star formation rate in their simulations than SN feedback on its own, but they still find that they overproduce stars by factors of a few. They also find that stellar feedback reduces the bulge:disc ratio and produces discs with flat rotation curves, but which are too thick and only poorly rotationally–supported.
Schaye et al., (2015) implement star formation stochastically via a scheme proposed in Schaye and Dalla Vecchia, (2008) in which the rate is set by the local pressure, and which automatically reproduces the SK relation. Star formation events inject energy and momentum from radiation, winds and SNe. Energy is injected via a temperature increment to avoid spurious overcooling, with an efficiency factor which sets how much energy is available for feedback. They adjust parameters such as the density threshold for star formation and the efficiency of energy uptake, calibrating the results using the z = 0.1 galactic stellar mass function as a yardstick. Since feedback regulates the supply of gas to the ISM, the strength of feedback influences a wide variety of properties of the formed galaxy population, including central black hole masses, spatial concentration of stars, star formation rates and metallicity.
Other authors, in particular Hopkins et al., (2011), Hopkins et al., (2012), Hopkins et al., (2013) and Hopkins et al., (2014) attempt to model feedback in a physically–motivated manner with as few adjustable parameters as possible. These papers model isolated and merging galaxies of several different types – high–redshift objects, and local Milky Way–type and dwarf galaxies. The structures of the merging galaxies are largely controlled by gravitational torques, and the violently unstable high–redshift galaxy is less affected by feedback and more by gravitational instability. However, the ISM in their model galaxies generally reaches a steady state after a few dynamical times in which the star formation rate and feedback keep the galactic discs on the edge of Toomre instability, as observed by Koyama and Ostriker, (2009). Good approximations to the SK law emerge naturally from this state. For the larger galaxies, radiation pressure is the dominant feedback mechanism, particularly in driving large–scale outflows. However, the density of their dwarf model is low enough, and the corresponding cooling time long enough, that thermal feedback from SNe and winds become important. Hopkins et al., (2014) conclude that feedback is both necessary and sufficient to regulate star formation, but only when all their feedback mechanisms act in concert. The results of these simulations are an interesting contrast to those of Ostriker and Shetty, (2011) and Kim et al., (2011), who discuss vertical stability maintained by an equilibrium between gravity and dynamical pressure acting perpendicular to the disc plane.
Roskar et al., (2014) study disc galaxy formation in ramses and examine the importance of pre–supernova radiative feedback as well as supernovae. They vary the dust opacity so that the gas absorbs larger and larger quantities of momentum form the stellar radiation field. They find that radiation feedback is able to avert the overproduction of stars by expelling gas from their model halo. However, they also find that this result cannot be achieved without severely disrupting the morphology and dynamics of the disc.
Spiral galaxies have received a lot of attention from modellers, not least because we live inside one. However, dwarf galaxies are the building blocks of larger systems, are the most dark–matter dominated objects known, and are enigmatic in the sense that cosmological simulations produce many more of them than are actually observed. They are thus a rich field of study, and their smaller masses makes the effect of feedback upon them more dramatic.
Many authors have addressed the self–regulation of star formation in dwarf galaxies which can, under the influence of feedback, operate in the the so–called breathing mode (Stinson et al., 2007), where gas is expelled into the halo but eventually reaccretes to form a new generation of stars, which restart the cycle. This is described in detail by Kawata et al., (2014), who perform SPH simulations including stellar winds and SNe, with radiative cooling disabled for the duration of feedback. Star formation in the feedback simulation becomes intermittent, and large fractions of the galaxy volume are cleared of gas. The expanding bubbles driven by the earliest–forming stars collide with gas still accreting onto the galaxy and a second round of star formation is induced. Feedback from the second generation of stars increases the bubble size further, temporarily terminating star formation. However, the bubbles are not able to expel gas entirely from the galaxy's halo and it eventually reaccretes for yet another round of star formation.
Kim et al., (2013a) model dwarfs using the enzo code, injecting matter and energy from SNe with a characteristic time delay of 6Myr, and including transport of ionising radiation using the methods of Wise and Abel, (2011) and Kim et al., (2011), with star particles given ionising fluxes proportional to their masses during the 6Myr interval before the SNe. Both heating and momentum from the radiation field are included. They observe that star formation becomes self–regulating after a transient period of order 10 Myr, and that the addition of radiative feedback slows the star formation rate by roughly one fifth compared to models involving only SNe.
Some dwarf galaxy simulations reveal interesting parallels with simulations conducted at much smaller molecular cloud scales. Pawlik et al., (2013) use the traphic code to investigate the formation of the first galaxies under the influence of radiative feedback from the first stars. The primary coolant in the metal–free gas is rovibrationally excited molecular hydrogen, which is destroyed by Lyman–Werner band photons, so that stars deprive forming galaxies of their ability to cool. Secondly, hydrogen–ionising photons heat the gas, driving it out of haloes with virial temperatures lower than 104 K, and slowing accretion onto lower–mass objects. However, photoionisation also produces free electrons, catalysing molecular hydrogen formation and increasing the ability of the gas to cool. They find, as in smaller–scale simulations, that the effects of radiation are constrained by inhomogenous gas structures, in this case filamentary accretion flows feeding baryons into their simulated forming dwarf galaxy. The similarity between this and the process observed by Dale et al., (2005) is striking. The reduction in accretion is sufficient to terminate star formation, eventually enabling the gas to cool and to undergo another burst of star formation, by which time the halo is too massive to lose any further baryons due to feedback, and the second starburst lasts longer. The virial temperature of the halo becomes high enough to enable atomic hydrogen cooling and the galaxy forms stars continuously, although more slowly than in the case with no radiative feedback, anf it is the photoionisation heating and not the Lyman–Werner photodissociation that makes the difference. As the simulation proceeds, the gas baryon density in the halo rises and the expansion of the HII region is retarded by the high recombination rates (as in Dale et al., 2005 and Peters et al., 2010), at which point the simulation effectively ceases to respond to feedback. Radiative feedback also effects, via gas expulsion and redistribution, the dark matter distribution, decreasing the central density. The structure of the baryonic discs is largely unchanged, although photoheating suppresses star formation in neighbouring haloes as well.
Other authors model situations in which star formation is overall slowed or outright terminated by feedback. Wise et al., (2012), who consider radiation pressure from population III and II star formation, implemented using the scheme of Wise and Abel, (2011). They focus on the evolution of the most massive halo in their simulation, finding that radiation pressure reduces the overcooling problem and reduces star formation by a factor of ≈ 5. Thermal and momentum transfer from the stellar radiation field create a ∼ 100 pc expanding turbulent region centred on the main concentration of stars.
In many of these models, external feedback is at least as important if not more so than internal processes. Whalen et al., (2008) examine the external irradiation of minihaloes by massive primordial stars. Their results show interesting parallels with the much smaller–scale, present–day calculations of, for example, Bisbas et al., (2011). They show that radiative feedback accelerates star formation in relative dense and evolved haloes, but terminates it in more diffuse structures.
Petkova and Springel, (2011) used their optically–thin variable Eddington tensor radiation transport scheme to examine the feasibility of cosmic reionisation by star–forming galaxies, and the consequences on the global star formation rate. Photo–heating of the intergalactic medium significantly slows the accumulation of baryons in dark matter haloes, particularly for the lower–mass haloes, and slows star formation by a factor approaching two. Although they are mainly interested in the effects of supernovae, Sawala et al., (2010) find that background UV radiation is of crucial importance in their simulations. The combined mechanisms are sufficient to empty dwarf haloes of gas and terminate star formation by z = 6. Simpson et al., (2013) reached similar conclusions using enzo. Their halo's quantity of dense star–forming material is largely regulated by SN feedback, but the total gas fraction is largely set by photoheating, and once it is cleared of gas, it cannot reaccrete.
Reionisation and photoheating is also examined by Pawlik et al., (2015), who point out that reionisation is self–regulating. Photoheating boils gas out of low–mass haloes and shuts down accretion, lowering the ionising emissivities of galaxies. However, a positive feedback is also exerted, since the heating smooths out density inhomogenieties and reduces the recombination rate in the IGM. SN feedback also affects reionisation, since it clears out gas from low–mass haloes, shutting down star formation, although it also potentially locally triggers star formation and opens low–density escape routes for photons, which may enhance reionisation. Star formation is suppressed by almost an order of magnitude by feedback between z = 14 and z = 6, with SNe being much more significant than photoheating, although the two mechanisms complement each other, suppressing star formation more when acting together than alone. SNe suppress star formation evenly across most of the range of galactic masses, whereas photoheating suppresses star formation only in the lower mass haloes. In both cases, suppression occurs by destruction of dense gas and by reducing accretion.
The internal structures of dwarf galaxies are also sensitive to feedback. The core–cusp problem in dwarf galaxies is discussed by Teyssier et al., (2013). While pure N–body models predict that dark–matter haloes have central cusps, observations suggest that they instead have constant density cores. Of many possible solutions, the least outlandish is the modification of the baryon distribution and hence the dark–matter distribution by feedback. They examine this question with the ramses AMR code. The effect of feedback is to produce a thick, turbulent gas disc supporting outflows and emptying the central regions of baryons. The star formation rate is lowered, on average, by an order of magnitude and is much more staccato in nature. Gas cools and collapse, starting a burst of star formation which expels gas from the disc, shutting star formation down. However, gas falls back onto the disc and triggers another round of star formation, and the cycle repeats. The effect of gas removal form the central regions is indeed to transform the dark–matter distribution there from a cusp to a core after ≈ 0.5 Gyr.