The cosmic production of light nuclides is the result of weak and nuclear reactions in the context of an expanding, cooling universe. “Standard” BBN refers to the scenario for light element production which marries the Standard Model of particle physics with the “standard” (ΛCDM) cosmology, with:
Under these assumptions, the expansion of the universe is governed by the Freidmann equation
 |
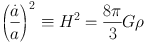(1) |
where a(t) is the
dimensionless cosmic scale factor (related to redshift z via
1 + z = 1 / a), and H =
/ a is the
universal expansion rate. The total cosmic mass-energy density ρ =
∑ρi sums
contributions from all cosmic species i.
By far the largest contribution to the density comes from radiation: relativistic species for which m ≪ T (with T the temperature), namely blackbody photons and Nν = 3 species of neutrinos and antineutrinos, and e± pairs at T ≳ me. Cosmic matter consists of nonrelativistic species with m ≫ T: nucleons n and p, and e− at T ≲ me. Since ρrad ≫ ρmatter, eq. (1) shows that radiation dominates cosmic dynamics during BBN.
BBN occurs entirely in this radiation-dominated epoch, for which the energy density has ρ ∝ T4, where T ∝ 1/a (adiabatic cooling). This, together with eq. (1), gives t ∝ 1 / T2, or
 |
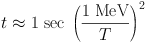(2) |
Light-element formation depends crucially on the relative amounts of baryons (nucleons) and radiation, parameterized by the baryon-to-photon ratio
 |
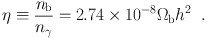(3) |
Here Ωb = ρb / ρcrit and ρcrit = 3H02 / 8π G, with H0 the present expansion rate (Hubble parameter). In standard BBN, η is the only free parameter controlling primordial light element abundances.
Initially, cosmic baryons are in the form of free nucleons n and p. For T ≳ 1 MeV and thus t ≲ 1 sec, weak interactions are rapid (rates per nucleon Γn ↔ p ≫ H) and thus
 |
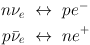(4) (5) |
drive neutron and protons to an equilibrium ratio
 |
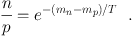(6) |
Thinking of the nucleon as a two-level system, this simply the Boltzmann ratio of the excited to ground state populations.
At T = Tf ≈ 1 MeV, the n−p interconversion (eq. 4) stop as the weak interaction “freezes out” (Γn ↔ p ≪ H), fixing n / p ≈ e−(mn−mp) / Tf ∼ 1/6. Deuterium production p(n, γ)d occurs, but is stymied by the large number of photons per baryon nγ / nb = 1 / η ∼ 109, which leads to effective deuteron photodissociation by the Eγ > Bd = 2.22 MeV tail of the Planck distribution. During this time, free neutron decay reduces the neutron-to-proton ratio to n / p ≈ 1/7.
At T ≈ 0.07 MeV, blackbody photons become ineffective to photodissociate deuterium. The deuteron abundance rapidly rises, and from this all of the light elements are built via strong (i.e., nuclear) interactions. A simplified reaction network appears in Fig. 1, highlighting the reactions which dominate production of the light nuclides. In contrast to much of stellar nucleosynthesis, for BBN the number of key reactions is small and well-defined, and all of the important reactions have been measured in the laboratory at the relevant energies; no low-energy extrapolations are needed.
 |
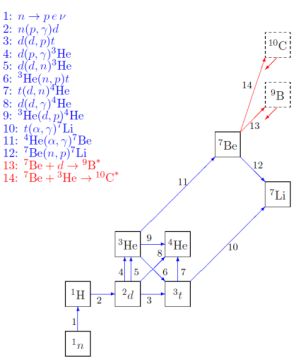Figure 1. Simplified BBN nuclear network: 12 normally important reactions shown in blue, and proposed/tested new reactions in red. |
Figure 2 shows the standard BBN light-element abundances as a function of the single free parameter η10 = 1010 η (eq. 3). The vertical yellow band is the WMAP η range (see Section 2.3). We see that the 4He abundance is weakly sensitive to η (note that the zero is suppressed in the top-panel abscissa). In contrast, deuterium drops strongly with η and 3He decreases substantially. The 7Li abundance is plotted after 7Be decay and thus sums both mass-7 species. 7Li production dominates the mass-7 abundance in the low η regime of the plot, while 7Be production dominates at the high-η regime, leading to the ‘dip” behavior.
 |
Figure 2. BBN theory predictions for light nuclide abundances vs baryon-to-photon ratio η. Curve widths: 1σ theoretical uncertainties. Vertical band: WMAP determination of η. |
The envelopes around the curves in Fig. 2 correspond to the 1σ uncertainties in the abundance predictions. These uncertainties are propagated from the error budgets–statistical and systematic–of the twelve dominant reactions shown in Fig. 1 (18, 19, 20, 21, 22, 23, 24, 25, 26, 12). The uncertainties in 4He are tiny (< 1%), those in D and 3He are small (∼ 7%), while the 7Li uncertainties are the largest (∼ 12% in the high-η regime of interest).
Several aspects of lithium production are noteworthy.
Mass-7 is produced both as 7Li and as 7Be;
the 7Be
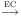7Li electron
capture occurs long after BBN ceases
(27).
The 3He(α,γ)7Be channel
dominates 7Be production.
Destruction occurs via 7Be(n, p)7Li
followed
by the rapid 7Li(p, α)4He reaction.
Finally, 6Li production in standard BBN is very small:
6Li/H ≃ 10−14, or
6Li/7Li ≲ 10−4
(28,
29).
2.2. Light Element Observations
Measuring the primordial abundance of any light element remains challenging. The BBN levels set at z ∼ 1010 are reliably accessible only in sites at z ≤ 3 and oftentimes z ∼ 0. Other nucleosynthesis processes have intervened, as evidenced by the nonzero metallicity of all measured astrophysical systems. Thus one seeks to measure light elements in the most metal-poor systems, and then to obtain primordial abundances requires extrapolation to zero metallicity . Our discussion will follow closely recent treatments in refs. (30, 31, 32).
2.2.1 DEUTERIUM, HELIUM-3, HELIUM-4 Deuterium can be measured directly at high redshift. It is present in distant neutral hydrogen gas clouds which are seen in absorption along sightlines to distant quasars. At present there are seven systems with robust deuterium measurements (33, 34, 35, 36, 37, 38). These lie around redshift z ∼ 3 and have metallicity ∼ 10−2 of solar; thus deuterium should be primordial. For these systems,
 |
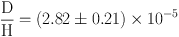(7) |
where the error has been inflated by a the reduced χν2 = 2.95.
Helium-4 can be measured in emission from nearby metal-poor galaxies (extragalactic H ii regions). The challenge is to reliably infer abundances at the needed ≲ 1% level. Several recent analyses differ due to systematics in the extraction of abundances from nebular lines (39, 40, 41, 42, 43). The mass fraction of (40)
 |
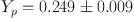(8) |
has the largest and most conservative measure of the error budget; the allowed range overlaps with analyses of other groups.
Helium-3 is at present only accessible in our Galaxy’s interstellar medium (44). This unfortunately means it cannot be measured at low metallicity, and so its primordial abundance cannot be determined reliably (45); we will not use 3He to constrain BBN.
2.2.2 LITHIUM-7 Lithium is measured in the atmospheres of metal-poor stars in the stellar halo (Population II) of our Galaxy. Due to convective motions, surface material in stars can be dragged to the hot interior where lithium is burned readily; this effect is seen in low lithium abundances in cool halo stars. Fortunately, the hottest (most massive) halo stars have thin convection zones, and show no correlation between lithium and temperature. We consider only lithium abundances in these stars.
Figure 3 shows lithium and iron abundances for a sample of halo stars (46). Li/H is nearly independent of Fe/H; this flat trend is known as the “Spite plateau” in honor of its discoverers (47). But heavy elements such as iron (“metals”) increase with time as Galactic nucleosynthesis proceeds and matter cycles in and out of stars. Thus the Spite plateau indicates that most halo star lithium is uncorrelated with Galactic nulceosynthesis and hence, lithium is primordial.
 |
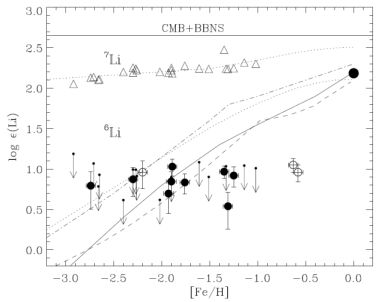Figure 3. Lithium abundances in selected metal-poor Galactic halo stars, from (46) with permission. Fore each star, elemental Li = 6Li + 7Li is plotted at the star’s metallicity [Fe / H] = log10[(Fe / H)obs / (Fe / H)⊙]. The flatness of Li vs Fe is the “Spite plateau” and indicates that the bulk of the lithium is unrelated to Galactic nucleosynthesis processes and thus is primordial. The horizontal band gives the BBN+WMAP prediction; the gap between this and the plateau illustrates the 7Li problem. Points below the plateau show 6Li abundances; the apparent plateau constitutes the 6Li problem. |
Moreover, the Spite plateau level measures the primordial abundance. Thanks to a sustained effort of several groups (46, 48, 49, 50, 51, 52, 53, 54, 55, 56), a large sample of halo stars have measured lithium abundances. The dominant error are systematic. A careful attempt to account for the full lithium error budget found (57)
 |
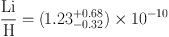(9) |
with this 95%CL error budget dominated by systematics (see also Section 3.1).
Finally, it is encouraging to note that lithium has now been seen in stars in an accreted metal-poor dwarf galaxy. The Li/H abundances are consistent with Spite plateau, pointing to its universality (58).
2.2.3 LITHIUM-6 Due to the isotope shift in atomic lines, 6Li and 7Li are in principle distinguishable in spectra. In practice, the isotopic splitting is several times smaller than the thermal broadening of stellar lithium lines. Nevertheless, the isotopic abundance remains encoded in the detailed shape of the lithium absorption profile.
High-spectral-resolution lithium measurements in halo stars attain the precision needed to see isotope signatures. 6Li detections have been claimed, in the range (46)
 |
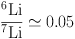(10) |
Fig. 3 shows the inferred 6Li/H abundance for some of these stars; its constancy with metallicity is strikingly reminiscent of the ordinary Spite plateau and similarly seems to suggest a primordial origin.
Lithium-6 observations remain controversial. It has been argued that stellar convective motions can alter the delicate lineshapes and mimic 6Li (59). Thus there are only a few halos stars for which there is widespread agreement that 6Li has even been detected. Thus, the conservative approach is to take the 6Li observations as upper limits, though it is of interest to see what is required to explain the “6Li plateau,” if it exists. Regardlessly, the isotopic searches confirm that most of primordial lithium is indeed 7Li.
2.3. Microwave Background Anisotropies as a Cosmic Baryometer
It is difficult to overstate the cosmological impact of the stunningly precise CMB measurements by WMAP and other experiments. The temperature and polarization anisotropies encode a wealth of cosmological information. Temperature fluctuations robustly record acoustic oscillations of the (re)combining baryon-photon plasma within dark matter potential; for a review, see (60). One of the most precise and robust results is the measurement of the cosmic baryon density and thus of η.
Figure 4 shows the sensitivity of the temperature anisotropy to the baryon density, as a function of angular scale (multipole) on the sky. Broadly speaking, increasing baryon density amplifies the odd peaks and depresses the even peaks. Accurate measurements of these peaks by WMAP and other experiments pins down the baryon density. The most recent 7-year WMAP data release gives
 |
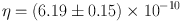(11) |
a 2.4% measurement!
 |
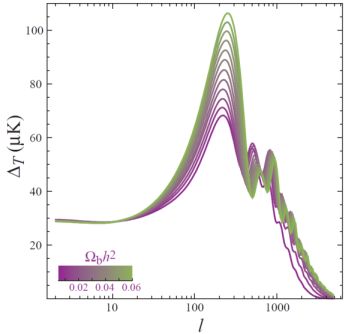Figure 4. CMB sensitivity to cosmic baryon content. Predictions for temperature anisotropy (rms of temperature fluctuation ΔT2 = ⟨ Tℓ ⟩2 − ⟨ T ⟩2) plotted as a function of angular scale (multipole ℓ, roughly corresponding to angular size 180∘/ℓ). Baryon density is seen to be encoded in the values and particularly the ratios of the peak heights. Figure from (60), with permission. |
2.4. Assessing Standard BBN: the Lithium Problem(s) Revealed
Prior to WMAP, BBN was the premier means of determining the cosmic baryon density. Standard BBN has one free parameter, η, but three light elements have well-measured primordial abundances: D, 4He, and 7Li. Thus the problem is overdetermined: each element ideally selects a given value of η, but allowing for uncertainties actually selects a range of η. If the different ranges are concordant, then BBN and cosmology are judged successful, and the cosmic baryon density is measured. This method typically specifies η to within about a factor ∼ 2 (61, 62).
The exquisite precision of the CMB-based cosmic baryon density suggests a new way of assessing BBN (9, 10). We exploit the CMB precision by using ηmwap as an input to BBN. This removes the only free parameter in the standard theory. Propagating errors, we compute likelihoods for all of the light elements. Fig. 5 shows these likelihoods (30) based on WMAP data (63). Also shown are measured primordial abundances as discussed above.
 |
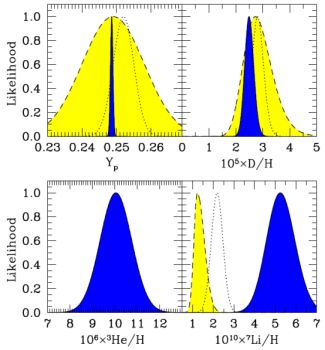Figure 5. Comparison of BBN+WMAP predictions and observations, from (30). Plotted are likelihood distributions for light nuclide abundances. Blue curves: theory likelihoods predicted for standard BBN using the cosmic baryon density determined by WMAP (63). Yellow curves: observational likelihoods based on primordial abundances as in Section 2.2. Dotted curves: observational likelihoods for different analyses of abundance data; the difference between these and the yellow curves gives a sense of the systematic errors. Note the spectacular agreement of D/H, and in contrast the strong mismatch between 7Li theory and data, which constitutes the lithium problem. |
Figure 5 shows that deuterium observations are in spectacular agreement with predictions–the likelihoods literally fall on top of each other. This concordance links z ∼ 3 abundance measurement with z ∼ 1010 theory and z ∼ 1000 CMB data, and represents a triumph of the hot big bang cosmology. We also see that 4He predictions are in good agreement with observations. And, as noted in Section 2.2, no reliable primordial 3He measurements exist.
Turning to 7Li, the BBN+WMAP predictions and the measured primordial abundance completely disagree: the predictions are substantially higher than the observations. Depending on the treatment of systematic errors in the measured Li/H, the discrepancy is a factor Libbn+wmap / Liobs = 2.4−4.3, representing a 4.2−5.3 σ discrepancy. This substantial mismatch constitutes the lithium problem (i.e., the 7Li problem).
Finally, as noted in Section 2, standard BBN predicts an unobservable 6Li/H abundance and 6Li / 7Li ratio far below the putative 6Li plateau. To the extent that the 6Li plateau is real, this would constitute a second Li problem–the 6Li problem.
Hereafter we will focus largely on the well-established 7Li problem, but where appropriate we will mention the 6Li problem.