


We have seen that the lithium problem was brought into sharp relief with the advent of the WMAP era, has become increasingly acute since. Possible solutions fall in three broad classes corresponding which part of the preceding analysis is called into question:
We consider each in turn.
We first consider the possibility that BBN predictions are sound, i.e., standard cosmology and particle physics are correct, and the nuclear physics of mass-7 production is properly calculated. If so, then the measured value of the primordial lithium abundance must be in error. In particular, the true value must be higher by a factor 3–4.
As described in Section 2.2, lithium abundances are measured via absorption lines in the photospheres of primitive, low-metallicity stars. For each star, the lithium line strength is used to infer the Li/H abundance. Lithium abundances are nearly insensitive to metallicity (Fig. 3)–this Spite plateau implies that lithium is independent of Galactic nucleosynthesis and is primordial, and the plateau level is taken as the primordial abundance. If missteps exist in this chain of reasoning, the lithium problem could potentially be alleviated.
For example, systematic errors could shift Li/H ratios in each star. We seek the total lithium content of the stellar photosphere, i.e., summed over all ionization states. However, the single (!) accessible 670.8 nm lithium line is sensitive only to neutral Li0. But in the stars of interest, lithium is mostly singly ionized. One must therefore introduce a large ionization correction Li+ / Li0 that is exponentially sensitive to the stellar temperature. Thus, a systematic shift upward in the temperature scale for halo stars would increase all stellar Li abundances and raise the Spite plateau towards the BBN+WMAP prediction.
In practice, accurate determination of stellar temperatures remains non-trivial, because the emergent radiation is not a perfect Planck curve (else no lithium lines!), nor is local thermodynamic equilibrium completely attained in the stellar atmospheres. Quantitatively, the needed systematic shift in the temperature scale is about ΔTeff ≃ 500−600 K upward, a ∼ 10% increase over fiducial values (outside of previous claimed errorbars) (64). A re-evaluation of one method to determine stellar temperatures indeed corrects the scale, typically by ∼ +200 K (65). However, later detailed studies of the stellar temperature scale are in good agreement with the fiducial temperature scale, leaving the lithium problem unresolved (54, 66).
An entirely separate question remains as to whether a star’s present lithium content reflects its initial abundance in the star. If the halo stars have destroyed some of their lithium, their present Li/H ratio sets a lower limit to the primordial lithium abundance. Indeed, given the low nuclear binding of 7Li, it need only be exposed to relatively low stellar temperatures (T ≳ 2.5 × 106 K) to suffer substantial destruction over the many-Gyr lifespan of a halo star.
Lithium depletion is a major diagnostic of stellar structure and evolution (67, 68, 69, 70). For stars of solar composition, lithium destruction (71, 72). (72) has long been studied in stellar evolution models. The major effect is convection, which circulates photospheric material deep into the interior (though still far from the stellar core) where nuclear burning can occur. Models for the evolution of low-metallicity stars, appropriate for the Spite plateau, now include numerous mixing effects which can change the photospheric lithium: convective motions, turbulence, rotational circulation, diffusion and gravitational settling, and internal gravity waves (70, 73, 74, 75). These effects must occur at some level, and models have some success in fitting some observed trends in halo stars. There is general agreement that for stars with low metallicities, convective zones are substantially shallower than in solar-metallicity stars, and so depletion such be much smaller than the factor ∼ 102 in the Sun (76). However, it remains difficult for models to quantitatively fit all of the data (49).
Thus observational efforts to find clues for lithium depletion in the Spite plateau stellar data themselves remain of utmost importance. One study found the Spite plateau in field halo stars to be very thin, with no detectable star-to-star variations around the Li-Fe trend, which showed a small positive slope in Li/H vs Fe/H (48). A small lithium increase with metallicity is required due to contamination from Galactic cosmic-ray production of 7Li and 6Li (57). An analysis of lithium and iron abundances in stars from the same globular cluster found trends consistent with lithium depletion via diffusion and turbulent mixing; some models suggest these effects could remove the lithium problem entirely (50). However, systematic differences between globular cluster and field star lithium abundances raise concern about globular clusters at sites for constraining primordial lithium (56).
Recently, several groups have found that at very low metallicity, [Fe / H] ≲ −3, lithium abundances on average fall below the Spite plateau (i.e., below the levels seen at metallicities −3 ≲ [Fe / H] ≲ −1.5) (52, 53, 51, 55). These groups also find that the star-to-star scatter in Li/H becomes significant below [Fe / H] ≲ −3. This appears to confirm the presence of significant lithium depletion in at least some halo stars.
The recent evidence for lithium depletion at very low metallicities is a major development, yet its implications for primordial lithium remain unclear. No significant scatter is detected in plateau stars with −3 ≲ [Fe / H] ≲ −1.5. Also, in no stars is Li/H seen above the plateau, and in no metal-poor stars is Li/H near the WMAP+BBN value. Finally, while 6Li measurements are difficult and controversial, there is general agreement that 6Li is present in at least some plateau stars. This much more fragile isotope strongly constrains thermonuclear burning processes–if stellar material is exposed to temperatures hot enough to significantly reduce 7Li, 6Li should be completely destroyed. (77).
To summarize, determination of the primordial lithium abundance continues to be the focus of rapid progress. At present, however, the observational status of primordial lithium remains unsettled. A purely astrophysical solution to the lithium problem remains possible. On the other hand, the observed lithium trends–particularly the small lithium scatter in temperature and metallicity, and the presence of 6Li–strongly constrain (but do not rule out) solutions of this kind. Consequently, it is entirely possible that the lithium problem cannot be resolved astrophysically, and thus we are driven to seek other explanations of the discrepancy; we now turn to these.
3.2. Nuclear Physics Solutions
We now consider the possibility that the measured primordial lithium abundance is correct, and the Standard Model of particle physics and the standard cosmology are also sound. In this case, the lithium problem must point to errors in the BBN light element predictions, in the form of incorrect implementation of standard cosmological and/or Standard Model physics.
However, the standard BBN calculation is very robust and thus difficult to perturb. As summarized in Section 2, standard BBN rests on very well-determined physics applied in a very simple system. The cosmological framework of BBN is that of a very homogeneous universe (guaranteed by the smallness of the observed CMB temperature fluctuations (3)), with a cosmic expansion governed by exact expressions in General Relativity. The microphysics is that of the Standard Model, also very well-determined. The relativistic species, which comprise cosmic radiation that dominates the energy density, are very well thermalized and thus their properties are that of Bose-Einstein and Fermi-Dirac gasses, for which exact expressions are also available.
The weak and strong (i.e., nuclear) interactions are also well-grounded in theory and calibrated empirically, but for BBN the needed physics is complicated (nuclear networks are large) and lies the farthest from first principles. Thus, these are the only possible “weak links” in the standard BBN calculation, and it is here that solutions to the lithium problem have been sought.
3.2.1. NEW AND REVISED REACTIONS One possibility is that weak and nuclear reactions in the BBN calculations are miscalculated due to reactions that are entirely missing, or that are included but whose rates are incorrect. But as described in Section 2 and seen in Fig. 1, only a relatively small number of reactions have been found to be important for producing the light elements, and all of these have been measured in the laboratory at the relevant energies. Their uncertainties have also been calculated and propagated through the BBN code, and are folded into the likelihoods appearing in Fig. 5. Moreover, BBN calculations use a much more extended reaction network than the simplified view of Fig. 1, with all initial state pairings of A ≤ 7 species present but most practice unimportant (78, 79, 23, 80, 81, 82, 83). Thus, to change the primordial lithium predictions requires surprises of some kind–either (i) the cross sections the known important reactions have uncertainties far beyond the quoted errors, or (ii) the cross sections for normally unimportant reactions have been vastly underestimated.
For the important reactions seen in Fig. 1, mass-7 production is dominated by the single reaction 3He(α, γ)7Be. While the quoted error budget in the measured cross section is small, ∼ 7% (84), absolute cross sections are difficult to measure. However, this reaction is also crucial in the production of solar neutrinos. To fix the cosmic lithium problem, the 3He(α, γ)7Be normalization would need to be low by a factor 3−4; if this were the case, the 7Be and 8B solar neutrino fluxes would be lower by a similar factor. Thus we can view the sun as a reactor which probes the 3He(α, γ)7Be rate, and the spectacular and precise agreement between solar neutrino predictions and observations becomes a measurement of the rate normalization which confirms the experimental results and removes this as a solution to the lithium problem (85).
Weak rates in BBN have received a great deal of attention over the years (86, 87, 88, 89, 90, 91, 92, 93, 94). The basic n ↔ p interchange rates (eq. 4) are most accurately normalized to the neutron lifetime. Corrections to the tree-level rates have ≲ 1% effects on abundances, and thus are far too small to impact the lithium problem (94).
Corrections to the standard thermonuclear rates have been considered as well. The effects of nonthermal daughter particles has been studied and found to be negligible (95, 82). Plasma effects, and electron Coulomb screening are also unimportant (96).
Turning then to (normally) subdominant reactions, Angulo et al. (97) noted that the (nonresonant) cross section for 7Be(d, α)αp was poorly determined and could solve the lithium problem if it were a factor ∼ 100 larger. They measured the cross section at BBN energies, but found values a factor ∼ 10 smaller than had been used.
Finally, the possibility of entirely new reactions has been recently studied by Boyd et al. (82). These authors systematically considered a large set of reactions, some of which have been neglected in prior calculations. The focus of this study is almost exclusively on nonresonant reactions, with the result that even when allowing for extremely large systematic uncertainties in known cross sections, most new channels remain unimportant. The loophole to this analysis is the presence of new or poorly measured resonances.
3.2.2. RESONANCES Both standard and nonstandard reaction pathways to primordial mass-7 are firmly anchored to experimental data. The only remaining new nuclear physics can only intervene via resonances which have evaded experimental detection or whose effects have been underestimated. Cyburt and Pospelov (98) point out that the production of the known resonance 7Be + d → 9B*(16.71 MeV) is poorly constrained experimentally; this reaction appears in Fig. 1. Within current uncertainties, this resonance could promote the 7Be+d channel to become the dominant 7Be destruction mode, and solving the lithium problem in an elegant manner.
Generalizing the Cyburt and Pospelov (98) suggestion, ref. (99) searched the entire resonance solution space for BBN. These authors systematically considered all compound states created in mass-7 destruction, via all possible 2-body reactions of the form (n, p, d, t, 3He,4He)+(7Li, 7Be). Most possibilities were found to be unimportant. However, in addition to the 7Be + d → 9B*(16.71 MeV) resonance, two other potentially important states were identified. The 7Be + t → 10B*(18.80 MeV) resonance is known and within present uncertainties could be significant. On the other hand, there is little data on high-lying states of 10C, but if a 10C*(15.0 MeV) exists and has J π = 1− or 2−, this also could bring cosmic lithium into concordance if the reaction widths are large enough. This last possibility would be a homage to Fred Hoyle’s celebrated prediction of the 12C*(7.65) state which solved the “carbon problem” of stellar nucleosynthesis (100).
Fortunately all of these states are experimentally accessible. To identify or exclude them marks the endgame for a nuclear solution to the lithium problem.
3.3. Solutions Beyond the Standard Model
Finally, we turn to the most radical class of solutions the lithium problem. Namely, we assume that primordial lithium has been correctly measured, and that the nuclear physics of BBN has been calculated correctly and holds no surprises. In this case, we are forced to question the assumptions underlying the standard BBN calculation, i.e,. we must go beyond the Standard Model of particle physics and/or the standard cosmology. For details beyond the overview below, see refs. (16, 15).
3.3.1. DARK MATTER DECAY AND SUPERSYMMETRY The existence of dark matter is now well-established, and its cosmic abundance has been inferred precisely; for recent reviews, see refs. (101, 102, 103). If dark matter takes the form of a relic particle created in the very early universe, it must be nonbaryonic. No Standard Model particles have the right properties, and thus dark matter demands physics beyond the Standard Model. Dark matter must of course be present during BBN, but ordinarily is assumed to be both nonrelativistic and weakly interacting, hence unimportant to cosmic dynamics and microphysical interactions. Similarly, dark energy is assumed to be negligible.
While the identity of the dark matter is unknown, a simple, popular, and physically well-motivated possibility is that dark matter today consists of relic weakly interacting massive particles (WIMPs). In particular, if the universe begins with equal abundances of WIMPs and anti-WIMPs (if the two are distinct), then their abundance today is determined by the freezeout of their annihilations. Famously, to reproduce Ωm ≃ 0.3 today, the annihilations must occur at ∼ TeV scales (well before BBN). By happy coincidence, this is also the scale of the weak interaction, and of current accelerator experiments–this is the “WIMP miracle” (101, 102, 103).
Moreover, it is likely that WIMPs today are the stable endpoints of a decay cascade. If so, then the WIMPs are the daughters born in the decays of the next-lightest particles in the cascade. The nature of these decays is model-dependent, but in general produce Standard Model particles which interact with the background plasma. If the decays occur during or after BBN, the interactions can change light element abundances (104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117), and thus potentially could solve the lithium problem(s) (118, 119, 120, 121, 122, 123, 124, 32).
We thus consider the effects of decaying massive particles during or after BBN. To get a feel for the basic physics, consider a particle X (and X if they are distinct) with mass mX ≫ mp, which decays with lifetime τX. The decays can have electromagnetic and/or hadronic channels, and given the massive nature of X, these decay products will be very relativistic and thus nonthermal.
As these electromagnetic and/or hadronic cascades thermalize in the cosmic environment, they interact with the light elements, largely via fragmentation (photodissociation or spallation). For example, high energy nucleons N fragment 4He:
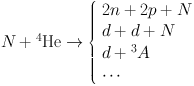 |
(12) |
This reduces the 4He abundance, but more importantly creates new deuterium and 3He. Furthermore, the secondary particles in eq. (12) are themselves nonthermal, and can initiate further interactions with the background thermal light nuclides. Of particular importance is the conversion of 7Be into 7Li with secondary neutrons
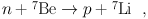 |
(13) |
which substantially enhances mass-7 destruction because of the lower Coulomb barrier for 7Li. Also of interest is the nonthermal production of 6Li via secondary nonthermal deuterons
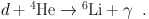 |
(14) |
Clearly, both of these processes are of great interest for both lithium problems.
Figure 6 shows light-element abundances in the presence of a hadronically decaying particle X. Abundance contours are plotted as a function of decay lifetime τX, and the pre-decay X abundance
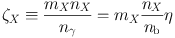 |
(15) |
In the absence of X decays, cosmic expansion dilutes baryons and X particles in the same way, and thus ζX remains constant. Figure 6 is for a hadronic branching fraction Bh = 1, i.e., all decays produce hadrons.
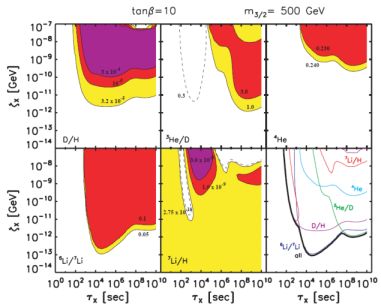 |
Figure 6. Effect of nonthermal particle injection on light element abundances, from (31). Each panel shows abundance contours in the presence of the hadronic decay of a (neutral) particle X, plotted as a function of X abundance ζX (eq. 15) and mean life τX. Results are shown for a hadronic branching ratio Bh = 1. As summarized in the last panel, the parameter regions where the 7Li problem is solved also lead to deuterium production, placing the two in tension. |
In each panel of Fig. 6, the colored areas indicate parameter regions where the predicted light element abundances disagree with observations, while the remaining white regions are allowed. At fixed τX, the light element perturbation is proportional to the X abundance. The limit ζX → 0 lies at the bottom of the plot, and corresponds to the unperturbed (standard BBN) case. At fixed abundance ζX, the light element effects strongly depend on particle lifetime, which determines when the light elements are perturbed. For example, at τX ≲ 10 sec, decays occur before the light elements are formed, and so the light elements are unaffected. Hadronic decays dominate the perturbations in the τX ≲ 106 sec of most interest here; electromagnetic decays dominate at longer times.
In the 7Li/H panel, the colored regions include the unperturbed low-ζX regime, reflecting the lithium problem for standard BBN. However, for a relatively narrow region with lifetimes τX ∼ 102 − 103 sec, that the 7Li abundance is reduced and brought into accord with observation. This arises due to the production of secondary neutrons (eq. 12), which facilitate mass-7 destruction via 7Be-to-7Li conversion (eq. 13); at longer lifetimes the secondary neutrons decay. For 102 − 103 sec lifetimes to be viable, however, the other light elements must remain in concordance. As seen in the final, summary panel, in the regime in which 7Li is reduced, all other constraints are satisfied except D/H, which is unacceptably high due to secondary deuteron production. This tension between deuterium and 7Li is a fundamental feature of decay scenarios, and as we see may allow for solutions but requires fine tuning.
Supersymmetry provides well-motivated candidates for decaying dark matter (125, 126, 127). Supersymmetry doubles the particle content of nature by requiring opposite-statistics (fermion ↔ boson) partners for every known particle. These partners are produced copiously in the very early universe. The lightest supersymmetric partner (LSP) is the stable end product of the decays of higher-mass supersymmetric particles, and naturally becomes a dark matter candidate (128, 129). These decays are a fundamental aspect of supersymmetric dark matter, and thus supersymmetric scenarios demand that particle decays occur. Moreover, even in the simplest scenarios–i.e., the constrained minimal supersymmetric Standard Model–the lifetime of the next-to-lightest supersymmetric partner can be long: ≳ 100 sec. Thus, minimal supersymmetry holds the tantalizing possibility of solving the lithium problem.
Figure 7 illustrates the interplay between supersymmetry and the lithium problem (32). The context is minimal supersymmetry in which the spin-3/2 gravitino is the next-to-lightest partner, which decays into the LSP neutralino that comprises the dark matter today. For a benchmark scenario in this model, the superpartner mass spectrum, lifetimes, and decay products are calculated. These are used to compute light element abundances, with nuclear uncertainties propagated; the results are compared to observations. The resulting χ2 is plotted as a function of gravitino mass m3/2 and pre-decay abundance ζ3/2. At low ζ3/2, we recover the unperturbed, standard case, where χ2 ≈ 32 for one effective degree of freedom (3 light elements − 2 parameters), a poor fit. At high ζ3/2, the light element perturbations are worsened over the standard case, and these supersymmetric parameters are excluded by BBN. Most interestingly, along the diagonal loop, the fit improves, and in the interior “islands,” χ2 drops below 6, corresponding to ∼ 2.4 σ. This region shows substantial improvement over standard BBN, and physically arises as the regime of optimal tradeoff between 7Li destruction and deuterium production. This region thus tantalizingly stands as a possible supersymmetric solution to the lithium problem, albeit statistically marginal and fine-tuned.
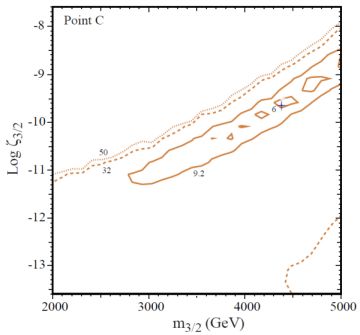 |
Figure 7. Light element constraints on gravitino decays in the context of the constrained minimal supersymmetric Standard Model, from (32). Shown are χ2 contours based on light element abundance constraints and 1 effective degrees of freedom, over the space of gravitino mass m3/2 and abundance ζ3/2 (eq. 15). The cross indicates the maximum χ2. diagonal “archipelago” shows the region where the lithium problem is greatly reduced by trading off 7Li destruction for some degree of deuterium production. |
Finally, in very recent years an entirely new aspect of decaying dark matter alteration of BBN has emerged. If the decaying particles are electrically charged, then the negatively charged dark matter can form bound states with charged nuclei, such as (pX−), (4HeX−), and (7BeX−). As pointed out by Pospelov (117), these bounds states unleash a rich array of new effects, in addition to the perturbations accompanying X− decays. For the heavy X− of interest, the binding energy of (AZX−) is B = Z2 A α2 mp/2 ≈ 30 Z2 A keV, comparable to nuclear binding. The Bohr radius is a = (2 α Z A mp)−1 ≈ 1 A−1 Z−1 fm, comparable to nuclear sizes. Bound-state Coulomb barriers are thus reduced and (7BeX−) becomes easier to destroy.
Beyond these basic effects, a new “bound state chemistry” can occur, whose nature is still under active study. One important effect (117) is catalysis, particularly d + (4HeX) → 6Li + X which enhances 6Li production far above the ordinarily small radiative capture d(α, γ)6Li. This can enhance 6Li production by orders of magnitude, possibly addressing the 6Li problem if real, but oftentimes overproducing 6Li. Rates for catalyzed reactions have recently been calculated to high precision (130). Intriguingly, (8BeX−) states have a binding energy very close to the energy for 8Be → α α breakup; if the binding energy is larger, then (8BeX−) is stable and can allow for cosmological production of 9Be (122, 131).
The general properties of X− recombination and bound states, and their impact on BBN, have been studied in refs. (117, 132, 123, 133, 122, 15). Looking at bound state effect only (i.e., ignoring decay effects), catalyzed 7Be destruction is effective and catalyzed 6Li is not overproduced, for sufficiently large X− abundance in the regime τX ∼ 2000 sec (132). Indeed, there exist regions of parameter space wherein both the 7Li and 7Li problems are solved. Full calculation of bound state and decay effects together is required to verify if solutions remain in specific detailed models; early calculations confirm solution space exists around τX ∼ 103 (134, 123).
Catalyzed production of 9Be also occurs and is constrained by the non-observation of a beryllium “Spite plateau;” the resulting limits on τX are comparable to those imposed by limits on primordial 6Li (122). 9Be constraints have the added advantage that they rely on elemental abundances which are much simpler to obtain reliably than isotopic abundances. However, very recently 9Be was investigated using updated catalysis rates from ref. (130), which greatly reduce the 9Be production rate. The resulting 9Be abundance then is quite small, below observable levels (131).
Bound-state effects are important in the context of minimal supersymmetry. Substantial parameter space exists in which the gravitino is the LSP and thus the dark matter, while the next-to-lightest partner is the charged stau τ±, the scalar partner to the tau lepton. These models are probed by bound-state BBN, which imposes constraints that are complementary to accelerator limits (121, 132, 135, 133, 134, 122, 124, 136). Indeed, the solutions to the 7Li and possibly also the 6Li problem which exist at τX ∼ 1000 sec could be interpreted as support for these models.
To summarize, decaying dark matter scenarios introduce a rich array of novel processes that can alter light elements during and after BBN. Moreover, such scenarios find well-motivated origin in supersymmetric cosmologies. Indeed, decaying-particle BBN offers important constraints on supersymmetry. Furthermore, the 7Li and possibly also 6Li problems can be solved in decaying particle scenarios which are realized in plausible minimal supersymmetric scenarios. This area is ripe for further theoretical, observational, and experimental development.
3.3.2. CHANGING FUNDAMENTAL CONSTANTS Observations of multiple atomic transitions in metals residing in high-redshift quasar absorption systems test fundamental physics in environments at great spacetime separations from our own; for a review see ref. (137). Surprisingly, some data hint at variations in the fine-structure constant at z ∼ 3, showing δ αEM / αEM ≃ −0.5 × 10−5 at the ∼ 5σ level, while others find results consistent with no variation. Thus the observational situation is unsettled, but intriguing.
Time variations in low-energy physics can be accommodated and are even expected in the context of some unified theories which in general predict stronger variations at earlier times. Moreover, an underlying unified theory implies that all Standard Model couplings and particle masses should vary, with definite but model-dependent interrelationships.
There is thus theoretical impetus, and some observational motivation, to contemplate changes in fundamental constants during BBN. The change in light elements depends on which parameters (couplings, masses) change, and on the size of the perturbations (138, 139, 140, 141, 142). In general, there is large model-dependence in quantifying the these variations, the links among them, and their manifestation in nuclear properties (masses, binding energies, cross sections).
An alternative approach is to turn the problem around and to consider the BBN implications of variation in nuclear physics parameters (143, 144). Coc et al. (140) systematically study the light-element response to variations in αEM, the electron mass me, the neutron lifetime τn, the neutron-proton mass difference mn − mp, and the deuteron binding energy Bd. Of these, the most sensitive parameter is the deuteron binding energy. A change of −0.075 ≲ δ Bd / Bd ≲ −0.04 lowers the 7Li abundance into concordance, without perturbing 4He or D/H beyond their observed error range. Thus, unified models which predict changes of this order can solve the lithium problem.
3.3.3. NONSTANDARD COSMOLOGIES The lithium problem could indicate nonstandard cosmology rather than particle physics. One recent such proposal is that cosmic acceleration could result from large-scale inhomogeneities in the cosmic density. Isotropy constraints can be satisfied if we occupy a privileged view from nearly the center of a spherically symmetric cosmic underdensity, which only returns to the cosmic mean at horizon-scale distances (145). Such a scenario explains cosmic acceleration within General Relativity, and without invoking dark energy, but must abandon the cosmological principle, instead requiring that ours is a privileged view of the universe.
Esthetics aside, observations probe such an inhomogeneous cosmos. BBN occurs differently in such a universe, if the baryon-to-photon ratio varies along the inhomogeneity. In particular, ref. (146) emphasizes that the observations of 7Li are made locally, at low z, while D/H and the CMB are both measured in the distant universe at high z. If the local baryon-to-photon ratio η0 is low by a factor ∼ 2, then indeed one would expect local 7Li to fall below the WMAP prediction, while D/H would agree.
This clever scenario however must face an array of observational tests. Relaxed galaxy clusters probe the cosmic baryon-to-matter fraction, and show variations ≲ 8% out to z ∼ 1, far less than the ∼ 50% variation needed for lithium abundances (147). Moreover, local measurements of D/H even more directly constrain the local η measurement. Because some stellar destruction may well have occurred, the local D/H sets a lower limit to the primordial abundance. In the lower halo of our own Galaxy, D / H = (2.31 ± 0.24) × 10−5. This value is in good agreement with the high-z D/H measurements and the WMAP+BBN predictions; it is therefore inconsistent with the low η needed for a low local 7Li / H.
Other nonstandard cosmology scenarios have been proposed to solve the lithium problem. One suggests that a large fraction (∼ 1/3 − 1/2) of baryons were processed through the first generation of stars (Population III) which ejected lithium-free matter (148). Such models face grate difficulties due to the substantial D/H depletion and 3He production which must also occur (149, 150).