In the remainder of this paper, we turn to questions about the very early universe: roughly speaking, about times earlier than t = 10−11 seconds, which as we saw in Section 3 represents the "boundary" of our confirmation of the standard model of particle physics. We will confine ourselves to the most widely accepted framework for understanding this regime: inflation. 13 Thus Section 4.1 begins by introducing inflation, and so functions as a prospectus for both this Section and Section 5. Section 4.2 discusses the conjectured mechanisms for it, and Section 4.3 presents this Section's main point about scientific realism: that the details of the mechanism are seriously under-determined by the data.
4.1. The idea of an inflationary epoch
As mentioned in Section 1: from about 1980 onwards, cosmologists have proposed that there was a very early (and so brief!) epoch of very rapid, indeed accelerating, expansion. They have made three main claims about this epoch: claims which will dominate this Section and the next, so that we give them mnemonic labels.
(Three): Such an epoch solves three problems faced by the existing Big Bang model, which by 1980 was well-established (it had already been dubbed "standard" by Weinberg (1972: 469) and Misner et al. (1973: 763)). These problems are the "flatness", "horizon" and "monopole" problems.
(Inflaton): If this epoch was appropriately caused - viz. by a conjectured inflaton field - it would lead to characteristic features of the CMB: namely, characteristic probabilities for the amplitudes and frequencies of the slight wrinkles (unevennesses) in the CMB's temperature distribution.
(Branch): This mechanism for inflation would naturally involve a branching structure in which, during the epoch, countless spacetime regions branch off and themselves expand to yield other universes; so that the whole structure is a "multiverse", whose component universes cannot now directly observe/interact-with each other, since they are causally connected only through their common origin in the very early universe.
The evidence for, and status of, these three claims varies. Most cosmologists regard claim (Three) as established: i.e. there was an epoch of accelerating expansion (however it may have been caused) and the occurrence of this epoch solves the flatness, horizon and monopole problems. But cosmologists agree that the cause of this epoch - its mechanism: the dynamical factors that started it, and then played out so as to end it - is much more conjectural; and therefore, so also is the third claim, (Branch). 14 The original proposal was that the mechanism was a scalar field, ϕ, the inflaton field, evolving subject to a certain potential V(ϕ); and that this mechanism led to characteristic features of the CMB. It is testimony to the strength of this proposal that it remains the most popular mechanism, and there remain versions of it which are confirmed by the CMB data. But this mechanism, and so the claim (Inflaton), is undoubtedly more speculative than the mere occurrence of the epoch of expansion. So we must beware of the ambiguity of the word "inflation": it can refer either to the epoch of expansion (also called "inflationary epoch"), however it was caused; or to the (more speculative) mechanism for its occurrence. Finally, the idea that the mechanism for inflation spawns many universes, i.e. claim (Branch), is even more speculative.
We will now concentrate on the least controversial claim, (Three): i.e. the claim that there was an inflationary epoch (however it was caused) and that such an epoch solves the three problems-flatness, horizon and monopole-faced by previous general relativistic cosmological models. Then Sections 4.2 and 4.3 take up claim (Inflaton), about what caused the inflationary epoch. And Section 5 will take up claim (Branch), about the multiverse.
4.1.1. An inflationary epoch solves three problems
The way in which an inflationary epoch solves the three problems has already attracted philosophical discussion (e.g. Earman (1995: Chapter 5, especially 142-159), Earman and Mosterin (1999: Sections 4-7, 14-26), Smeenk (2013: Section 6, 633-638), Butterfield (2014: Section 4.1-4.2, 65-67), McCoy (2015)). This is not least because two of the three problems are problems, not so much of the empirical adequacy of general relativistic cosmology, as of explanation - a natural topic for philosophers.
Thus, cosmology's established model in the mid-1970s has two features, each of which looks like an implausible coincidence that cries out for explanation. In both respects, the model is empirically adequate: the feature in question does not contradict observations. But the feature requires an aspect of the model that is otherwise free, i.e. not constrained by theory, to be fine-tuned to an extreme degree, on pain of empirical inadequacy. The simplest and clearest example is the flatness problem, where the aspect concerned is a theoretically central parameter about the spacetime geometry; and it has to be fine-tuned to many decimal places. So we shall give some details about that; then we will mention how similar considerations apply to the horizon and monopole problems.
According to the Big Bang models of the 1970s (based on the Friedmann-Robertson-Walker (FRW) metric), there are three main possibilities for the fate of the universe. Either:
(i): the universe's matter and radiation is on average dense enough that gravitation will eventually overcome the expansion, so that the universe is fated to reach a point of maximum size and then "turn around", i.e. contract and end in a Big Crunch (and of course: the greater the density, the sooner will the turn-around and Crunch occur): (called a closed universe); or
(ii): the matter and radiation density is low enough that gravitation cannot overcome the expansion, though it slows the rate of expansion down to some asymptotically non-zero value: (called a open universe); or
(iii): the matter and radiation density is (a) low enough that gravitation cannot overcome the expansion, but (b) high enough that it slows the rate of expansion down, asymptotically, to zero: (called a flat universe, since the spatial geometry of the instantaneous spatial slices is asymptotically Euclidean).
Obviously, (iii) i.e. flatness is theoretically privileged. For this value of the density represents the boundary between the regimes (i) and (ii). So the important dimensionless number is the ratio - which is written as Ω - of the actual density to this critical value. So Ω = 1 corresponds to flatness.
According to the FRW models, if Ω is ever 1, then it is always 1. And in fact, the observed value of Ω is close to 1. The universe is now, and indeed at all times later than about one second after the Big Bang, almost flat: its spatial geometry is almost Euclidean. But in these models, any difference of Ω from 1 in the early universe is very rapidly amplified. For example: if at one second after the Big Bang, Ω = 1.08, then already at ten seconds Ω = 2; and thereafter Ω keeps increasing exponentially. And on the other hand: if at one second after the Big Bang, Ω = 0.92, then already at ten seconds Ω = 0.5; and thereafter Ω keeps decreasing exponentially. In short: Ω = 1 represents an equilibrium - but a very unstable equilibrium. And this means that for Ω to be about 1 today requires that it be stunningly close to this privileged value soon after the Big Bang: for example, it has to be 1 ± 10−16 at one second after the Big Bang. 15
Should this degree of fine-tuning be treated as a "coincidence": i.e. a brute fact, set aside from the quest for explanation? Agreed: it is in general a matter of judgment, not dictated by the scientific context, what facts it is legitimate to treat as brute. But in this case: the fine-tuning is so extreme that it cannot be dismissed as brute.
And the idea of an inflationary epoch promises to predict and-or explain Ω being close to 1. For it is easy to show that whatever the value of Ω at the onset of the inflationary epoch, Ω will be driven close to 1 by the end of the period, and will remain close to 1 for a very long time thereafter-including until now. (So the explanation is dynamical: in philosophers' jargon, causal.) Besides, the idea of this explanation is very simple: an expansion of a highly curved surface makes a local patch flatter. Think of blowing up a balloon; or how the fact that the earth is large makes our local patch of it seem flat (e.g. Guth 1997: 176-177; Liddle 2003: 99, 104; Serjeant 2010: 27-28, 56).
The horizon problem has a similar structure. Namely: our cosmological description (as of the late 1970s) is empirically adequate, but requires an aspect - in this case, an initial condition - to be fine-tuned to an extreme degree: so extreme that it is implausible to treat it as a brute fact. Recall that the CMB, dating from the decoupling (recombination) time tdec (380,000 years, or about 1013 seconds), is very homogeneous and isotropic. Its wrinkles are minuscule: their proportional size is 10−5, which is like having, on the surface of a pool of water one meter deep, a wave only a hundredth of a millimeter high! Yet for two directions in space with a sufficient angular separation, the two past events at the time tdec that lie along those directions , i.e. the two emission-events of the CMB, have-according to the 1970s' models-no common causal past. That is, their past light-cones do not intersect. In the notation of Section 2.3, calling the events p, q ∈ M: I−(p) ∩ I−(q) = ∅. This means there can be no process of thermalization or equilibration - or any kind of interaction - establishing the strong correlation in the properties of the CMB coming from the different directions. The strong correlation must just be accepted as a brute fact. This is all the more embarrassing when one calculates that the angular separation sufficient to imply no common causal past is tiny: about 2 degrees. 16
Again, the idea of an inflationary epoch solves the problem: and in a simple way. Namely: a suitable inflationary epoch implies that the past light-cones of all emission events of the CMB - even for points on opposite sides of the sky - do in fact intersect; and so there could have been a suitable process of equilibration. In this way, the uniformity of the CMB, even on opposite sides of the sky, is explained: (e.g. Guth 1997: 182-186; Liddle 2003: 102, 109; Serjeant 2010: 53, 55).
Turning to the monopole problem: this is a problem of empirical adequacy, rather than a problem of having to treat as brute what seems to need an explanation. It also differs from the flatness and horizon problems in being a matter of detailed, albeit speculative, physics, rather than spacetime geometry. Namely: there is good reason to think that at sufficiently high energies (and so: sufficiently early times) the strong and electro-weak forces are unified, in the same sort of way that classical electromagnetism à la Maxwell unifies electric and magnetic forces; (recall snapshot (D) in Section 3.1). Theories of this unification, which began to be formulated in the 1970s, are called "GUTs" (for "Grand Unified Theories"). The problem is that GUTs, applied to the very early universe, predict the production of very many magnetic monopoles: these are particles that have a magnetic charge, broadly analogous to the familiar electric charge. But these particles have never been detected: a matter of contradiction with observation (rather than embarrassment at treating a fact as brute).
As to how an inflationary epoch solves this problem: the idea of the solution is attractively simple, as it was for the flatness and horizon problems. Namely: (i) one accepts that the magnetic monopoles are produced, thus not questioning the admittedly speculative physics; but (ii) the enormous expansion occurs after, or at worst during, monopole-production, so that the expansion vastly dilutes the monopoles. Thus in the tiny pre-inflation patch that expanded to become the observable universe, there would be so few magnetic monopoles that we would not expect to have detected them. 17
So much by way of presenting the three problems; and the simple underlying ideas of the solutions given by an inflationary epoch. This discussion prompts the question: how much inflation? That is: how much expansion of the universe, involving how much acceleration-and when-makes the three solutions come out quantitatively correct?
Of course, each problem prompts a separate calculation of how much expansion, and when, would be sufficient for the solution. Needless to say, each calculation involves auxiliary assumptions, which can be questioned. But the calculations are also partly independent of each other: so the fact that the resulting estimates agree pretty well is evidence in favor of an inflationary epoch. We of course cannot give details of such calculations. We just report the consensus that all three solutions come out quantitatively correct, if we postulate figures like the following (dizzying though they be!):
(a): the inflationary epoch ends at about 10−34 seconds: which is a time corresponding to GUT-scale energies, viz. E ≈ 1015 GeV (so that the temperature T = E / kB ≈ 1028 K);
(b): the inflationary expansion is exponential: and started at, for example, 5 ×10−35 seconds with a characteristic expansion time (i.e. the time in which the scale factor - the radius of the universe - is multiplied by e ≈ 2.7) of about 10−36 seconds.
Taken together with (a), this would imply expansion by a factor e50 ≈ 1022! (For further details, cf. e.g. Liddle 2003: 106-7; Serjeant 2010: 55.)
Let us sum up this Subsection's discussion of claim (Three). It is generally agreed that postulating an inflationary epoch, occurring in a suitable time-interval and increasing the size of the universe by suitably many orders of magnitude, solves the flatness, horizon and monopole problems. All three solutions invoke a satisfyingly simple idea so as to explain the puzzling feature in question. Besides, these solutions are resilient, in that they are independent of what might have caused the inflationary epoch ... but of course, one still asks: what caused that epoch?
4.2. What caused the accelerating expansion?
In answering this question, the first thing to stress is that we are here in the realms of speculation: recall Weinberg's warning in footnote 14! We shall confine ourselves to reporting a "minimal" answer: which postulates a scalar field, ϕ, the inflaton field, evolving subject to a certain potential V(ϕ) - cf. claim (Inflaton) at the start of Section 4.1. As we will see, a few assumptions about this mechanism yields some characteristic predictions for subtle features of the CMB. And since these features have been observed by a sequence of increasingly refined instruments (such as the satellites COBE, WMAP and Planck mentioned at the start o Section 3), these confirmed predictions are nowadays regarded as a more important confirmation of inflation, than its solution of Section 4.1.1's three problems. There is, however, a very considerable under-determination of the mechanism of inflation by our data - both today's data, and perhaps, all the data we will ever have. This (unfortunate!) predicament will be the topic of Section 4.3. (Then in Section 5 we will turn to the most controversial claim (Branch), that inflation yields a multiverse of domains.)
We begin with a simple classical picture of inflation, postponing
quantum considerations to Section 4.2.2. We begin
by assuming that at approximately 10−35 seconds after
the Big Bang, the stress-energy of the universe was dominated by that
associated with some (yet to be discovered) scalar field
ϕ(t,
), known as the
inflaton; and that the evolution of this scalar field is
determined by a potential energy density V(ϕ), and by its
coupling to the gravitational field.
We also assume that the dynamics of the scalar field is very simple, as
follows. The scalar field is homogeneous: i.e., the same throughout
space, so that the field is then only a function of time,
ϕ(t,
) ≡
ϕ0(t).
18
And the potential has a single minimum towards which the field `rolls':
much as a classical particle would roll towards the minimum of a
potential, subject to a force in the direction of the negative of the
potential's gradient.
It turns out that accelerating expansion of the underlying spacetime can
occur when the potential energy density dominates over the kinetic
energy of the inflaton field: i.e. V(ϕ0)
>> [1/2]
20(t) : a regime called the
slow-roll of the inflaton. In a bit more detail: what one
requires for accelerating expansion is a fluid with a pressure P
that is negative; more specifically, P < −[1/3] ρ,
where ρ is the energy density of the fluid. For the scalar field
above (which can be thought of as a fluid in this sense), where
V(ϕ0) >> [1/2]
20(t), the pressure P
comfortably satisfies this constraint.
Inflation comes to an end when the inflaton finds its way to the minimum of the potential; typically, the slope of the potential gets larger, and the kinetic energy of the inflaton increases so that accelerating expansion can no longer occur. The inflaton oscillates (with a decaying amplitude) around the minimum of the potential, and the stored energy is released into particles of the standard model of particle physics through a process known as reheating.
Although this is just one means through which the universe can expand by the amounts needed to solve the three problems discussed in Section 4.1.1, taking this slow-roll scenario seriously - that is, analyzing single-field slow-roll inflationary models, and deducing observational parameters - has hitherto been cosmologists' predominant way of exploring and assessing the idea of inflation.
4.2.2. Connecting the inflaton to the CMB
If this was all there was to the theory of inflation, it would probably not have the following amongst cosmologists that it does today. Arguably the most impressive success of the inflationary paradigm is its providing a mechanism for understanding the origin of subtle features of the CMB. The setting for this success is a quantum treatment of the (putatively classical) story sketched in Section 4.2.1; and it to this connection between the inflaton and the CMB that we now turn.
The basic observable associated with the CMB is the intensity of
radiation as a function of frequency and direction in the sky
(Hu and Dodelson 2002).
To a very good approximation, the CMB has a black-body
spectrum with an average temperature of
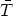∼ 2.73 K
(∼ −270.42 degrees C). But the temperature is not exactly
uniform across the sky; there are small fluctuations about this mean on
the order of 10−5 in size. That is: given the
temperature T(θ, ϕ) for a given direction (θ,
ϕ) in the sky, we subtract the mean temperature
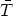and define a
dimensionless temperature anisotropy
 |
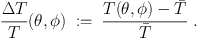(4.1) |
It is this quantity that is about ± 10−5 for any direction (θ, ϕ). By expressing it with spherical harmonics (the analogue for the surface of a sphere, of elementary Fourier series for functions on a real interval), we can represent how the size of these irregularities in T vary with angular scale. Of course, we expect the exact variation with direction in the sky, and with angular scale, to be a matter of happenstance: so we must adopt a statistical approach. So we postulate an ensemble of possible temperature functions T(θ, ϕ), equipped with a probability distribution. We then use the distribution to calculate various means (averages) and dispersions (spreads), which we compare with experiment.
The upshot of this is that for each positive integer l, a number Cl encodes the mean size of irregularities on an angular scale of about 180 deg / l. Thus l = 1 corresponds to being hot in one direction and cold in the opposite direction. Indeed, there is such a contribution, thanks to the Doppler effect due to the Earth's motion relative to the CMB (with the hot direction corresponding to shorter wavelengths, i.e. motion towards the CMB). The set of the Cl is called the angular power spectrum.
Of course, this statistical approach makes various assumptions, albeit defeasible ones: such as that the temperature fluctuations are Gaussian, which means that the angular power spectrum completely determines the statistics of the fluctuations. There are also other subtleties about the power spectrum such as (i) acoustic oscillations which are also a function of angular scale, and (ii) anisotropies associated with polarization effects in the CMB: but we will set these aside (for a discussion, see Baumann and Peiris 2009). Thus the issue at hand is how these anisotropies in temperature form, and what determines their statistics.
Inflationary cosmology proposes that these anisotropies come from small perturbations in the inflaton field, arising from its quantum fluctuations: perturbations which can then be connected (via the appropriate transfer function) to the angular power spectrum of the CMB. It is a remarkable story, spanning a complex sequence of cosmological events: but one worth briefly describing since it represents the predominant way of thinking about the origin of CMB anisotropies. (We set aside the issue of the quantum-classical transition: cf. (4) at the end of Section 1.)
The proposed mechanism is that as the (homogeneous) inflaton
ϕ0(t) rolls down the inflaton potential, it
acquires spatially dependent quantum fluctuations δϕ(t,
)). These
fluctuations mean that inflation will end at different points of space
) at different
times; and this leads to fluctuations in energy density after the end of
inflation, ultimately giving rise to fluctuations in CMB temperature as
a function of position in the sky.
The fluctuations in the inflaton field are computed in quantum theory. One can compute a power spectrum of scalar (inflaton) fluctuations, Ps(k) (here expressed as a function of the Fourier wavenumber k), whose scale (k) dependence is summarized by the scalar spectral index ns. If ns = 1 then the power spectrum is scale-invariant, whereas ns ≠ 1 encodes deviations from scale invariance. These perturbations also lead to the generation of primordial gravitational waves (i.e. tensor fluctuations), for which an analogous power spectrum can be computed. It is designated by Pt(k), for which a similar tensor spectral index nt can also be defined. The relative strength of tensor to scalar perturbations is an important cosmological parameter, and is measured by the tensor-to-scalar ratio: r : = Pt(k∗) / Ps(k∗), measured at a particular reference scale k∗.
From these power spectra for scalar and tensor fluctuations, one can infer angular power spectra for temperature and for polarization in the CMB; and conversely, measured power spectra in the CMB can be used to infer primordial power spectra. In particular, the scalar spectral index ns and the tensor-to-scalar ratio r are commonly used to constrain single-field slow-roll inflationary potentials. Recent Planck data [Ade et al. (Planck Collaboration) 2015] finds that:
(i) ns = 0.968 ± 0.006 (i.e., primordial fluctuations are nearly scale invariant), at a 68% confidence level; and
(ii) r < 0.11, at a 95% confidence level.
Thus inflation - even its simpler, single-field slow-roll, models - indeed provides potentials that are consistent with the statistics of the CMB. But how many such single-field slow-roll models are consistent with CMB measurements? It is to this question, and the underlying under-determination that its answer reveals, that we now turn.
The fact that inflation provides a mechanism for understanding both (i) very large-scale homogeneous features of our universe (Section 4.1) and (ii) much smaller-scale inhomogeneities apparent in the CMB (Section 4.2), suggests that inflationary models should be highly constrained. Indeed, they are. But there remains a wide variety of possible inflationary models which yield these impressive successes. And this variety is not a mere matter of (a) margins of error, or (b) simplicity: like a case where a physical field, e.g. a potential function, can be ascertained either (a) only within certain bounds, or (b) only by assuming it is simple in some precise sense (e.g. being a polynomial of degree at most four). Instead, inflationary models that differ by substantially more than matters (a) and (b) yield predictions that are the same-at least, the same so far as we can confirm them.
Agreed: one might hope that this under-determination is not a problem with the theory of inflation per se, but only a reflection of the effective nature of the theory. That is: although primordial inflation operates at very high energies (∼ 1016 GeV), it is expected to be some low-energy limit of a fundamental theory whose details are yet to be worked out (Cheung et al., 2008): and which will, one hopes, overcome the under-determination. Be that as it may, we now give some details about the wide variety of possible inflationary models.
Broadly speaking, inflationary model building is pursued along three main avenues: in terms of:
(i) a single scalar field (as outlined in Section 4.2.1); or
(ii) multiple scalar fields (known as"multi-field inflation"); or
(iii) non-scalar degrees of freedom.
As in Section 4.2, we shall focus on (i), and on models where the scalar field is minimally coupled to gravity: which is presumably, the simplest means of realizing inflation.
First, the good news. Such models predict negligible non-Gaussianities in the CMB, and are thus promising candidates for providing a description of the state of the very early universe. And some of them disagree with each other as regards some observations we may indeed be able to make. For example: one can categorize such models according to the range of field values ∆ϕ through which the inflaton rolls (down the potential), between the the time when the largest scales now observed in the CMB were created, and the end of inflation. When this range ∆ϕ is smaller than the Planck scale, ∆ϕ < MPl, we say there is "small-field inflation" ; whereas large-field inflation occurs when ∆ϕ > MPl. One observational difference between these two categories is the size of the primordial gravitational waves they predict: large-field inflation (but not small-field inflation) predicts gravitational waves that we may indeed be able to see in the near future.
But there is also bad news: that is, a worrying plethora of models. In a bid to understand the various possibilities for inflationary models, Martin, Ringeval and Vennin (2014a) have catalogued and analyzed a total of 74(!) distinct inflaton potentials that have been proposed in the literature: all of them corresponding to a minimally coupled, slowly-rolling, single scalar field driving the inflationary expansion. And a more detailed Bayesian study (Martin et al., 2014b), expressly comparing such models with the Planck satellite's 2013 data about the CMB, shows that of a total of 193(!) possible models - where a "model" now includes not just an inflaton potential but also a choice of a prior over parameters defining the potential - about 26% of the models (corresponding to 15 different underlying potentials) are favored by the Planck data. A more restrictive analysis (appealing to complexity measures in the comparison of different models) reduces the total number of favored models to about 9% of the models, corresponding to 9 different underlying potentials (though all of the "plateau" variety). To sum up: although this is an impressive reduction of the total number of possibilities, there remains, nevertheless, an under-determination of the potential by the data: an under-determination that is not a mere matter of (a) margins of error, or (b) simplicity, of the kind noted at the start of this Section. And of course, we have not surveyed the other avenues, (ii) and (iii) above, through which inflation might be implemented: let alone the rival frameworks mentioned in footnote 13.
Agreed, and as we said at the start of this Section: one can hope that this under-determination will be tamed as theories are developed that describe the universe at energy levels higher than those at which inflation putatively operates. But-as we shall discuss in Section 5 - this regime of yet higher energies may yield another, perhaps more serious, problem of under-determination: a problem relating to distance scales that far outstrip those we have observed, and indeed, those that we will ever observe.
13 But we stress at the outset that inflation remains a speculation, and that there are various respectable alternatives. For maestri being skeptical about inflation, we recommend: Ellis (1999, p. 706-707; 1999a, pp. A59, A64-65; 2007, Section 5, pp. 1232-1234), Earman (1995, pp. 149-159), Earman and Mosterin (1999), Hollands and Wald (2002), Penrose (2004, pp. 735-757, Chapters 28.1-28.5), Steinhardt (2011), and Ijjas et al. (2013); though we of course also recommend replies, such as Guth et al. (2014). For reviews of some alternatives, such as string gas cosmology, cf. e.g. Brandenberger (2013), or, aimed at philosophers, Brandenberger (2014). Back.
14 Thus Weinberg says: "So far, the details of inflation are unknown, and the whole idea of inflation remains a speculation, though one that is increasingly plausible" (2008: 202). Back.
15 For these numbers, cf. Guth (1997: 25), or Liddle (2003: 100). Note that 10−16 is about the ratio between the width of a human hair (viz. a tenth of a millimeter) and the average distance between Earth and Mars (viz. 225 million kilometers)! And of course, for times earlier than one second, the fine-tuning is to yet more decimal places. Back.
16 Embarrassment at having to accept strong correlation as a brute fact echoes the intuitive plausibility of Reichenbach's Principle of the Common Cause: which is much discussed as a motivation for the locality assumptions in Bell's theorem (cf. Ruetsche, this volume). For more about this comparison, cf. e.g. Earman (1985: Chapter 5), Butterfield (2014: Section 4.2). Back.
17 Our description of the monopole problem is so brief that it may be misleading: but a detailed description inevitably leads into the issue of what caused the inflationary epoch, i.e. claim (Inflaton) which we have postponed to Section 4.2. For a superb popular account, by one of the inventors of inflation, cf. Guth (1997: Chapter 9, 147-165). A detailed account of inflation's solutions to all three problems can be found in Kolb and Turner (1990: Section 8.1-8.2) and Linde (1990: Section 1.5-1.7). Back.
18 Agreed, you might object that assuming homogeneity undercuts the claim to have solved the horizon etc. problems. But in reply: there is active research to ascertain how much homogeneity is needed to secure inflation (Brandenberger (2016), East et al. (2015), Kleban and Senatore (2016)); and anyway, we aim in this essay only to lay out the main ideas. Back.