


Stars are formed within molecular clouds, vast aggregations of molecules residing in the galactic disks. These clouds that often contain the mass of a million stars, are much denser and colder than the surrounding interstellar gas. Stars are born out of the collapse of small condensation areas that are scattered throughout the much larger volume of a molecular cloud. The collapse can occur due to random density fluctuations or be externally triggered, e.g., by shockwaves from supernovae or galaxy collisions. Soon after the collapse begins, a small pressure-supported protostar at the very center of the collapse flow develops. During the main collapse phase, the central protostar is surrounded by an inward flow of gas and dust. As the protostar evolves both the temperature and the density increase inside. Finally, the central core of the protostar heats up so much that nuclear "burning" is initiated and the star begins its energy production through nuclear fusion.
Star formation is a process complicated by the details of cloud fractionation, rotation, turbulence, and magnetic fields. While the formation of low-mass stars (below 8 solar masses) is thought to be understood and proceeding through an accretion disk, the mechanism to form more massive stars is not quite understood as well. Due to the larger radiation pressure of their emissions, the accretion disk would be blown away. The current model assumes, consistent with observations, the formation of a directed jet, transporting a small fraction of material but clearing a cavity through which most of the radiation can escape without interaction with the accretion disk (Bannerjee and Pudritz 2007). In this way, low-mass and high-mass stars could be formed in a similar manner. Other models assume coalescence of two or more light stars or competitive accretion of a low- and a high-mass star feeding from the same molecular cloud (Bonnel et al. 1997; Bonnel and Bate 2006).
The galactic mass distribution of the newborn stars is known as the initial mass function. To sustain nuclear burning in their interiors, stars must have at least 8% of the mass of the Sun. During their formation, stars with a smaller mass do not release sufficient gravitational binding energy to heat the gas to temperatures required for igniting nuclear fusion. These are called brown dwarfs. The lower-mass stars between about 8 and 40% of the mass of our Sun are called red dwarfs, because of their small size and their low surface temperature. At the other end of the mass range stars more than 100 times as massive as the Sun are highly unstable due to spontaneous pair production of electrons and positron from plasma interactions and therefore do not exist in our Universe. During their enormous life spans, stars produce energy through nuclear fusion and shine continuously over millions to billions of years. Lower-mass stars consume their fuel very quietly and survive for several billion years. Massive stars, on the other hand, burn out in a few millions of years.
Stars undergo drastic changes during their evolution. One of the best methods for charting the course of stellar evolution is the Hertzsprung–Russell (HR) diagram shown in Fig. 8, a particular type of graph developed in the early twentieth century by the astronomers Hertzsprung and Russell. In this diagram, the luminosity or energy output of a star is plotted on the vertical axis, and the surface temperature of the star on the horizontal axis. For historical reasons, the surface temperatures along the horizontal axis are plotted backward, so that they increase toward the left. In the HR diagram the various stars are then plotted according to their luminosity and surface temperature. As one can see, the stars are not distributed randomly in the HR diagram, but are rather grouped in certain areas.
Most of the stars line up along a well-defined band on the HR diagram known as the main sequence and are therefore also called main-sequence stars. This trend is no coincidence. Stars that lie along the main sequence have the proper internal configurations to support fusion of hydrogen to helium. Since stars spend most of their lifetime in this hydrogen burning state, most stars in the HR diagram are lying on the main-sequence band. Our Sun is also a typical main-sequence star.
After the hydrogen supply in the core of the star is exhausted and converted to helium, the central temperature is too low to fuse helium into heavier elements. Therefore, the core lacks an energy source and cannot support anymore the overlying bulk of the star. Through the gravitational pressure, the size of the core shrinks and the temperature of the central region increases accordingly. The heat released by the core increases steadily the luminosity of the star. Paradoxically, even though the helium core is shrinking, the radius of the star, determined by the outer hydrogen layer, increases by factors of 100 to 1,000. Through this expansion, the surface temperature drops by as much as 50% and the star becomes redder. Therefore, these stars are called red giants and are found in the HR diagram in the upper right corner.
When the core temperature of the red giant reaches about one hundred million degrees, a new sequence of nuclear reactions called helium burning begins in the core where helium nuclei fuse to carbon and oxygen. Our Sun has lived for 4.5 billion years and has already burnt half of its hydrogen in the core. After about another 5 billion years our Sun will also become a red giant and will thereby increase its size so much that the radius of the Sun will reach about the Earth's orbit.
The further evolution of a star and the nature of its stellar death depend on the initial mass. If the initial mass of a star is less than about 8 solar masses, it is burning He in an unstable way (see also Sect. 4.3) and the resulting pulsations lead to the loss of huge quantities of hot gases toward the end of its life. This cloud moving away from the star is called a planetary nebula. The central small and hot core of the star that is left over is a white dwarf and consists of the ashes of helium burning, i.e., carbon and oxygen. Even though the surface temperature of the white dwarf is still very hot its luminosity is small, because nuclear fusion has ceased. Therefore, the white dwarfs are found in the lower left corner of the HR diagram.
If the initial mass of a star is more than about 8 solar masses further burning phases will take place. These are called advanced burning phases and consist of carbon, neon, oxygen, and silicon burning, being named after the nuclei mainly destroyed in that phase. In these subsequent burning phases, heavier and heavier nuclei are built up, and the ashes of the preceding burning phases provide the fuel for the subsequent burning phases. However, in the outer and therefore cooler and less dense regions of the star the previous burning phases are still continuing. This leads to shell burning with distinct adjacent shells of different chemical compositions, in which different burning phases prevail. In the outermost shell of the star still hydrogen is burnt into helium (hydrogen burning), in the next shell helium to carbon and oxygen (helium burning), and finally, in the fully evolved star, there follow still carbon, oxygen, neon, and silicon burning shells (Fig. 9). In the core of the star significant amounts of iron are accumulating through silicon burning. A detailed discussion of the nuclear burning phases is given in Sects. 4.2 through 4.4.
A detailed introduction to stellar evolution is given in the following books: Clayton (1984), Hansen and Kawaler (1994), Kippenhahn and Weigert (1994), Phillips (1994), Tayler (1994). Books and reviews discussing stellar nucleosynthesis are Rolfs and Rodney (1988), Arnett (1996), Thielemann et al. (2001b). Tables of nuclear reaction rates and cross sections can be found in Rauscher and Thielemann (2000).
The endpoint in the evolution of stars with more than 8 solar masses is a type II supernova. One should not confuse novae with supernovae and even the two types (i.e., type I and type II) of supernovae are quite different. It will become evident in the following that the sites of these explosive events are only loosely related, despite the similarity in the name. There is a major difference in the underlying mechanism between type I (SN I) and type II supernovae (SN II). The confusing choice of names is, once again, historical. Astronomy is guided by observations and early astronomers did not have the equipment to investigate the objects in any detail. Obviously, even today, it is impossible to view the events in binary systems directly. Much more detail can be seen in light curves (i.e., brightness as a function of time) and spectra.
Historically, the comparatively frequent novae (see Sect. 5.2) were named first. Subsequently, much brighter eruptions of light were observed in the sky. Since they are brighter by more than a factor of 106, they were appropriately termed supernovae. The light curve of a supernova is somewhat different from that of a nova: its rise time is only a few hours instead of days and it exponentially decays after having reached its peak. Closer investigations showed that several classes of supernovae can be found, according to features in their spectra: type I do not show hydrogen lines, whereas they are found in type II eruptions. This indicates whether the exploding object has an extended hydrogen envelope (such as massive stars). A more detailed classification scheme is shown in Table 2. Type Ia supernovae are further discussed in Sect. 5.3, while the unique scenario producing all other types (SNIb,c; SNII) is shortly introduced in the following.
| Characteristic explosion energy (1044 J) and light curve | ||||
| No H lines | H lines | |||
| Si lines | No Si lines | Exponential decay of light curve | Plateau feature in light curve | |
| He lines | No He lines | |||
| White dwarf disruption | Core collapse (binary system?) | Core collapse (binary system?) | Core collapse | Core collapse |
| SN Ia | SN Ib | SN Ic | SN II L | SN II P |
When the stellar core becomes dominated by iron, the fusion into heavier elements does not lead to the release of energy, but rather requires absorption of energy. (See, e.g., Fig. 7.13 in Chap. 7, Vol. 1, showing the cross section of the stability valley of nuclei with iron at its lowest point.) Therefore, the core lacks an energy source and is unable to support itself against gravity anymore leading to a collapse of the star. In a single second the innermost regions are compressed to nuclear densities of about 1012 kg/m3 and temperatures of about 1011 K. The iron nuclei, which have been synthesized just before in silicon burning are broken up again into protons and neutrons through the high-energy thermal radiation. The innermost regions are compressed so much that the core density becomes sufficiently high for electrons and protons to combine, producing neutrons and neutrinos. As the collapse continues, this giant ball of neutrons generally reaches a state of maximum density, and then bounces back. The bounce drives an extraordinarily powerful shock wave outward through the outer parts of the star. Investigations within the last 3 decades have made it clear that this prompt shock will not have enough energy to explode the remaining outer layers of the star. Only with the additional supply of energy through neutrino heating can the shock wave be supported to blow apart the star completely. This powerful explosion can explain supernovae of type II, but also of type Ib,c. At the center of the supernova explosion, the dense core of neutrons may be left behind as a neutron star. Alternatively, if the remaining core becomes heavier than a few solar masses through partial fallback of material, it can even collapse into a black hole. The dual explosion mechanism with prompt shock and delayed explosion by neutrinos is still not understood well. A proper treatment of the neutrino transport requires detailed three-dimensional hydrodynamic simulations, which are currently beyond the capability of modern computers and thus one has to refrain to approximations whose merits are debatable. For an overview, see, e.g., Janka et al. (2007).
The physics of the remaining compact objects after stellar death, e.g., white dwarfs, neutron stars, and black holes are discussed by Shapiro and Teukolsky (1983).
4.2. Hydrogen Burning : Proton–Proton Chain, CNO-Cycle
For nuclear reactions to take place in the interiors of stars, a temperature of at least 10 million degrees is necessary. This high temperature is needed because nuclei have positive charge and therefore repel each other through the Coulomb potential. The typical kinetic energy of nuclei in stellar interior range from between a few keV to a few 100 keV being much smaller than the typical height of a few MeV of the Coulomb barrier between reaction partners. Therefore, nuclear reactions in stars proceed mainly by barrier penetration exploiting the quantum mechanical tunnel effect. The cross sections decrease exponentially with the kinetic energies of the nuclei because of the decreasing penetration probability through the Coulomb barrier. The dependence on the relative kinetic energy E between interacting nuclei can be represented most simply by a formula in which a factor proportional to the inverse of the relative kinetic energy 1/E and the barrier penetration factor G(E) is factored out from the cross section: σ(E) = (1/E) G(E) S(E). This leaves a function S(E) called the astrophysical S-factor that varies smoothly with the kinetic energy E of the interacting nuclei in the absence of resonances. Neutron-induced reactions would not have to overcome the Coulomb barrier. However, neutrons are not very abundant in stellar interiors. They still play a major role for the nucleosynthesis of heavy nuclei through the so-called s- and r-processes, to be discussed in Sect. 4.5.
The reaction rate, expressed as the number of reactions per volume and per time, is proportional to the astrophysical S-factor. At the temperatures and densities relevant to the stellar environments the interacting nuclei have a Maxwell distribution of speeds. This distribution has also to be taken into account when determining the reaction rate. An introduction to astrophysical S-factors and reaction rates can be found in many textbooks on nuclear astrophysics, e.g., Arnett (1996), Rolfs and Rodney (1988), Iliadis (2007), Boyd (2008).
Nuclear burning in late hydrostatic phases (see, e.g., silicon burning) and in different explosive scenarios proceeds at high temperatures and densities. This leads to equilibrium between forward and reverse reactions, e.g., capture and photodisintegration. It gives rise to equilibrium abundances depending only on the supply of free neutrons and protons and on certain nuclear properties. High temperatures favor the creation of light nuclei because photodisintegration processes dominate. High densities lead to heavy nuclei, and intermediate conditions yield the highest abundances for nuclei with high binding energies. Such an equilibrium can be established within a group of nuclear species where individual reactions link different groups. This is called quasi-statistical equilibrium (QSE). The full nuclear statistical equilibrium (NSE) is reached when all nuclei are equilibrated.
In the following, the different burning stages will be described one by one, starting with hydrogen burning, being the first burning stage of every star.
In hydrogen burning, occurring in the cores of main-sequence stars like our Sun, ordinary hydrogen nuclei (i.e., protons) are burnt through a chain or cycle of nuclear reactions into 4He nuclei. In this stellar plasma there are two processes burning hydrogen: the proton–proton chain (pp-chain) (Fig. 10).
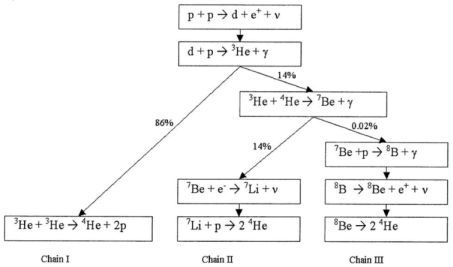 |
Figure 10. proton-proton chain of hydrogen burning. |
The pp-chain proceeds through a sequence of two-body reactions. The first reaction in the pp-chain is the exothermic fusion of two protons p into the deuteron d consisting of a proton p and a neutron n through the reaction
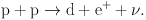 |
(2) |
For this reaction to take place a proton p must be converted into a neutron n through p → n + e+ + ν, releasing a positron e+ and a neutrino ν. Such a conversion can only proceed through the weak interaction (see Sect. 3.1). Therefore, the rate of the reaction in Eq. (2) is very low, which makes the reaction the bottleneck of the pp-chain.
Once the deuteron d is formed, it very rapidly undergoes the reaction
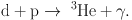 |
(3) |
There are two alternatives for the next step, leading to a branching of the pp-chain into the ppI- and ppII-chain. In the ppI-chain, occurring in 86% of the cases, two 3He nuclei fuse to a final 4He nucleus while two protons are released:
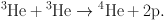 |
(4) |
In the ppII-chain, occurring in 14% of the cases, a 3He nucleus fuses with a 4He nucleus creating a 7Be nucleus and thereby releasing a photon, γ:
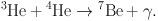 |
(5) |
In almost all cases, this reaction is followed by the capture of an electron and emission of a neutrino ν, thereby converting a 7Be nucleus into 7Li. This is followed by the capture of another proton, creating two 4He nuclei:
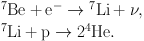 |
(6) |
Another branching into the ppIII-chain occurs in a very small percentage of cases with a total probability of only 0.02%. In this chain, reaction (5) is followed by the following sequence of reactions:
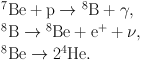 |
(7) |
The net reaction of all three pp-chains
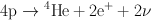 |
(8) |
leads to a transformation of four protons into a 4He nucleus releasing two positrons e+, two neutrinos ν and a total energy of 26.73 MeV. A fraction of this energy is carried away by the neutrinos, which leave the star practically unhindered due to their negligible interaction with the solar material.
Fusion of hydrogen into helium may also be achieved through another sequence called CNO-cycle (Fig. 11), which is notably different from the pp-chain:
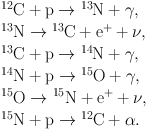 |
(9) |
In this sequence the C, N, and O nuclei only act as "catalysts" and the net reaction of the CNO-cycle is again given by Eq. (8).
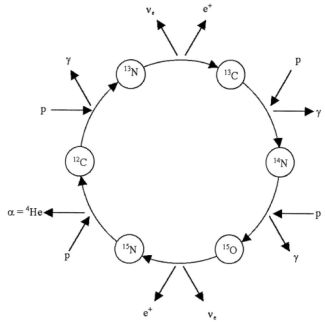 |
Figure 11. The carbon, nitrogen, and oxygen (CNO)-cycle of hydrogen burning. |
For main-sequence stars lighter than about 2 solar masses, the pp-chain dominates in hydrogen burning, whereas the CNO-cycle is favored over the pp-chain in stars that are more than twice as massive as the Sun.
In our Sun the pp-chain dominates over the CNO-cycle, producing about 98% of the total energy. A prerequisite for CNO-cycles is, of course, the existence of the elements C, N, O in the stellar plasma. Stars formed early in the Galaxy (first-generation stars) contain only primordial elements and thus are not able to burn hydrogen through a CNO-cycle at all.
The Sun's temperature in the core is about 1.5 × 107 K, whereas the surface temperature is only about 5,600 K. The Sun has already lived for 4.6 billion years, and will have enough hydrogen supply to live for about another 5 billion years. This leads to a long lifetime of about 10 billion years before its fuel is exhausted.
How can information be obtained from the Sun's core, where hydrogen burning takes place? The photons reaching us from the Sun are emitted from the solar surface. They have changed their energy enormously by many scattering processes on their way from the hot solar core to the relatively cool surface of the Sun. Therefore, in the visible region only the solar surface and not the solar interior can be observed. One possibility to obtain information about the Sun's core is helioseismology, i.e., by observing the vibration modes of the Sun. It was confirmed through helioseismology that our standard solar model is correct (Fiorentini and Ricci 2000; Bahcall et al. 2001a; Christensen-Dalsgaard 2001).
Another possibility is to observe the neutrinos that are set free in nuclear reactions of the pp-chain and CNO-cycle and reach the surface practically unhindered. Presently four neutrino detectors measuring solar neutrinos exist: HOMESTAKE (USA), GALLEX (Italy), (SUPER)KAMIOKANDE (Japan), and SNO (Canada). All these neutrino detectors are underground in order to shield out the cosmic rays that would give unwanted background signals in the neutrino detectors. The existing solar neutrino detectors measure only about 1/3 to 1/2 of the electron neutrino flux compared to the value calculated from the standard solar model (Bahcall 2000). This discrepancy is called the solar neutrino problem (Bahcall 1989, 1999). Possible problems both with the neutrino measurements and with our standard solar model have been ruled out. Recently, at SNO it was possible to observe not only the solar electron neutrinos, but also the μ- and τ-neutrinos in the same experiment (Heger 2001; SNO Collaboration et al. 2002a, b). The measured total neutrino flux agrees with the value expected from the standard solar model. The solution to the solar neutrino problem implies some new physics by the introduction of the so-called neutrino oscillations Neutrino oscillations (see Sec. 8.2 in Chap. 10, Vol. 1). Through such oscillations, the electron neutrinos ν emitted in the solar core by the nuclear reactions given in Eqs. (2), (6), and (7) can change into other types of neutrinos. Thus, mainly μ-neutrinos emerge on their way from the core of the Sun to the detector. Experiments measuring electron neutrinos thus show a smaller flux than initially emitted in the solar core (Bahcall 2001; Bahcall et al. 2001b; Fiorentini et al. 2001). This physical picture is the culmination of about 40 years of solar neutrino detection and research.
Recently, these findings have been combined with the results of the so-called atmospheric neutrino anomaly, where μ-neutrinos generated in pion decays oscillate over into, mainly, τ-neutrinos. In addition, terrestrial experiments performed with neutrino fluxes (produced either at nuclear power plants or with accelerators) provide substantial information on the mixing pattern among the different neutrino species. Searches for possible oscillations into further light neutrino flavors, which would be of clear cosmological significance, have not yet provided a clear answer to the question of their existence. (See Sect. 8.2 in Chap. 10, Vol. 1).
4.3. Helium Burning : Nucleosynthesis of Carbon and Oxygen
The fusion of protons into helium continues until the star has exhausted its hydrogen. When this happens, the star undergoes a gravitational collapse and the temperature rises to about a few times 108 K in the core of the star, which makes the fusion of helium into heavier nuclei possible. In the first reaction of helium burning, the fusion of two 4He nuclei creates the 8Be nucleus. However, the 8Be nucleus has an extremely short mean life of only 10-16 s, before it decays back again to two 4He nuclei. This process is in equilibrium, where the rate of production equals the rate of destruction of the 8Be nucleus:
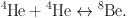 |
(10) |
The 8Be just produced can, however, capture another 4He nucleus creating the 12C nucleus through the reaction
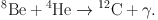 |
(11) |
The reactions (10) and (11) are called the triple-α reaction, because three 4He nuclei or α particles are necessary for the creation of 12C. This reaction can only create carbon in appreciable amounts because of the existence of a resonance in 12C at the relevant energy for helium burning. Through this resonance, reaction (11) is enhanced by many orders of magnitude.
In helium burning, about half of the carbon nuclei produced are converted to oxygen nuclei 16O by the capture of another 4He nucleus:
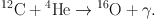 |
(12) |
Further captures of helium nuclei 4He by oxygen nuclei 16O occur only to a much lesser extent and therefore helium burning comes to an end after the creation of 12C and 16O.
Carbon and oxygen are the two most important elements for carbon-based life. Carbon is needed for the complex nuclei of the DNA and proteins, whereas oxygen is needed even for water. Interestingly enough, these two elements are extremely fine-tuned with respect to the nuclear force. If the strength of this force were 0.5% larger or smaller, the average abundance of carbon or oxygen in our Universe would be reduced by more than two orders of magnitude. This would make the existence of carbon-based life in our Universe very improbable (Oberhummer et al. 2000; Schlattl et al. 2004).
Outside the stellar core burning helium, hydrogen burning continues in a shell around the core. If the initial mass of a star is less than about 8 solar masses no more burning phases will take place after helium burning and nuclear burning stops. A white dwarf with a surrounding expanding planetary nebula will be the endpoint of the star's life. Charbonnel et al. (1999) and Marigo (2001) review the chemical yields in light and intermediate-mass stars between 0.8 and 8 solar masses.
Two interesting effects happen in helium burning of low-mass stars. Firstly, stars with less than about 2 solar masses undergo a core He flash instead of igniting stable He burning after the H burning phase. This is because the cores of lower-mass stars are more dense than those of higher-mass stars. For stars with less than about 2 solar masses, the contracted He core is so dense that it cannot be described as an ideal gas. Rather, it is a degenerate gas, in which pressure is only depending on density but not on temperature. Once the triple-α reaction, being very efficient at high density, is ignited, a thermonuclear runaway ensues because the rising temperature does not raise the pressure and therefore does not cause an expansion of the burning zone. Thus, the usual self-regulation mechanism of hydrostatic burning is not working anymore and He burning proceeds quickly to high temperature. Very high temperatures lift the degeneracy of the gas and its equation-of-state becomes temperature dependent again very suddenly. This causes an explosive expansion of the outer core, also ejecting the outer layers of the star as a planetary nebula.
The second phenomenon occurs in stars between 2 and 8 solar masses, the so-called Asymptotic Giant Branch (AGB) stars. Regular He burning takes place in the core of these stars in their red giant phase. With the exhaustion of He in the center of the star, the burning zone moves outward and becomes a burning shell. Thus, there are two shells burning, a H-burning shell and a He-burning shell. The He-burning shell is very thin and does not generate sufficient energy to balance the mass layers on top of it through radiation pressure. This squashes the shell more and more. Because of the nonlinear dependence on density of the triple-α rate, which is actually two reactions one after another, the energy release will considerably increase but still not be enough to expand and self-regulate the shell against the pressure from the surrounding layers. Further contraction enhances the triple-α rate nonlinearly and so on. Although the gas is not degenerate, a similar thermonuclear runaway as in the degenerate case occurs. When a critical temperature is reached, enough energy is released to expand the shell explosively against its surroundings. This rapid expansion, the He-shell flash, is so strong that it also blows out the H-burning shell. Due to the expansion, the density drops and the triple-α reaction ceases. Quickly, the star contracts again, the outer material settles, and first the H-burning shell and then the He-burning shell is ignited again. This sets the stage for another such cycle. AGB stars undergo a large number of such pulses, where the thermonuclear runaway phase with the flash lasts only a few hundred years whereas the time between pulses is a hundred to a thousand times longer. Oscillations and vibrations are induced into the stellar plasma by these pulses, leading to increased mass loss from the surface of the star. AGB stars have strong stellar winds, which considerably decrease their total mass during their evolution. The shell flashes have another important impact: they cause large convection zones, mixing the plasma constituents across large distances within the star. This is important for the production of the s-process nuclei (see Sect. 4.5.1).
He-shell flashes only occur in low-mass stars because they are caused by thin He-burning shells and the size of the shells scale with the stellar mass.
In a massive star with more than 8 solar masses, the next stage after helium burning is carbon burning. This starts when the carbon/oxygen core has shrunk so that the temperature at its center has reached about 5 × 108 K. Then two carbon nuclei fuse together creating 20Ne or 23Na nuclei:
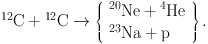 |
(13) |
The next stage is neon burning starting at 109 K, in which photons first disintegrate 20Ne and liberate 4He, which in turn reacts with the undissociated 20Ne to build up 24Mg and further nuclei:
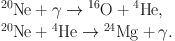 |
(14) |
Oxygen burning occurs when the temperature reaches 2 × 109 K, the most important reaction being the one producing 28Si:
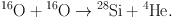 |
(15) |
The final stage is reached at a temperature of 5 × 109 K, when silicon burning begins. At this high temperature, a series of reactions takes place beginning with the photodisintegration of 28Si:
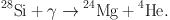 |
(16) |
Then the released 4He nuclei build up heavier nuclei by successive capture reactions
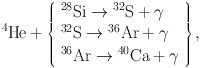 |
(17) |
and so on. At such high temperatures, capture and photodisintegration reactions are in equilibrium. In this so-called nuclear statistical equilibrium (NSE) the knowledge of individual reactions or reaction rates is not important anymore to calculate the abundances. The produced abundances only depend on the temperature and density of the plasma and the nuclear binding energies (Iliadis 2007; Boyd 2008). The result of this series of photodisintegration and capture reactions is the steady buildup of heavier elements up to the elements grouped around iron (Hix and Thielemann 1998), with 56Ni preferentially produced because it is the nucleus with the highest binding energy and having equal number of protons and neutrons.
T he sequence of stellar burning is terminated when the core of the star is largely composed of elements in the mass region of nickel and iron, because no more energy is to be gained from further nuclear reactions. As soon as the energy produced is not enough to maintain the hydrostatic equilibrium, the core cannot support the outer layers anymore, and it begins to collapse due to its gravitation, leading to a core-collapse supernova (see Sect. 4.1.3).
In a core-collapse supernova explosive nucleosynthesis also takes place through the outward proceeding shock wave (Thielemann et al. 2001a), modifying the elemental abundance pattern of the outer layers of the pre-supernova star. This explosive burning of the C-, Ne-, O-, and Si-layers in the star mainly leads to modifications of the abundances in the region from Ca to Fe (Rauscher et al. 2002). Photodisintegration of heavy nuclei also leads to the production of proton-rich stable nuclides, the so-called p-nuclides (see also Sect. 4.5.2). The strong neutrino emission caused by the formation of a neutron star in the core collapse influences nucleosynthesis in the deepest, barely ejected layers of the star as well as in the outer layers (Sects. 4.5.2 and 4.5.3).
Nucleosynthesis of massive stars is reviewed by Rauscher et al. (2002), Woosley and Heger (2007). An overview of stellar nucleosynthesis including hydrogen, helium, neon, silicon, and explosive burning as well as the basics of the s- and r-process are given by Rauscher and Thielemann (2001). Explosive burning and the s- and r-processes are also introduced below.
4.5. Nucleosynthesis Beyond Fe
As it has been seen in the preceding sections, stellar burning phases only lead to the production of nuclei up to Fe. A review by National Research Council of the National Academies identified 11 key questions to be addressed in science in the next decade (Turner et al. 2003). Ranked three on the list is "How were the elements from Fe to U produced?" Although the ground to answer this question has been laid by Burbidge et al. (1957), Cameron (1957) and much progress has been made since then, there remain a number of problems regarding the astrophysical sites of certain nucleosynthesis processes and also concerning the properties of certain, highly unstable nuclei in such processes. In the following subsections, a brief summary is given of the current knowledge of how elements beyond Fe were synthesized.
The Main and Weak s-Process Components
Due to the lack of a Coulomb barrier, the most likely process for the formation of elements heavier than those grouped around iron is neutron capture. If a supply of neutrons is available, they can accrete by sequential neutron captures on a "seed nucleus" in the region of iron to build up neutron-richer nuclei. As the neutron number of the nucleus increases, it will become unstable to β- decay, transforming a neutron into a proton in the nucleus, and emitting an electron and an antineutrino. Successive neutron captures, interspersed by β- decays build up many, but not all of the heavier stable nuclei.
There are two basic timescales in this scenario of heavy-element nucleosynthesis by neutron captures: (1) the β-decay lifetimes, and (2) the time intervals between successive captures that are inversely proportional to the neutron capture reaction rates and the neutron flux. If the rate of neutron capture is slow compared to the relevant β decays, the synthesis path will follow the bottom of the stability valley very closely. On the other hand, if the rate of neutron capture is faster than the relevant β- decays, highly neutron-rich nuclei will be formed. After the neutron flux has ceased, those nuclei will be transformed to stable nuclei by a series of β- decays. The above two processes are called s- and r-process, respectively, according to their slow or rapid rate of neutron capture. The observed abundances of nuclei in the solar system, especially in the regions of closed-shell nuclei, suggest that the s- and r-processes contributed more or less equally to the formation of the elements above the iron region (see Fig. 12).
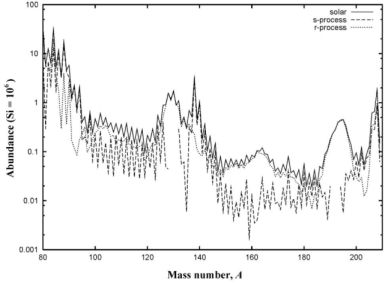 |
Figure 12. Contribution of s- and r-process to the solar abundances of the isobars for heavy elements (p-isotopes cannot be seen in this figure because of their very small abundances). Solar system abundances are measured (Anders and Grevesse 1989), s- and r-abundances are calculated. The peaks in the solar abundances around mass numbers A = 88, 138, 208 are formed in the s-process, whereas the broader companion peaks shifted to slightly lower mass number are r-process peaks. |
Two important reactions provide neutrons for the s-process:
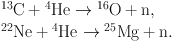 |
(18) |
The reaction on 13C is much more efficient in releasing neutrons because it is strongly exothermic, as opposed to the second reaction. However, 13C normally does not occur in He-burning zones whereas 22Ne does. This proved to be a longstanding problem in complete stellar simulations of s-process nucleosynthesis.
Early observations (see Burbidge et al. 1957) had already found Tc on the surface of AGB stars. Since Tc isotopes are short lived compared to the age of such a star, they had to be produced in that star and brought up to the surface. Only in recent years, sophisticated stellar models were able to follow the complicated convection and nucleosynthesis processes inside AGB stars with sufficient accuracy to confirm them as the production sites. He-shell flashes (see Sect. 4.3) and the mixing brought about by them turned out to be the key (Busso et al. 2001; Boothroyd 2006). Such a flash can mix down protons from the unburnt outer layer of the star, which can then be used to produce 13C by proton capture on 12C and subsequent β-decay of the resulting 13N. With this 13C neutrons can be very sufficiently released even during the interpulse phase. Additionally, the reaction on 22Ne can release further neutrons during the high temperature phase of the flash itself. Thus, the nuclides in the stellar plasma are irradiated with neutrons in bursts over millennia. The large convection zones appearing in the flash phase bring up the newly synthesized material to the surface.
In the manner described above, AGB stars produce the majority of the s-process nuclei, the so-called main component. It was known for a long time that there must be a second site of s-processing, producing light s-nuclei. Because they exhibit smaller abundances than those of the main component, this was called the weak component. Such a weak s-process is found in massive stars (i.e., stars with more than 8 solar masses), where capture of 4He by 22Ne is the main neutron source. Massive stars reach higher temperatures than AGB stars already in their late evolution stages, which help to release neutrons. Even more neutrons can be released during explosive burning, when the temperature rises due to the supernova shock wave passing through the outer layers of the star. Because of the inefficiency of the 22Ne neutron release and the short timescale, this mechanism cannot proceed much beyond Fe in massive stars.
For nucleosynthesis of the heavy elements through the s-process in both AGB and massive stars, there already must be nuclei present in the iron region, which were produced in previous generations of stars. Thus, the s-process will be stronger in stars formed more recently than in older stars containing less heavy elements.
Explosive Nucleosynthesis in the Outer Layers of a Massive Star
Since the buildup of nuclei in the s- (and r-) process follows the neutron-rich side of the stability valley (see, e.g., Fig. 13 in Chap. 7, Vol. 1), 32 proton-rich isotopes cannot be produced in either process. These so-called p-nuclides occur naturally but with abundances many orders of magnitude lower than the other nuclides. The hypothetical process synthesizing these nuclides was termed p-process and several models have been suggested. The commonly favored one is photodisintegration of preexisting nuclei in the Ne/O shells of massive stars. When a supernova shockfront is passing through these layers, the high temperatures of 2–4 GK enable photodisintegration, starting with γ-induced emission of several neutrons, leading to proton-rich nuclei. The photodisintegration path can branch when proton or α emission becomes more favorable than neutron emission in such proton-rich nuclei. The bulk of p-nuclides can be explained in such a model but some problems remain (Rauscher et al. 2002; Arnould and Goriely 2003; Boyd 2008). Especially the production of the light p-isotopes, in particular 92,94Mo and 96,98Ru, is not understood. Among the p-nuclei they have by far the highest abundance but cannot be produced concurrently with the others. It remains an open question whether the stellar models have to be revised or an additional production mechanism has to be invoked for these light p-nuclei.
The neutrino flux of a core-collapse supernova is high enough to contribute to the nucleosynthesis of certain rare elements and isotopes, even in the outer layers of the star. In this so-called ν-process, inelastic scattering of a neutrino leads to formation of an excited daughter nuclide, which then decays by particle emission. This process can contribute significantly to the production of light (11B, 19F) and heavy (138La, 180Ta) nuclides (Woosley and Weaver 1995; Heger et al. 2005).
Explosive Burning in the Deep Layers of a Massive Star
In addition to s-process nucleosynthesis, about half of the nuclides beyond Fe are produced through rapid neutron captures on short timescales in the r-process. The site of the r-process is controversial. Mostly favored are core-collapse supernovae where appropriate r-process conditions are thought to be found close to the region of neutron star formation. These innermost layers, which are barely ejected, move outward within a strong neutrino flux, driving the material to become very neutron rich. With a high neutron density, neutron captures can proceed much faster than β-decays and produce very neutron-rich nuclei far from stability. Through simultaneously occurring captures, photodisintegrations with neutron emission, and β-decays, heavier elements are synthesized within a few seconds. When the ejected material cools down, those highly unstable nuclei decay back to stability, thus supplying the needed fraction of heavy elements. While the s-process is confined to the region up to Bi, the r-process is thought to also reach the region of fissionable nuclei and produce natural, long-lived elements such as U. The endpoint of the r-process path is highly debated since it depends on fission barriers of very neutron-rich, heavy nuclei, for which there is no consensus among theoretical models yet.
The conditions in those innermost regions of a core-collapse supernova are closely linked to the working of the explosion mechanism. Since the latter is not yet fully understood, it is not yet clear whether the required conditions can actually be established. Therefore, a number of alternative scenarios are still discussed, such as jet outflows from asymmetrically exploding stars. The search for the site of the r-process remains a major focus of research.
Recently, an additional nucleosynthesis process in the deep layers of the exploding star has been suggested (Fröhlich et al. 2006). It was discovered that the combined flux of neutrinos and antineutrinos from the emerging, hot neutron star initially creates very proton-rich conditions before the matter becomes neutron rich at later times and/or larger radii. The high temperature and density environment gives rise to rapid proton captures, thus synthesizing nuclei beyond Fe but on the proton-rich side of stability. A small number of neutrons are required to speed up the matter flow to heavier elements and these are produced by antineutrino captures on protons. The νp-process could perhaps explain the surprisingly high abundance of Sr, Y, and Zr found in very old stars (Travaglio et al. 2004; Frebel et al. 2005). Again, the details of this so-called νp-process (including the question of how efficiently it can produce elements beyond Fe) depend strongly on the conditions in the deep layers of the exploding star and the explosion mechanism. Among the suggested alternative scenarios are wind outflows from the accretion disks around black holes formed by core collapse of very massive stars (Surman et al. 2006). These are also thought to be the cause of so-called γ-ray bursts, which are the most energetic phenomena observed in our Universe today (MacFadyan and Woosley 1999; Mészáros 2006).
4.6. Nucleosynthesis by Spallation
The light and fragile elements lithium, beryllium, and boron (LiBeB) are not primarily produced in primordial or stellar nucleosynthesis. In fact, the abundance curve in Fig. 13 shows a huge dip (almost a gap, actually) for the mass numbers 8–11, reflecting the scarcity of LiBeB-nuclei in the solar system. Only the nuclide 7Li can be produced both in primordial (see Sect. 3) and in stellar nucleosynthesis (see Sect. 4.2), whereas the nuclides 6Li, 9Be, 10B, and 11B are almost pure spallation products of heavier elements.
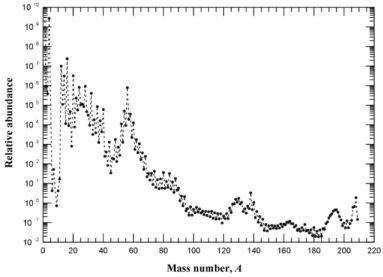 |
Figure 13. Relative solar abundances by mass number. Data are from Anders and Grevesse (1989). The abundances are arbitrarily renormalized to yield a value of 106 for silicon |
The high-energetic galactic cosmic rays (GCRs) originate probably from supernovae (Erlykin and Wolfendale 2001). GCRs consist mainly of fast-moving bare hydrogen and helium nuclei and, to a lesser amount, of carbon, nitrogen, and oxygen nuclei (CNO)-nuclei. Hydrogen and helium nuclei of interstellar clouds can spall the CNO-nuclei in flight of the fast GCRs. Therefore, the GCRs are by about a million times enriched in LiBeB-nuclei compared to the solar system abundance.
The most plausible origin of the main bulk of LiBeB-nuclei is that hydrogen and helium nuclei of GCRs hit and spall CNO-nuclei contained in interstellar clouds. However, this process alone seems unable to produce LiBeB at the observed level. Therefore, another production site of LiBeB-nuclei has been proposed. This invokes in-flight fragmentation of carbon and oxygen nuclei by collision with hydrogen and helium nuclei in interstellar clouds. The sites of this process are mainly the surroundings of massive stars, which are able to furnish freshly synthesized carbon and oxygen nuclei and accelerate them via shock waves. Finally, spallation through neutrinos in supernova explosions also produces the nuclides 7Li and 11B (Hartmann et al. 1999).
A review of nucleosynthesis by spallation is given by Vangioni-Flam et al. (2000).