


Since the quark–hadron phase transition no free quarks or gluons exist anymore. The hot plasma is composed of neutrons, protons, electrons, positrons, photons, and the electron-, muon-, and tau-neutrinos and their antineutrinos. Basically, all particles with masses 2m < k T / c2 are present because the respective particle–antiparticle pairs can be created in photon collisions. Scattering reactions thermalize all plasma constituents to the same temperature and forward and reverse reactions are in equilibrium. For instance, protons can be converted into neutrons by electron capture e– + p ↔ n + νe, neutrons into protons by positron capture e+ + n ↔ p + νe. While all other constituents are highly relativistic, the nucleons are slower due to their large mass. Their kinetic energy exhibits a Maxwell–Boltzmann distribution appropriate for the given plasma temperature. Although formation and destruction reactions are in equilibrium, protons will be more abundant because of their lower mass. The ratio of neutron to proton number densities only depends on the temperature and the mass difference Δm between the nucleons as long as the reaction equilibria apply (Börner 1988; Kolb and Turner 1990; Peacock 1999):
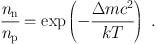 |
(1) |
Once kT ≤ 1 MeV (i.e., at about 1010 K), the electrons are not energetic enough anymore to overcome the mass difference between neutrons and protons in electron captures. Also, photons cannot produce positrons anymore in pair-production processes to support positron capture on neutrons. Such weak transitions will thus cease to exist. Since the neutrinos were produced in such reactions, thermal communication of the neutrinos with the other constituents comes to an end. This phase is called weak freeze-out and weak decoupling because the neutrinos become decoupled from the rest of the particles and can assume different temperatures. Since there is little, if any, interaction between this neutrino background and the remaining particles, its evolution is governed predominantly by the expansion rate of the Universe similar to the photon background radiation after electromagnetic decoupling that gives rise to the cosmic microwave background (see Sect. 2.1.1). Thus, in addition to the cosmic microwave background there is a cosmic neutrino background stemming from the era of weak decoupling. Its temperature is lower by a factor of 0.714 because of the heating of the photons by e+ – e- annihilation after weak decoupling.
With the ceasing of electron and positron capture, the ratio of neutrons to protons gets frozen at the decoupling temperature, yielding a value of about 1/6. However, after the weak freeze-out, photons still dominate the total energy of the Universe and thus the temperature is decreasing as the inverse square root of the time, according to the law valid for a radiation-dominated Universe. The ratio between baryon and photon number densities η = nb / nγ characterizes a particular solution of the equations for the expanding early Universe and, therefore, the solutions can be labeled by the parameter η (Kolb and Turner 1990; Coles and Lucchin 1996; Riotto and Trodden 1999). Assuming a globally valid η, the baryon density can be written as a function of temperature: ρb = 3.376 × 104 η T93 g cm-3 (T9 is the temperature in units of 109 K.) In fact, η is inversely proportional to the total entropy of the Universe, which has to remain constant.
Together with the equation for the evolution of the temperature T9 = 13.336 / t1/2, this sets the conditions for primordial nucleosynthesis. The strength of the standard Big Bang scenario is that only one free parameter – the above-introduced baryon-to-photon ratio η – must be specified to determine all of the primordial abundances ranging over 10 orders of magnitude.
The parameter η also depends on Ωb = ρb / ρc, i.e., the ratio of the baryon density to the critical density ρc needed for a flat Universe.
Thus, a fit of η to observed primordial abundances not only probes the conditions in the early Universe at the time of nucleosynthesis but can also reveal the curvature of the Universe, or at least the baryonic contribution to that curvature (Schramm and Turner 1998). Historically, primordial nucleosynthesis was the first tool for determining the geometry of the Universe. With the increased accuracy in the resolution of the angular multipole expansion of the CMBR temperature fluctuations delivered by WMAP, the total density of the Universe (and not just the baryonic one) can be determined independently now (see Sect. 2.1).
3.2. The Reaction Network and the Production Process of Nucleosynthesis
After the weak freeze-out, the baryonic matter part essentially consists of free neutrons and protons interacting with each other. Deuterium is constantly formed via neutron captures on protons. However, due to the low binding energy of the deuteron the created deuterons will preferably be destroyed by photodisintegration as long as the (photon) temperature is higher than 109 K. Below that temperature, photodisintegration is no longer effective, and more heavy elements can be built up by further reactions on the deuterons. Thus, although free neutrons and protons had already existed earlier, the onset of further primordial nucleosynthesis is delayed until about 2 s after the Big Bang (Boesgaard and Steigman 1985; Bernstein et al. 1991).
Because free neutrons are not stable, but decay with a half-life of T1/2 = (10.25 ± 0.015) min, the neutron-to-proton ratio will change from 1/6 to 1/7 until the onset of primordial nucleosynthesis.
While the Universe expands further, it cools down and the decreased energy of the photons cannot prevent significant formation of deuterons anymore. Thereafter, heavier nuclides can be created by reactions involving protons, neutrons, and the newly formed nuclear species (Schramm and Turner 1998; Sarkar 1996). This is nothing else than a freeze-out from a high-temperature, low-density nuclear statistical equilibrium (NSE), similar to the one occurring in late and explosive phases of nucleosynthesis (see Sects. 4.4 and 4.5) but at different density. An NSE is defined by all reactions via the strong and electromagnetic forces being in equilibrium. The equilibrium abundances are then only determined by the (baryon) density, the temperature, and the binding energy of the nuclei, as well as by the initial composition of the material, i.e., the neutron-to-proton ratio. The latter is set by the weak freeze-out and the subsequent neutron decay. In a high-temperature NSE, all nuclei are completely dismantled into their constituents: the protons and neutrons. Assuming a quick freeze-out in such a manner that late-time nonequilibrium reactions will not significantly alter the NSE abundances, the resulting abundances can already be determined without detailed reaction network calculations. With decreasing temperature, simply the most strongly bound nuclei at the given neutron-to-proton ratio will be formed. Thus, mainly unprocessed protons and 4He nuclei are expected to be present, which exhibit a high binding energy, with all neutrons having been incorporated into the 4He nuclides. Formation of elements beyond He is hindered by the fact that there are no nuclei with mass numbers 5 and 8. The 3α reaction (see Sect. 4.3) could convert 4He to 12C but is not in equilibrium because it is strongly dependent on the density and too slow at the conditions in the early Universe. Nuclei close to 4He are produced according to their binding energies.
The important reactions and the produced nuclear species are shown in Fig. 4. The conditions at the onset of and during the nucleosynthesis are given by the initial values and parameters discussed above, with η being a free parameter.
A typical result of a full network calculation for a specific η is shown in Fig. 5 (Tytler et al. 2000; Kolb and Turner 1990). As can be seen, practically no nucleosynthesis occurs during the first 2 s, the temperature remains above 1010 K, and no other nuclides than free nucleons are favored. Only after a sufficient drop in temperature, deuterons are formed, 3H and 3He nuclei are produced, quickly followed by 4He. The neutron abundance is determined by slow β-decay in the early phase. During the formation of 4He, the neutron abundance suddenly drops because most of the neutrons are incorporated into the α particles. Slightly delayed, traces of 7Li and 7Be nuclei are formed. During the decline of the temperature, charged particle reactions freeze out quickly and after about 15–30 min nucleosynthesis ceases. The very few free neutrons decay into protons, 3H eventually also decays and so does 7Be, which forms further 7Li. Finally, by far the most abundant species are hydrogen (protons) and helium (4He, i.e., α particles), which together give more than 99.9% of the baryonic material. Although this calculation did not assume NSE at all times, the resulting abundances are very close to the ones obtained from equilibrium abundances and fast freeze-out. Realizing the dominance of 4He due to its high binding energy, it is easy to understand that about 25% of the gas is made up of helium. The initial n/p ratio of 1/7 translates into mass fractions Xn = 0.125 and Xp = 0.875 (i.e., 12.5% of the gas mass consists of neutrons). Assuming that all neutrons combine with protons to form 4He, the mass fraction of 4He has to be Xα = 2Xn because it contains two neutrons and two protons. Thus, Xα = 0.25, i.e., 25%.
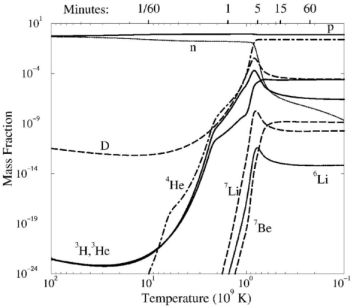 |
Figure 5. Primordial abundances of different nuclear species as a function of time and temperature for a fixed ratio of baryon to proton number densities, η = 5.1 × 10-10 (Reprinted from Tytler et al. 2000 with kind permission of the first author and IOP) |
An interesting result was obtained from the fact that the initial n/p ratio depends on the weak freeze-out (see above). The freeze-out time and temperature and thus also the resulting n/p ratio depends on the change in the degrees of freedom during freeze-out (Kolb and Turner 1990). Although only three neutrino families were known originally (Nν = 3), it remained an open question for a while whether there are more families containing light (nearly massless) neutrinos. Increasing the number of neutrino species increases the number of degrees of freedom and has a similar effect to that of a faster expansion resulting from larger pressure. Thus, a larger number of neutrino families would lead to an earlier weak decoupling at a still higher temperature. This results in a higher n/p ratio and consequently leads to more 4He.
Primordial nucleosynthesis calculations performed along these lines were able to put the limit Nν ≤ 3.3, ruling out any further families long before any particle physics experiments. This was possible due to several facts: helium is very abundant and can be easily measured in astronomical observations; it is strongly bound and therefore robust during galactical chemical evolution; its abundance only weakly depends on η; the primordial production reactions are well determined; and the half-life of the neutron (determining the change of the n/p ratio between weak freeze-out and onset of nucleosynthesis) is measured to high accuracy. This prediction on the number of neutrino species was later confirmed by experiments at CERN (see the article of D. Karlen in Hagiwara et al. 2002) directly measuring the decay widths of the Z0 boson in the weak interaction.
The nuclear reaction rates (cross section) for the reactions specified in Fig. 4 are well determined, also at the interaction energies relevant to primordial nucleosynthesis, which are comparatively low by nuclear physics standards. Thus, once the initial conditions are determined, the evolution of the different species with time and the final abundances can be calculated with high accuracy. The only open parameter in the standard Big Bang nucleosynthesis model is η. Since the baryon density is proportional to η and the reaction rates are density dependent, the final abundances will also depend on the choice of η.
Fig. 6 shows this dependence for a typical range of the baryon density and equivalently its fraction of the critical density Ωb. Immediately catching the eye is the difference between the density dependences of the different species: the 4He fraction increases slightly with increasing density while the deuterium and 3He fractions strongly decrease (note that the vertical scale of the upmost curve is linear, while those of the rest are logarithmic). The simple explanation is that a high density during the nucleosynthesis phase gives rise to a larger number of capture reactions on deuterium and 3He, producing more 4He but leaving less of the targets. 7Li shows a more complex behavior with a pronounced minimum. At low densities 7Li is produced by α-capture on 3H but is preferably destroyed at higher densities by the reaction 7Li(p,α)4He. However, at higher densities the production of 7Be via 3He(α, γ)7Be also increases. This 7Be is not destroyed by any further primordial process but eventually decays to 7Li after nucleosynthesis has ceased. The different density dependences of the three main reactions involved give rise to the minimum shown in Fig. 6.
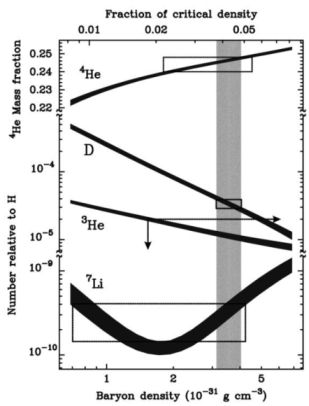 |
Figure 6. Primordial abundances as a function of baryon density ρb or fraction of critical density Ωb (these two quantities are directly related to the baryon-to-photon ratio η, see text). The widths of the curves give the nuclear physics uncertainties. The boxes specify the ranges of abundances and densities constrained by observation (there is only an upper limit for 3He from observation) as given in Burles et al. (1999, 2001). The shaded area marks the density range consistent with all observations (Burles et al. 1999, 2001). Symbol D represents deuterium, 2H (Reprinted from Tytler et al. 2000 with kind permission of the first author and IOP) |
3.3. Comparison of Calculations and Observed Primordial Abundances
Except for helium, the abundances of the primordial isotopes change by orders of magnitude when varying the baryon density or η, respectively. On the other hand, 4He is very abundant and thus it can be observed with high accuracy. Therefore, it is possible to determine η from comparison with primordial abundances. As outlined above, this means nothing less than determining the total baryon density and thus the baryonic contribution to the curvature of our Universe! The allowed abundance range for each primordial species is shown in Fig. 6, combined with the calculated baryon density. It is reassuring that the independent observations for each species still permit a consistent range of η, i.e., all the observations are consistent with the same baryon density.
Serious complications arise from the fact that the calculations have to be compared to primordial abundances, not to the ones currently found in stars or the interstellar medium (Boesgaard and Steigman 1985; Olive et al. 2000; Tytler et al. 2000; Olive 2001; Steigman 2006). During the further evolution of the Universe, when stars are formed and destroyed, the abundances within a galaxy change with time (see Sect. 6.4) due to the stellar production and destruction processes (see Sect. 4). Thus, it is not trivial to determine the primordial values, especially those for isotopes that are weakly bound and therefore easily destroyed in stars such as deuterium, 3He, or 7Li nuclei. In order to trace the effects of chemical evolution, the standard practice is to correlate the abundance of the nuclide in question with the abundance of a nuclide, which becomes monotonically enriched in the interstellar medium during the course of the chemical evolution, e.g., oxygen. This other nuclide serves as a tracer of the metallicity of an object, i.e., the content of elements beyond hydrogen and helium (a technical term borrowed from astronomy). From the observation of different sites with different metallicities, one hopes to find trends that can be extrapolated to zero metallicity, i.e., to the primordial values. Fig. 7 shows an example of such an extrapolation.
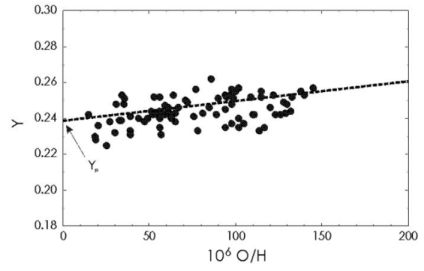 |
Figure 7. Example of the extrapolation to primordial values. The primordial value of 4He (Yp) for zero metallicity (zero oxygen) is inferred from a series of observations (filled circles) (Olive 2001). For other primordial isotopes the slope of the interpolation would be steeper, for 7Li there would be a steep rise at higher metallicities and a flat line with nearly constant abundance at low metallicity (Reprinted from Olive 2001 with permission by Springer). |
The spectra of 4He are easy to observe due to its high abundance. This He isotope can be identified in clouds of ionized interstellar gas around bright, young stars (HII regions). Although the abundance in an object can be determined with high precision, a large systematic uncertainty remains due to observations of different objects. On the other hand, the observation of 3He is difficult and an extrapolation carries a large uncertainty because different stars both produce and destroy it effectively. Due to its weak lines it cannot be seen in low-metallicity stars. The chemical evolution of 7Li is also complex but it can at least be seen in old stars. Such stars contain a factor of 0.03–0.0003 less "metals" (in astronomy: all elements except H and He) than the Sun. Studying such stars, a remarkable discovery was made: below a certain metallicity the content of 7Li remains almost constant, i.e., a plateau appears in the abundance plots. The 7Li-plateau was thought to give the primordial value. However, the question of possible depletion in early stars remains to be addressed (Korn et al. 2006) as well as the dependence of the data on the underlying assumptions, such as model atmospheres (Charbonnel and Primas 2005; Asplund et al. 2006a). These problems give rise to a large systematic uncertainty also for 7Li. Until recently, deuterium was usually observed in the local interstellar medium. However, the situation has greatly improved in recent years. It became possible to observe 2H absorption lines in quasar spectra (Tytler et al. 2000). Quasar light passes through clouds at high redshift, i.e., far away and at the same time far back in time, which contain (almost) primordial amounts of deuterium, 2H. Because of the brightness of quasars such lines can still be identified although the photons have traveled a long distance. In summary, only upper limits can be given for primordial 3He and the primordial values of 4He and 7Li have a smaller individual observational error compared to 3He but a considerable systematic uncertainty in the observations. The averaged 2H values from far objects seem to give the tightest constraint for Big Bang Nucleosynthesis (BBN) calculations (Steigman 2007).
The dependence of primordial abundances on Ωb are shown in Fig. 6. Using the available abundance information, it is found that it has to lie between about 0.038 and 0.048, also somewhat depending on the choice of the value of the Hubble constant (Schramm and Turner 1998; Burles et al. 2001; Steigman 2007). Most recently, an independent value for ηb was derived from the WMAP data of the CMBR (see Komatsu et al. 2009 for latest results). The CMBR value of ηb = (6.11 ± 0.2) × 10-10 is in excellent agreement with the value derived from the BBN abundances for 2H and 3He. Depending on improvements in the observations and theoretical models of the evolution of 4He and 7Li with metallicity, their required ηb may or may not remain in agreement with the CMBR value. However, the BBN model still is in good standing when considering the CMBR data due to the large systematic uncertainties inherent in the observations of the latter isotopes (Steigman 2007).
Assuming only baryonic matter, the small value of Ω = Ωb would indicate an open Universe, i.e., one expanding forever. However, theory of inflation demands that Ω = 1 (exactly) and thus a flat Universe (Kolb and Turner 1990; Peacock 1999). This is in agreement with the latest observations of the CMBR as discussed in Sect. 2.1.2. Then the missing mass required to close the Universe must be nonbaryonic. Indeed, there are other indications (in the initial creation and later dynamics of galaxies) that there is more gravitational interaction than can be accounted for by standard baryonic matter. Of further interest is the value of the cosmological constant (see Sect. 2.1.4), which was found to be nonzero in recent distance measurements (Perlmutter et al. 1997; Schmidt et al. 1998; Perlmutter et al. 1999; Wood-Vasey et al. 2007; Riess et al. 2007), using type Ia supernovae as "standard candles" (Sects. 2.1.4 and 5.3). The cosmological constant Λ also provides a contribution ΩΛ to the expansion of the Universe so that the new requirement reads ΩM + ΩΛ = Ωb + Ωs + ΩΛ = 1, with Ωs being the nonbaryonic contribution (Steigman et al. 2000). At the time of writing, it is not clear yet what constitutes the nonbaryonic mass. A quite general name for possible new, exotic particles is WIMP, an acronym for "weakly interacting massive particle" (see Sects. 2.1.3 and 2.1.4 for details).