© CAMBRIDGE UNIVERSITY PRESS 2000

7.4 Growth of structure: clusters, walls, and voids

We still have not answered the question that we asked at the end of Section 7.1: how did our Universe, which was highly uniform at the time of recombination, develop the galaxy clusters, and the huge walls and voids that we see in Figure 7.3? These structures are visible at the present time t₀ because the density of luminous matter in them is a few times greater than in the surrounding regions. If we assume that galaxies trace the mass density, then in the language of Equation 7.25, the fractional change in density | (t₀)| 1.

Earlier, density variations must have been far smaller. At the time of recombination, the time when matter became neutral and transparent to photons of the cosmic background radiation, its temperature was T_rec 3000 K. Since then, the radiation has been redshifted by an amount 1 + z_rec 3000/2.7 1100. Equation 7.28 tells us that if density fluctuations present at time t_rec were to develop into the clusters, walls and voids that we observe today, they must have been at least as large as (t_rec) ~ 10^-3. If the Universe has a low density, with ₀ ~ 0.1, then we would need (t_rec) 10^-2, since these structures must have reached ~ 1 by the time they stopped growing, at z ~ 1 / ₀.

What effect would variations in the matter density have on the cosmic background radiation as we observe it today? In Equation 7.27, we assumed that the perturbation refers to the total density, with the radiation and matter remaining well mixed; these are called adiabatic fluctuations. To reach us from an overdense region, radiation has to climb out of a deeper gravitational potential. In doing this, it suffers a gravitational redshift proportional to _g, the excess depth of the potential: its temperature T changes by T, where T / T ~ _g / c². If the dense region has radius R, then its excess mass M = 4 R³ /3. At these early times, the average density is very nearly equal to the critical density of Equation 7.17, so we can write

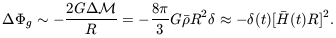
(7.40)

The dense region subtends an angle on the sky of ~ R / d_A, where d_A is the angular diameter distance, which we will define in Section 8.3. So the increment to the gravitational potential is _g /c² - ². A more careful calculation gives T / T - ² / 3; the radiation reaching us from denser regions has a lower temperature.

The Cosmic Background Explorer satellite COBE made maps with angular resolution 7° or 0.1 radians. At the time of recombination, a region of this size contains a mass ~ 10²⁰ M. The temperature variations on that huge scale were no more than a few parts in 10⁵. Extrapolating to the smaller fluctuations that were to make galaxy clusters, we have (t_rec) 10^-3 on those scales. If the density is close to the critical value, with ₀ 1, such tiny ripples are only just large enough to generate the galaxy clusters that we see today. If ₀ ~ 0.1, they are grossly insufficient. In Section 1.5 we saw that the measured amount of deuterium and other light elements implies that neutrons and protons can account for no more than ₀ = 0.1. Unless the Universe contains other forms of matter, the density fluctuations at the time of recombination are far too small to make the walls and voids that we observe today.

The difficulty might be avoided if the Universe had begun with its matter arranged in a slightly irregular pattern, but with the radiation almost completely uniform: these are isothermal or isocurvature fluctuations. They are popular with some cosmologists, but we do not know of any process that would distribute the matter in this way. Others postulate that most matter in the Universe consists of the weakly interacting massive particles, or WIMPs, that we discussed in Section 2.3. To see why WIMPs could be useful, we must ask what forces could prevent a gas cloud from becoming ever denser, as gravity draws matter inward.

Objects like stars are supported by gas pressure, which counteracts the inward pull of gravity. The larger a body is, the more likely it is that gravity will win the fight against the outward forces that hold it up. In life, the giant insects of horror movies would be crushed by their own weight. A large cloud of gas collapses if its gravitational potential energy outweighs the kinetic energy in its random internal motions and the thermal motion of its atoms. Using Equation 3.31 for the potential energy PE of a sphere of radius r filled with gas of density and sound speed c_s, we can compare it with the thermal energy KE:

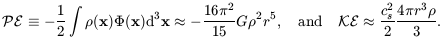
(7.41)

If we have |PE| > KE, then the cloud's diameter 2r must exceed a lower limit:

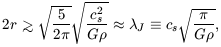
(7.42)

where the length _J is called the Jeans length. A more careful analysis shows that when gas is compressed, both its pressure and the inward force of gravity are increased. Higher internal pressure tends to cause expansion, while the the extra gravity pulls inward. If a gas cloud's diameter is less than _J, the additional pressure more than offsets the increased gravity: the cloud re-expands. In a larger cloud gravity wins, and collapse ensues.

In the early radiation-dominated phase of the Universe, the density and sound speed c_s in Equation 7.42 are those of a gas of photons: the density is _r = a_B T⁴ / c², and c_s = c / 3. So the Jeans length

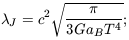
(7.43)

it grows as T^-2 or as ² (t) as the Universe expands. The Jeans mass M_J is the amount of matter in a sphere of diameter _J:

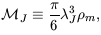
(7.44)

where _m refers only to the matter density. Since _m decreases as ^-3, the Jeans mass grows as M_J ³ (t); the mass enclosed in a sphere of diameter _J increases as the Universe becomes more diffuse. At the time t_eq when the density of matter is equal to that in radiation, the temperature was T_eq, and _m = _r = a_B T⁴_eq / c²; so we can write

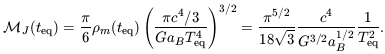
(7.45)

If equality occurs at the redshift 1 + z_eq = 24 000 ₀ h² of Problem 7.9, then at earlier times the Jeans mass can be written as

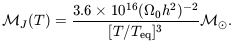
(7.46)

At the time of equality, the Jeans mass has grown much larger than the mass of a galaxy cluster: according to Equation 1.24, it is about the mass that we would find today in a huge cube (50 / ₀ h²) Mpc on a side. This is approximately the spatial scale of some of the largest voids and complexes of galaxy clusters in Figure 7.3.

Overdense regions with masses below M_J could not collapse before the time of recombination. Instead, radiation gradually diffused out of them, taking the ionized gas with it, and damping out small irregularities. By the time that the gas became neutral and transparent, matter concentrations with M 2 x 10¹² (₀ h²)^-5/4 M would be smoothed away.

The very hugest structures would also have been unable to grow. Before time t, light and gravitational influences could not propagate beyond the horizon _H (t) given by Equation 7.23. So larger structures were unable to collapse until the horizon expanded to encompass them. Until the time of matter-radiation equality, the mass of baryons within the horizon was no more than M_H (t_eq) 10¹⁵ (₀ h²)^-2 M. Variation or uniformity on larger scales must reflect conditions at early times, before the cosmic expansion had begun to follow Equation 7.20. According to the inflationary theory, quantum fluctuations in the field responsible for the vacuum energy _VAC leave their imprint as irregularities in the density of matter and radiation. After inflation ends, most versions of the theory predict that on large scales the power spectrum P(k) k, and that the random phase hypothesis, on which Equation 7.4 depends, should be valid.

By a redshift z_rec ~ 1100 when the temperature T_rec 3000 K, hydrogen atoms had recombined, and the pressure of radiation was removed. The sound speed drops to that of the matter:

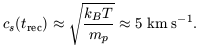
(7.47)

During recombination, the Jeans mass of Equation 7.44 falls abruptly by a factor of 10¹⁴! Just afterward, we have

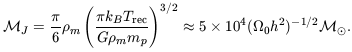
(7.48)

Radiation continues to transfer heat to the matter, keeping their temperatures roughly equal until z ~ 100. Since the radiation temperature T_rec (t), the decreasing temperature offsets the drop in density _m to keep the Jeans mass nearly constant, about equal to the mass of a globular cluster. If the first dense objects formed with roughly this mass, they could subsequently have merged to build up larger bodies. Once it is no longer receiving heat, the matter cools according to as T_m ^-2. To see why, think of the perfect gas law relating temperature to volume, or recall that expansion reduces the random speeds of atoms according to Equation 7.24. So the Jeans mass falls further; gas pressure is far too feeble to affect the collapse of anything as big as a galaxy.

If the only matter in the Universe is the `normal' matter of neutrons and protons, collectively called baryons, then Equation 7.45 tells us that only very large matter concentrations can grow at early times. These huge structures are generally not spherical; as they collapse, they shrink fastest along their shortest direction, forming a `pancake' shape (Figure 7.9). Since gas pressure is not important, collapse occurs on roughly the free-fall timescale t_ff of Equation 3.23. By Equation 6.36, compressing the gas decreases its cooling time. If it is initially dense enough to cool within the free-fall time, the cloud rapidly loses energy as it shrinks, reducing the Jeans mass. Smaller fragments of the dense pancake can then collapse successively, to become galaxy clusters and individual galaxies. Where sheets intersect, large clusters of galaxies would form. This picture is called the top-down model, since the largest structures in the Universe would be made first.

Figure 7.9. Orthogonal views of a homogeneous ellipsoid of cold gas, collapsing under its own gravity; pressure forces are neglected. The initial axis ratios are b/a = 0.7, c/a = 0.5. Time is measured in units where G = 1 and = 2 , so the final frame is at t = 1.5 x tff, the free-fall time of Equation 3.23 - J. Dubinski.

But if WIMPs accounted for most of the matter, smaller objects could collapse and become dense at an earlier stage. To see why, we can recalculate the minimum mass of a region that will collapse under its own gravity, by analogy with Equation 7.44. WIMPs are unaffected by radiation pressure. So where the density of WIMPs is _w and the random speed is c_w, a dense region would fall in on itself if it contained a mass larger than

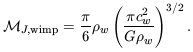
(7.49)

While the WIMPs are relativistic, their Jeans mass is high; but as soon as the speed c_w drops appreciably below c / 3, the Jeans mass starts to fall. Lumps of WIMPs with the mass of galaxies or galaxy clusters could start to collapse well before comparably sized chunks of normal matter. As it escaped from the contracting clouds of WIMPs, the radiation would have taken the normal matter with it. So both of these should be quite evenly spread at recombination, and we would expect very little variation in the temperature of the cosmic background radiation. Later, as the matter became neutral, and was freed of the radiation pressure, it would fall into the already-dense clumps of WIMPs. Fluctuations in the density of normal matter could then grow much more rapidly than Equation 7.27 would allow, building up the galaxies and clusters that we see today.

WIMPs massive enough that their sound speed c_w fell below the speed of light long before the time t_eq of matter-radiation equality are called cold dark matter. If these account for most of the mass in the Universe, then the first structures to collapse might have been of galactic mass, or smaller. Galaxies themselves would be built from these smaller fragments; at the present, each should have a massive dark halo made largely of WIMPs. We call this the bottom-up picture because galaxies form early, and then fall together to form clusters and larger structures. WIMPs with masses of only a few electron-volts remain relativistic until the time of recombination, and are called hot dark matter. They behave much like photons; the Jeans mass stays high, and we again have top-down galaxy formation.

Figure 7.10 shows results from a computer simulation, following the way that gravity amplifies small initial ripples in an expanding universe of cold dark matter. The figure shows a stage of the calculation representing the present day; note the profusion of dense small structures. The densest regions, shown in the side boxes, have ceased to expand and have fallen back on themselves. Hydrogen gas would accumulate there, cooling to form groups of luminous galaxies.

Figure 7.10. Slice 20 h-1 Mpc thick, through a cosmological simulation with cold dark matter. Density 0 = 0.4; the amplitude of the power spectrum is chosen to match the COBE measurements. Side frames show magnified views of dense clumps; galaxy groups would form in these `dark halos' - D. Weinberg.

The very large walls and voids that we see in Figure 7.3 are too big to be affected by the cold dark matter WIMPs. In bottom-up galaxy formation, matter clumps much more strongly on small scales of a few megaparsecs than on large scales. We can use models like Figure 7.10 to predict the power spectrum P(k), defined by Equation 7.3, and compare that with measured values.

The simplest inflationary theory of cosmology predicts that the Universe should be flat, with = 1 exactly. The left panel of Figure 7.11 shows the corresponding power spectrum, when we choose the parameters to reproduce the observed clustering on scales of k^-1 ~ 8 h^-1 Mpc. When the curve is scaled to agree with what is required to fit COBE's observations of the microwave background, the clustering is far too strong on the scales of a few megaparsecs that are characteristic of galaxy groups and clusters.

Figure 7.11. Power spectrum P(k) of luminous galaxies from the APM survey (filled points with error bars); boxes show constraints from fluctuations in the microwave background, measured by COBE and the Cambridge Anisotropy Telescope, CAT. Curves are for cold dark matter models, with `standard' initial fluctuations in density. Left, 0 = 1; right, 0 = 0.4 - S. Hatton.

Another approach is to decrease the assumed density of the Universe; weakening gravitational forces suppresses the clumping of the densest small-scale regions. The right panel of Figure 7.11 shows what the ₀ = 0.4 model of Figure 7.10 predicts; the peak of the power spectrum moves to larger scales, at k^-1 ~ 100 h^-1 Mpc. The smooth curve is now a fairly good match to the observed clustering of luminous galaxies. In this model, space is negatively curved. We will see in Section 8.3 that a fixed angle on the sky now corresponds to a larger linear distance, so the limits we derive from the microwave background observations move to smaller wavenumber k. The calculations do not include dissipation of energy in the normal matter, which acts to increase the density of galaxies on scales k^-1 1 Mpc; so the model curve falls below the measured power spectrum there.

A further option is to postulate that fluctuations on small mass scales were weaker to begin with: this is known as a `tilted perturbation spectrum'. This hypothesis suffers the same defect as biassed galaxy formation: nobody knows when it should happen, or how to predict its form. Some astronomers advocate a combination of top-down and bottom-up models; they postulate a mixture of hot and cold dark matter, making galaxies with the aid of the cold dark matter, and large structures with the hot dark matter. Others feel that this idea is implausibly contrived.