

| © CAMBRIDGE UNIVERSITY PRESS 2000 |
7.3.1 How do peculiar velocities build up?
When some part of the Universe contains more matter than average, its
increased gravity brakes the expansion more strongly.
Suppose that the average density is
 (t),
so that the ratio
(t),
so that the ratio  (t) =
(t) =
 /
/
 crit, and
the average expansion is described by the scale factor
crit, and
the average expansion is described by the scale factor
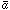 (t), and the Hubble
parameter
(t), and the Hubble
parameter 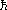 (t).
Then within the volume we are studying, we write
(t).
Then within the volume we are studying, we write
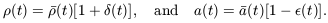
| (7.25) |
If our region is approximately spherical, we can follow the same steps that led us to Equation 7.15: the matter outside will not exert any gravitational force within it. If the region is large enough that we can ignore gas pressure (see below), then it will behave just like part of a denser, more slowly expanding, cosmos.
Where the local density exceeds the critical value, with
1 +  (t) >
(t) >
 -1 (t),
expansion will be halted, allowing
bound groups and clusters of galaxies to form. Matter will fall
in on itself, growing ever denser until pressure intervenes to arrest
the collapse, or random motions become important. Where there is less
matter than average, the expansion is faster; the region becomes
even more diffuse relative to its surroundings. Once the Universe is
matter dominated, we have (see the following problem)
-1 (t),
expansion will be halted, allowing
bound groups and clusters of galaxies to form. Matter will fall
in on itself, growing ever denser until pressure intervenes to arrest
the collapse, or random motions become important. Where there is less
matter than average, the expansion is faster; the region becomes
even more diffuse relative to its surroundings. Once the Universe is
matter dominated, we have (see the following problem)
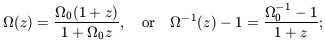
| (7.26) |
so  (t) always
approaches unity as z ->
(t) always
approaches unity as z ->  , or
t -> 0. Even if
, or
t -> 0. Even if
 0 < 1 and
the average density is now below critical, at early times only a tiny
fractional change would be required to give
0 < 1 and
the average density is now below critical, at early times only a tiny
fractional change would be required to give
 > 1.
> 1.
Problem 7.14: Use Equation 7.19 to show that
a2 H2 (t) [ 1 -
|
The problem becomes much simpler if we are in the linear regime,
where  and
and
 of Equation 7.25 are much
less than
unity. We noted in Section 7.1 (in the
discussion following
Equation 7.4) that fluctuations on scales larger than
about 8 h-1 Mpc are linear at present;
earlier, even smaller structures were in this regime. We can
substitute into Equation 7.20, ignoring
terms in
of Equation 7.25 are much
less than
unity. We noted in Section 7.1 (in the
discussion following
Equation 7.4) that fluctuations on scales larger than
about 8 h-1 Mpc are linear at present;
earlier, even smaller structures were in this regime. We can
substitute into Equation 7.20, ignoring
terms in  2,
2,

 ,
,
 2, and higher powers of
these variables. Remembering that terms involving only barred average
quantities will cancel, we find
2, and higher powers of
these variables. Remembering that terms involving only barred average
quantities will cancel, we find
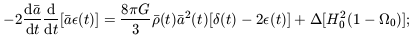
| (7.27) |
the last term represents the change in the present density and
expansion rate within our denser region. When the Universe is
matter dominated,  a3 is constant, so
a3 is constant, so
 = 3
= 3
 .
Using Equation 7.22 for
.
Using Equation 7.22 for
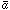 (t), we have
(t), we have
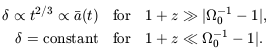
| (7.28) |
Early on, z is large and the contrast in density grows
proportionally to  (t).
At late times, when the average motion is given by
(t).
At late times, when the average motion is given by
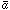
 t, matter coasts outward
with constant speed. Its gravity is too weak to have any effect on the
expansion, so
t, matter coasts outward
with constant speed. Its gravity is too weak to have any effect on the
expansion, so  remains fixed.
If we now live in a low-density
Universe with
remains fixed.
If we now live in a low-density
Universe with  0 ~
0.1, large structures ceased to
become denser around redshift z ~ 8.
If
0 ~
0.1, large structures ceased to
become denser around redshift z ~ 8.
If  0
0
 1, clusters continue to
become denser,
and voids in the galaxy distribution to expand, up to the present day.
1, clusters continue to
become denser,
and voids in the galaxy distribution to expand, up to the present day.
Problem 7.15: Substitute |
Problem 7.16: Show that |
Any denser-than-average region pulls the surrounding galaxies more
strongly toward it. While the fractional deviations
 (x, t)
from uniform density remain small, Equation 7.28 tells us that
over a given time,
(x, t)
from uniform density remain small, Equation 7.28 tells us that
over a given time,  (x)
increases by an equal factor everywhere.
Because the pull on a galaxy from each overdense region increases
in the same proportion, its acceleration, and hence its peculiar
velocity, is always parallel to the local gravitational force.
So by measuring peculiar motions, we can
reconstruct the force vector, and hence the distribution of mass.
(x)
increases by an equal factor everywhere.
Because the pull on a galaxy from each overdense region increases
in the same proportion, its acceleration, and hence its peculiar
velocity, is always parallel to the local gravitational force.
So by measuring peculiar motions, we can
reconstruct the force vector, and hence the distribution of mass.
To see how this works, we can write the velocity u(x, t) of matter at point x as the sum of the average cosmic expansion directly away from the origin, and a peculiar velocity v:
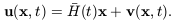
| (7.29) |
The equation of mass conservation relates the velocity field
u(x, t)
to the density, which we write as
 (x, t) =
(x, t) =
 (t)
[ 1 +
(t)
[ 1 +  (x, t)]:
(x, t)]:
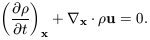
| (7.30) |
Remembering that terms involving only the barred average quantities
will cancel, and dropping terms in
 2,
2,
 v and v2,
we have
v and v2,
we have
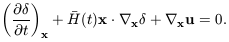
| (7.31) |
Setting x = 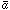 (t)
r, we switch to the coordinate r
comoving with the average expansion. The time derivative
following a point at fixed r is
(t)
r, we switch to the coordinate r
comoving with the average expansion. The time derivative
following a point at fixed r is
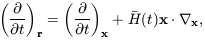
| (7.32) |
and since 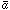 (t)
(t)
 r =
r =
 x,
Equation 7.31 simplifies to
x,
Equation 7.31 simplifies to
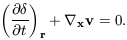
| (7.33) |
Defining a velocity potential
 v such that
v =
v such that
v =  x
x
 v, we rewrite this as
v, we rewrite this as
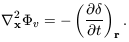
| (7.34) |
For a small enough volume, if we assume that the Universe
beyond is homogenous and isotropic, we can use Newton's laws to
calculate the gravitational force Fg corresponding to local
deviations from the average density
 , and the potential
, and the potential
 g such that
Fg = -
g such that
Fg = -

 g.
Equation 3.9, Poisson's equation, tells us that
g.
Equation 3.9, Poisson's equation, tells us that
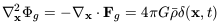
| (7.35) |
- which looks suspiciously like the equation for
 v.
Equation 7.28 assures us that all perturbations
grow at the same rate, so
v.
Equation 7.28 assures us that all perturbations
grow at the same rate, so
 (x, t)
(x, t)
 ð
ð  (x, t)
/ ð t. Then
as long as both v (x, t) and
Fg diminish to
zero as | x | increases, they
must also be proportional: the peculiar velocity is in the same direction
as the force resulting from local concentrations of matter.
Dividing the right-hand sides of the last two equations, we find
(x, t)
/ ð t. Then
as long as both v (x, t) and
Fg diminish to
zero as | x | increases, they
must also be proportional: the peculiar velocity is in the same direction
as the force resulting from local concentrations of matter.
Dividing the right-hand sides of the last two equations, we find

| (7.36) |
From Equation 7.28, in a matter-dominated Universe we have
f = 1 for 
 1, and f -> 0 as
1, and f -> 0 as
 -> 0; in general, f
(
-> 0; in general, f
( )
)

 0.6
is a good approximation.
Using Equation 3.5 for the force, we
can write the peculiar velocity as
0.6
is a good approximation.
Using Equation 3.5 for the force, we
can write the peculiar velocity as
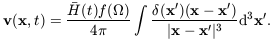
| (7.37) |
Problem 7.17: Show that if the density is uniform apart from a single
overdense lump at x = 0, then distant galaxies
move toward the origin with v (x, t)
|
Problem 7.18: In the expanding coordinate r, show that
Use Equation 7.28 for
|
So if we can measure the overdensity
 (x) of the nearby rich
galaxy clusters, and the peculiar velocities of the galaxies around
them, we should be able to test Equation 7.37
and solve for the density parameter
(x) of the nearby rich
galaxy clusters, and the peculiar velocities of the galaxies around
them, we should be able to test Equation 7.37
and solve for the density parameter
 0. First, we
determine the average peculiar motion v (x) of our galaxies.
We must assume that the Universe is homogeneous and isotropic on
even larger scales, so that forces from galaxies outside
our survey volume will average to zero. Inverting Equation 7.37
should then yield the product f
(
0. First, we
determine the average peculiar motion v (x) of our galaxies.
We must assume that the Universe is homogeneous and isotropic on
even larger scales, so that forces from galaxies outside
our survey volume will average to zero. Inverting Equation 7.37
should then yield the product f
( 0) .
0) .
 (x), from
which we can find
(x), from
which we can find  0.
0.
But the mass distributions predicted from measured peculiar velocities do not match the observed clustering of galaxies very well. Alternatively, we could say that the forces calculated from the galaxies at their observed positions do not yield the measured peculiar motions. The pull of matter outside the volume of our present surveys appears to be significant. In particular, we have still not identified the concentration of matter responsible for most of the Local Group's peculiar motion of ~ 600 km s-1. Work is under way on this problem, and galaxy surveys are being extended as techniques for finding distances improve.
Locally, we can use the crude model of
Figure 7.8 for the
Virgocentric infall to estimate the density parameter
 0.
Let dV
0.
Let dV
 16 Mpc be the distance of
the Local Group from the
center of the Virgo cluster. Within a sphere of radius
dV
about the cluster center, the density of luminous galaxies is roughly
2.4 times the mean; if the mass density is increased by the same
factor, then the overdensity
16 Mpc be the distance of
the Local Group from the
center of the Virgo cluster. Within a sphere of radius
dV
about the cluster center, the density of luminous galaxies is roughly
2.4 times the mean; if the mass density is increased by the same
factor, then the overdensity

 1.4.
Although Equation 7.36 was derived for
1.4.
Although Equation 7.36 was derived for
 << 1,
we can use it to make a rough calculation of
f(
<< 1,
we can use it to make a rough calculation of
f( ).
).
Assuming that the Virgo cluster is roughly spherical, the additional
gravitational pull on the Local Group is
Fg  4
4  G dV
G dV

 / 3,
just as if all the cluster's mass had been concentrated at its center.
So our peculiar motion toward Virgo is
/ 3,
just as if all the cluster's mass had been concentrated at its center.
So our peculiar motion toward Virgo is
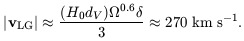
| (7.39) |
Cosmic expansion is pulling the cluster away from us at a
speed H0 dV
 1400 km s-1,
so this yields
1400 km s-1,
so this yields  0
0
 0.2.
Either the mean density of the Universe is well below the critical
value
0.2.
Either the mean density of the Universe is well below the critical
value  = 1, or the Virgo cluster contains more than
its fair share of luminous galaxies, so that the excess mass density
= 1, or the Virgo cluster contains more than
its fair share of luminous galaxies, so that the excess mass density
 < 1.4. Some astronomers favor
the suggestion that the
distribution of luminous matter is lumpier than that of the total.
For example, perhaps galaxies can form and make their stars
only in the densest regions of the Universe. If the overdensity of
galaxies is a factor b greater than that of the matter, then
< 1.4. Some astronomers favor
the suggestion that the
distribution of luminous matter is lumpier than that of the total.
For example, perhaps galaxies can form and make their stars
only in the densest regions of the Universe. If the overdensity of
galaxies is a factor b greater than that of the matter, then
 = 1.4 / b. If
= 1.4 / b. If
 0 = 1, we require b
~ 4 to explain
the Virgocentric inflow.
This idea is known as biassed galaxy formation; we will see
in the next section why it has been popular.
0 = 1, we require b
~ 4 to explain
the Virgocentric inflow.
This idea is known as biassed galaxy formation; we will see
in the next section why it has been popular.
Further reading: On a graduate level, see T. Padmanabhan, 1993, Structure Formation in the Universe (Cambridge University Press, Cambridge, UK).