


Problem 2: Unequal errors
In the foregoing discussion, I assumed that all of the individual
yi
values had precisely the same typical expected error, quantified by
the so-called "standard error," which is defined as the Gaussian
 in
the probability distribution for
in
the probability distribution for
 . (Note that the standard error is
sometimes referred to as the "mean error" - standard error and mean
error mean the same thing. They are not the same thing as the
"probable error," which you will sometimes see mentioned in older
books and papers. The probable error is defined as the half-length of
a 50% confidence interval: when you give a numerical value for your
estimate of some physical quantity and quote a probable error, you are
saying that you think there is a 50% chance that the true value of
that quantity is within the stated error bars. The standard error =
the mean error is the half-length of a 68.3% confidence interval: when
you quote a standard or mean error, you are saying that you think
there's slightly over a two-thirds chance that the true value is
contained within your error bars. This latter is the current standard
astronomical convention.)
. (Note that the standard error is
sometimes referred to as the "mean error" - standard error and mean
error mean the same thing. They are not the same thing as the
"probable error," which you will sometimes see mentioned in older
books and papers. The probable error is defined as the half-length of
a 50% confidence interval: when you give a numerical value for your
estimate of some physical quantity and quote a probable error, you are
saying that you think there is a 50% chance that the true value of
that quantity is within the stated error bars. The standard error =
the mean error is the half-length of a 68.3% confidence interval: when
you quote a standard or mean error, you are saying that you think
there's slightly over a two-thirds chance that the true value is
contained within your error bars. This latter is the current standard
astronomical convention.)
In real life, it is commonly the case that the individual observations
have different known or estimated standard errors,
 i. This situation
is nearly as easy to deal with as the case of equal errors. We now
write the Gaussian function as
i. This situation
is nearly as easy to deal with as the case of equal errors. We now
write the Gaussian function as
so
where I have been very careful to keep the individual
You can see now that the specific value that you adopt for the
arbitrary constant s2 doesn't matter at all - since
the summations are
going to be set equal to zero anyway, whatever value of
s2 you use, it
can be pulled out of the summations and the equations are still true.
In matrix form we now have
or, in algebraic form,
In this case,
If you have used correct values for all the
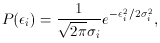
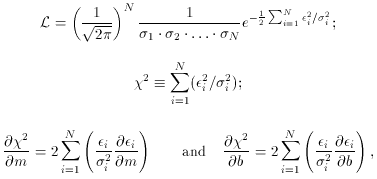
 's
throughout. Let us define the weight of an observation as
wi
's
throughout. Let us define the weight of an observation as
wi  = 2
s2 /
= 2
s2 /
 i2, where
s2 is just some arbitrary constant that you can pull out
of a hat; I have included it for generality and I have written it as
s2 to emphasize that it should be a positive constant. And
furthermore, . . . well, wait just a bit. Our conditions for a minimum
of
i2, where
s2 is just some arbitrary constant that you can pull out
of a hat; I have included it for generality and I have written it as
s2 to emphasize that it should be a positive constant. And
furthermore, . . . well, wait just a bit. Our conditions for a minimum
of  2 are:
2 are:
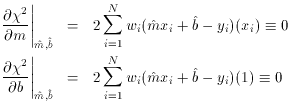
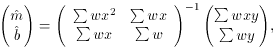
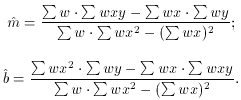
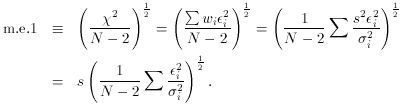
 i2, then
(1 / (N - 2)
i2, then
(1 / (N - 2) 
 i2 /
i2 /
 i2) is a
so-called "chi-squared" variable with an expected value of unity; it
will equal unity more and more precisely for larger and larger sample
sizes, N. Thus, if the
i2) is a
so-called "chi-squared" variable with an expected value of unity; it
will equal unity more and more precisely for larger and larger sample
sizes, N. Thus, if the
 i are correct, after
you have performed your
least-squares fit you should wind up with m.e.1
i are correct, after
you have performed your
least-squares fit you should wind up with m.e.1
 s. Recalling that s
is by definition the
s. Recalling that s
is by definition the  of an
observation of weight 1 (since w
of an
observation of weight 1 (since w
 s2 /
s2 /
 2), we
can now see why m.e.1 is called the "mean error of unit weight": it is
the mean error, or the correct value of
2), we
can now see why m.e.1 is called the "mean error of unit weight": it is
the mean error, or the correct value of
 , corresponding to a data
point with w = 1. If we are uncertain whether our assumed values of
the
, corresponding to a data
point with w = 1. If we are uncertain whether our assumed values of
the  i are correct,
we can use the derived m.e.1 as a guide. We start
off by setting s
i are correct,
we can use the derived m.e.1 as a guide. We start
off by setting s
 1. Then, if our values of
1. Then, if our values of
 are correct, the
derived m.e.1 should come out to have a value near 1.0. If, on the
other hand, the m.e.1 comes out with a value near 2.0, we would
suspect that we have underestimated our errors by a factor of two. On
the other hand, in many cases we do not know the true errors of all
our observations, but we have a good handle on their relative errors:
we may know that observation number 2 has a
are correct, the
derived m.e.1 should come out to have a value near 1.0. If, on the
other hand, the m.e.1 comes out with a value near 2.0, we would
suspect that we have underestimated our errors by a factor of two. On
the other hand, in many cases we do not know the true errors of all
our observations, but we have a good handle on their relative errors:
we may know that observation number 2 has a
 twice as large as
observation number 1, while not knowing what
twice as large as
observation number 1, while not knowing what
 1 and
1 and
 2 are, really. In
this case, we can arbitrarily assign observation 1 unit weight, and
observation 2 weight 1/4 (since weight
2 are, really. In
this case, we can arbitrarily assign observation 1 unit weight, and
observation 2 weight 1/4 (since weight

 -2. In this case m.e.1 will
not come out to unity, it will come out to an estimate of what
-2. In this case m.e.1 will
not come out to unity, it will come out to an estimate of what
 1
("the mean error of an observation of unit weight") actually should
have been.
1
("the mean error of an observation of unit weight") actually should
have been.