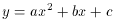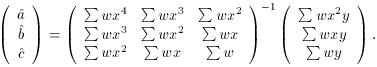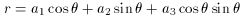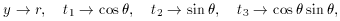Problems 3 and 4: More complex equations
The same methods may be used for more complicated equations. For instance, suppose our measured quantities yi depend upon three different known variables:
leads eventually to
(Prove it!) These matrices have a beautifully simple and symmetric
structure. I think that if you stare at them for a minute or two,
you'll be able to memorize their form and recall them whenever you
need them hereafter.
Notice that the known quantities t1,
t2, and t3 do not need to be
independent of each other. For instance, if t1
are easily seen to be
Or if
you can substitute
which gives
See? It's not called "linear" least squares because all it can do is
fit straight lines - it can fit all sorts of equations, provided they
are linear in the unknown parameters a, b, c, . . .
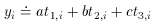
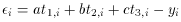
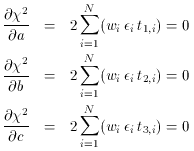
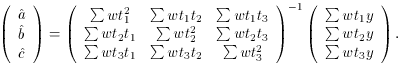
 x2,
t2
x2,
t2  x,
and t3
x,
and t3  1
then the coefficients of the best-fitting parabola
1
then the coefficients of the best-fitting parabola