


To repeat myself, the examples given above are all called "linear least squares." They are "least squares" because we derive our answers by minimizing the weighted sum of the squares of the residuals,
They are called "linear" because the equations which we must solve are
linear in the unknown quantities a, b, c, . . ., and not
because we are
fitting a "straight line" to the data. As I have already stated, these
methods may easily be generalized to larger problems.
Notation.
We have N sets of observations, each observation consisting of values
for n variables tj, i (j = 1, . . . ,
n) which are known perfectly, and
one dependent variable yi, which is subject to observational
error. Thus, we have N relations of the form
involving the n unknown quantities, or fitting parameters,
aj.
Problems 1 and 2: y
Problem 3: y
Problem 4: r
Step 1.
Write the equation in the form
Step 2.
Form the n x n matrix M and the n x 1 column vector
V:
Remember, wi = s2 /
Step 3.
Compute the n x 1 column vector containing the best estimates of
the fitting parameters A :
Step 4.
Compute the mean error of unit weight:
If you thought you knew your errors, but the m.e.1 comes out grossly
different from whatever value of s you adopted, then you've got a
problem. Most likely you've mis-estimated your errors, or maybe your
model is just wrong. (Remember that it's usually simplest to use
s
I guess that's pretty much it for the elegant theory behind linear
least squares. If you know enough computer programming to set up a
matrix, and if you have access to a math library with a matrix
inverter, YOU TOO can now do linear least squares to solve all sorts
of problems. (Of course, if you don't like to use computers, you can
always do it by hand!)
Now I'd like to show you a few things which will allow you to do least
squares just like the pros - a few tricks that you might not have
thought of.
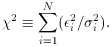
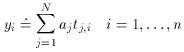
 mx + b
mx + b
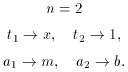
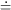 ax2 + bx
+ c
ax2 + bx
+ c
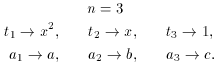
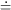 a1 cos
a1 cos
 + a2 cos
+ a2 cos
 + a3 cos
+ a3 cos
 sin
sin

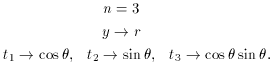
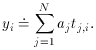
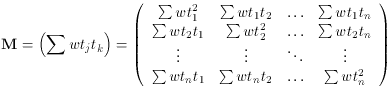
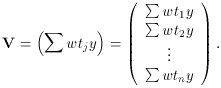
 i2. If
i2. If
 1 =
1 =
 2 = . . .
2 = . . .
 N =
N =
 , you might as well set
s =
, you might as well set
s =  and give
every observation weight 1.
and give
every observation weight 1.
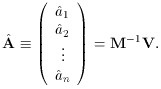
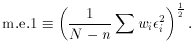
 1; then, you expect m.e.1
1; then, you expect m.e.1  1
to come out at the end.) If you didn't
know your errors to begin with, or rather if you only knew them to
within a scaling factor, m.e.1 is your best guess at that scaling factor.
1
to come out at the end.) If you didn't
know your errors to begin with, or rather if you only knew them to
within a scaling factor, m.e.1 is your best guess at that scaling factor.