


FIND
What you want a star-finder to do is find stars. Of course, it can't really do this - the most you can hope for is that it will identify most of the things in a digital image which look like stars. And the program really should consider how each object looks, because you can't just say that every group of pixels which is brighter than average is a star. In many CCD frames, especially those of star clusters or nearby galaxies, the diffuse sky brightness is different in different parts of the image. Any fixed brightness threshold which you would set might be just a little bit above the mean sky level in one part of the image, so that all sorts of noise spikes get picked up and identified as stars, while in some other part of the image the threshold is far above the local sky level, so that many faint stars are missed. What you really want to do is to search for little brightness peaks which stick up above the local sky brightness (whatever that happens to be) and which have approximately the correct diameter and profile for a star image in a frame of whatever sampling interval and seeing conditions you have. DAOPHOT does this in a crude way, by means of linear least squares.
The program asks the user to specify the full-width at half-maximum expected for stars in that frame, which is just the seeing diameter. (Precise knowledge of the actual seeing for the frame isn't really essential - it's usually adequate to divide the site's typical seeing, in arcseconds, by the scale of the telescope, in arcseconds per pixel, to get a good enough guess at the FWHM, in pixels. Although it is true that the seeing does vary from one frame to another in the course of a given night or observing run, it's unusual for it to vary by more than a factor of two or so. If necessary, for any given frame it's easy enough to estimate the FWHM by dumping or plotting the data in and around some bright star.) Once given a numerical value for the FWHM, DAOPHOT's FIND routine then assumes that the stellar profile is a circular Gaussian function with that full-width at half-maximum, and just goes through the entire picture fitting Gaussian profiles to a small region around every single pixel (excluding a narrow border around the frame): for each pixel (i0, j0) it performs the following fit
where
Notice that this is linear least squares so, in the notation of my first
lecture, FIND can
compute N,
(look familiar?) observed for the region around each
(i0, j0) tells FIND, if there were a star
centered at this (i0, j0), how
bright it would be above the local background.
There are a couple of little refinements that DAOPHOT's FIND adds to
this essentially
trivial concept. First, the user is allowed to specify two "bad-pixel"
thresholds: the
algorithm discards as "bad" any pixel whose brightness value is below
the first threshold (which the user should put, say,
7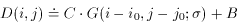

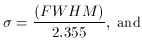

 x and,
x and,
 x2 ahead of time,
and only needs to
calculate
x2 ahead of time,
and only needs to
calculate  y and
y and
 xy afresh
for each point. Then
xy afresh
for each point. Then 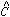 and
and
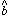 fall out directly. The value of
fall out directly. The value of
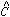 (i0,j0), where
(i0,j0), where
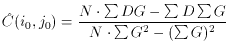
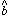 , which is
the estimate of the local sky brightness, is not needed so FIND doesn't
bother to compute it. In this way FIND builds up a new image,
, which is
the estimate of the local sky brightness, is not needed so FIND doesn't
bother to compute it. In this way FIND builds up a new image,
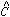 (i0,
j0), which has the local background,
and any simple gradients in the background, completely removed. (Since
the fitting region
around the point is symmetric, a gradient's positive contribution to the
sums on one side
is canceled by the equal negative contribution on the other.) It is then
simply a matter of picking out those pixels (a) where the value of
(i0,
j0), which has the local background,
and any simple gradients in the background, completely removed. (Since
the fitting region
around the point is symmetric, a gradient's positive contribution to the
sums on one side
is canceled by the equal negative contribution on the other.) It is then
simply a matter of picking out those pixels (a) where the value of
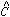 experiences a local
maximum (simply: any
pixel where the value of
experiences a local
maximum (simply: any
pixel where the value of 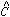 is
larger than in any other pixel within some radius), in order to
choose only the one pixel which is closest to the center of any given
star; and (b) where
is
larger than in any other pixel within some radius), in order to
choose only the one pixel which is closest to the center of any given
star; and (b) where 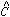 is larger than some user-specified multiple of
is larger than some user-specified multiple of
 (C), to eliminate random
noise peaks.
(C), to eliminate random
noise peaks.
 below the frame's mean sky level) or
above the second
(which should be the point at which the CCD response becomes nonlinear
due to incipient
saturation). To "discard" a pixel simply means that that pixel is
decremented from the
sums in the equation for
below the frame's mean sky level) or
above the second
(which should be the point at which the CCD response becomes nonlinear
due to incipient
saturation). To "discard" a pixel simply means that that pixel is
decremented from the
sums in the equation for 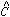 . Thus,
image flaws and bright cosmic-ray events are not carried
over into the derived image
. Thus,
image flaws and bright cosmic-ray events are not carried
over into the derived image
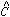 (i0,
j0), at a very small cost in extra computing
time. Second, after statistically significant local maxima in
(i0,
j0), at a very small cost in extra computing
time. Second, after statistically significant local maxima in
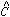 have been found, two
intensity moments
are computed from the corresponding pixels in the original image,
D. These represent
the sharpness (brightness in the central pixel of the peak as compared
to the surrounding
pixels) and roundness (second derivative of intensity with respect to
the y direction, as
compared to second derivative with respect to x). By rejecting oddballs
on the basis of
these criteria, FIND can go a long way toward eliminating cosmic rays,
charge-overflow
columns, and other image flaws which weren't extreme enough to be
eliminated by the
bad-data thresholds. Some background galaxies are also eliminated by
these limits, which
could be an advantage or a disadvantage depending on what you're
doing. Finally, the
FIND algorithm carries out precisely one iteration's worth of nonlinear
least squares on all
detections which have survived the various tests, to improve the
estimate of the centroid
position to better than the nearest pixel. These typically come out
precise to of order 0.2 pixels.
have been found, two
intensity moments
are computed from the corresponding pixels in the original image,
D. These represent
the sharpness (brightness in the central pixel of the peak as compared
to the surrounding
pixels) and roundness (second derivative of intensity with respect to
the y direction, as
compared to second derivative with respect to x). By rejecting oddballs
on the basis of
these criteria, FIND can go a long way toward eliminating cosmic rays,
charge-overflow
columns, and other image flaws which weren't extreme enough to be
eliminated by the
bad-data thresholds. Some background galaxies are also eliminated by
these limits, which
could be an advantage or a disadvantage depending on what you're
doing. Finally, the
FIND algorithm carries out precisely one iteration's worth of nonlinear
least squares on all
detections which have survived the various tests, to improve the
estimate of the centroid
position to better than the nearest pixel. These typically come out
precise to of order 0.2 pixels.