


B. Matching stars between frames
As I mentioned in the introduction, another chore you've got to be ready to handle is the cross-identification of the same stars observed in different CCD frames. On the face of it, you might think this task is pretty simple: when you find two stars at the same pixel location in the results obtained from two different images, they're the same star. Big deal. But when you stop and think about it, there are some subtleties that can turn horrendous on you. For instance, in the study that Bill Harris and I did of the globular cluster M92, there were seven deep frames for one field, each frame containing more than 3,000 stars. Since the exposures were not all taken the same night, they were not all centered exactly the same, but rather there were arbitrary translational shifts and even small rotational differences and scale changes among them. In another M92 field, we had 28 frames - 14 visual and 14 blue - containing roughly 1,000 stars and not only were they taken on different nights, they were obtained with two different telescopes. One of these telescopes was used at prime focus and the other at cassegrain, so there were large differences of scale and orientation, as well as a flip. I don't know about you, but I'm not going to sit down with a finding chart, an image display, and 28 printouts, and pull out the data relevant to each one of a thousand stars. This is a job for the computer! But computers are stupid!! You still have to tell the miserable machine how to relate the coordinate systems of all the frames to some common system. If you had to, you could go back to your image display, find the same three stars in each of the 28 images, and compute the necessary transformation constants for each frame from the observed pixel locations of those stars. But from any given observing run you might have two or three hundred images for half a dozen or more program fields, and dozens of standard-star fields. Is there any way to teach the computer how to recognize star fields all on its own, so you can read a good book while it does the boring stuff? Yes, there is.
Now I have to be very careful here. In 1985 I wrote a program to cross-identify matching triangles of stars appearing in two or more lists of star positions. In 1986 (May), Edward Groth of Princeton published an algorithm to do the same thing, and our two algorithms are similar in many ways. I know that Dr. Groth didn't get his ideas from me, because I had never given anyone a copy of my program, and I know I didn't get my ideas from him because I wrote my program before his paper came out (and I didn't see a preprint) - I have the backup tapes to prove it. Dr. Groth published and I didn't, so he clearly deserves full credit for the algorithm, or at least for those parts of it that are common to our two methods. I am not trying to steal his glory. Nevertheless, I am much more familiar with my method than with his, so that's the one I'm going to discuss now. Again, I don't want to imply that I think my method is any better (or worse) than his - I just prefer to talk about mine.
The basic idea is that any translation, rotation, scale change, or flip is not going to change the basic shape of a triangle, although of course it will change the size and orientation. The method, then, is to take the stars in each star list in groups of threes, and intercompare the shapes of the triangles that result. When a triangle in one star list is found to have the same shape as a triangle in the other list, provided the triangle is neither equilateral nor isosceles, then it's possible to cross-identify the stars uniquely: the star opposite the longest side of the triangle in one frame is - at least provisionally - equated to the star opposite the longest side of the similar triangle in the other frame, and so on. As always, there are a lot of details to straighten out before an simple concept like this can be converted into a working computer program. First of all, in any decent star list there may be thousands of stars. Since the number of distinct triangles in the list is n! / 3!(n - 3)! ~ n3 / 6 a field with 3000 stars, say, would contain 4.5 Gigatriangles. Each of these contains two independent shape parameters and, furthermore, each triangle must be associated with three pointers which connect the stored shape parameters back to the three particular stars which define the triangle, so that when a triangle in one frame has been matched with a similar triangle in the other, the corresponding stars can be matched as well. This is Many Data. This is a Prodigious Data-Handling Problem.
I tried to deal with it by starting as simply as possible. To begin with, each star list is sorted in order of increasing apparent magnitude; presuming that these lists have been generated by some aperture- or profile-fitting-photometry routine, good, relative apparent magnitudes will be available. Now we exploit the Universal Truth: in any star field and under any circumstances, bright stars will be rare and faint ones will be common. My program takes the three brightest stars from each list, and determines the shape of the triangle which they form. If the triangles from the two star lists have the "same" shape, then the stars at the corresponding vertices of the two triangles are provisionally cross-identified. Then the program takes the fourth brightest star from each list, determines the shape of the three new triangles that can be formed with this star and each possible pair from the other three, and intercompares their shapes. The program maintains a two dimensional table of cross-identifications: every time star i in the first frame is provisionally cross-identified with star j in the second frame, 1 is added to element (i,j) of the array. When star i in frame 1 is cross-identified with star j in frame 2 in enough different triangles (where "enough" depends upon how many triangles have been considered up to that point), star i is accepted as being the same object as star j. When enough different cross-identifications have been accepted, then a least-squares solution is performed to arrive at the actual, numerical transformation coefficients. Easy, isn't it?
There's another detail to consider: how are the shapes of the triangles encoded for storage and intercomparison? Well, when you allow for the fact that there may be arbitrary translations, rotations, scale changes, or flips of the positional coordinate system, each triangle contains - as I said - precisely two independent, invariant shape parameters. There are a number of ways that these parameters could be defined, but I chose to use the ratios of the sides: parameter 1 is the ratio of the length of the triangle's intermediate side to its longest side, b/a, and parameter 2 is the ratio of the shortest side to the longest side, c/a. By definition,
and
There is one other constraint that you might have to think about for a moment:
(If you have trouble figuring out why, try it in this form: b +
c
So now we've got it licked. In Fig. 5-12 I
show the output which my program generated
when I cross-identified a visual frame of an M92 field, which was taken
at the cassegrain
focus of the Kitt Peak #1-0.9m telescope, with a blue frame of roughly
the same field taken
at the prime focus of the 4m telescope: translation, rotation, scale
change, flip, different
filter. The rectangular arrays represent the table of provisional
cross-identifications which
is displayed each time a possible new match is found. You can see that
the program did
not find a single matching triangle until after it had considered the
eight brightest stars in
each frame. However, by the time it has considered the ten brightest
stars in each frame,
it has found five stars that it believes are common to the two
lists. Each of these five
tentative cross-identifications recurs in six different triangles,
making it pretty darn certain
that these identifications are correct. The entire process illustrated
in Fig. 5-12 required 10
seconds on a micro-VAX II, most of which was spent in simply sorting the
two star lists by
apparent magnitude. My experience is that if the intersection of the two
star lists is greater
than about 25% - that is, as long as there are at least 7 or 8 stars in
common among the
30 brightest stars in each frame - my program is sure to find the right
transformations.
If the overlap is less than 25%, it often turns out that the spurious
cross-identifications
among triangles that just happen to look alike can swamp the true
cross-identifications. (I
think that tweaking the criteria for deciding when two points in (b/a,
a/a)-space are "the
same" can help here.) So far I have restricted my program to considering
no more than the
thirty brightest stars from each frame; beyond that, the computations
take too long on a
micro-VAX II (i.e., more than 15 or 20 minutes, and the time grows as
n3). However, I
suppose I could relax this condition now that much faster computers are
becoming cheap.
So, now we've solved the first half of the problem: we've got at least
starting guesses
for the transformation constants relating one frame's coordinate system
to that of another.
We still have to cross-identify all the stars occurring in those two
frames - and perhaps in
many other frames as well. In general, this is a chore that can be done
by a good computer
program which doesn't require very much imagination. So, it really isn't
interesting enough
to talk about it now. There are only a couple of comments I'd like to make.
First of all, different transformation rules may be useful under
different circumstances.
For instance, if you're intercomparing frames that were taken one right
after another with
the same telescope, it would probably be enough to solve for simple
positional offsets:
Under most circumstances, i.e., with frames taken with the same
telescope on different
nights or during different observing runs, or even frames taken with
different telescopes,
you can often get away with a four-parameter transformation:
(I showed you how to solve this one in the first lecture). In some
cases, though, there may be
a tilt of the detector with respect to the optical axis, or unequal
scales in the two coordinates for some other reason, and you'll have to
go to a full, six-parameter transformation:
Frame 2:
star 1 2 3 4 5 6 7 8
+----------------
Frame 1: 1 | 0 0 0 0 1 0 0 0
2 | 0 0 0 0 0 0 1 0
3 | 0 0 0 0 0 0 0 1
4 | 0 0 0 0 0 0 0 0
5 | 0 0 0 0 0 0 0 0
6 | 0 0 0 0 0 0 0 0
7 | 0 0 0 0 0 0 0 0
8 | 0 0 0 0 0 0 0 0
(Star 1, Frame 1) matches (Star 5, Frame 2)?
(Star 2, Frame 1) matches (Star 7, Frame 2)?
(Star 3, Frame 1) matches (Star 8, Frame 2)?
Estimated transformation:
x(1) = 336.9172 + -1.2157 x(2) + -0.0267 y(2)
y(1) = -111.9601 + -0.0253 x(2) + 1.2242 y(2)
Another level? Y
Frame 2:
star 1 2 3 4 5 6 7 8 9
+------------------
Frame 1:1 | 0 0 0 0 3 0 0 0 0
2 | 0 0 0 0 0 0 3 0 0
3 | 0 0 0 0 0 0 0 3 0
4 | 0 0 0 0 0 0 0 0 0
5 | 0 0 0 0 0 0 0 0 3
6 | 0 0 0 0 0 0 0 0 0
7 | 0 0 0 0 0 0 0 0 0
8 | 0 0 0 0 0 0 0 0 0
9 | 0 0 0 0 0 0 0 0 0
(Star 1, Frame 1) matches (Star 5, Frame 2)?
(Star 2, Frame 1) matches (Star 7, Frame 2)?
(Star 3, Frame 1) matches (Star 8, Frame 2)?
(Star 5, Frame 1) matches (Star 9, Frame 2)?
Estimated transformation:
x(1) = 337.7639 + -1.2223 x(2) + -0.0276 y(2)
y(1) = -111.5454 + -0.0286 x(2) + 1.2238 y(2)
Another level? Y
Frame 2:
star 1 2 3 4 5 6 7 8 9 10
+---------------------
Frame 1: 1 | 0 0 0 0 6 0 0 0 0 0
2 | 0 0 0 0 0 0 6 0 0 0
3 | 0 0 0 0 0 0 0 6 0 0
4 | 0 0 0 0 0 0 0 0 0 6
5 | 0 0 0 0 0 0 0 0 6 0
6 | 0 0 0 0 0 0 0 0 0 0
7 | 0 0 0 0 0 0 0 0 0 0
8 | 0 0 0 0 0 0 0 0 0 0
9 | 0 0 0 0 0 0 0 0 0 0
10 | 0 0 0 0 0 0 0 0 0 0
(Star 1, Frame 1) matches (Star 5, Frame 2)?
(Star 2, Frame 1) matches (Star 7, Frame 2)?
(Star 3, Frame 1) matches (Star 8, Frame 2)?
(Star 4, Frame 1) matches (Star 10, Frame 2)?
(Star 5, Frame 1) matches (Star 9, Frame 2)?
Estimated transformation:
x(1) = 337.6446 + -1.2216 x(2) + -0.0274 y(2)
y(1) = -111.8034 + -0.0271 x(2) + 1.2242 y(2)
Another level? Y
Frame 2:
star 1 2 3 4 5 6 7 8 9 10 11 12
+-----------------------------------------
Frame 1:1 | 0 0 0 0 10 0 0 0 0 0 0 0
2 | 0 0 0 0 0 0 10 0 0 0 0 0
3 | 0 0 0 0 0 0 0 10 0 0 0 0
4 | 0 0 0 0 0 0 0 0 0 10 0 0
5 | 0 0 0 0 0 0 0 0 10 0 0 0
6 | 0 0 0 0 0 0 0 0 0 0 0 10
7 | 0 0 0 0 0 0 0 0 0 0 0 0
8 | 0 0 0 0 0 0 0 0 0 0 0 0
9 | 0 0 0 0 0 0 0 0 0 0 0 0
10 | 0 0 0 0 0 0 0 0 0 0 0 0
11 | 0 0 0 0 0 0 0 0 0 0 0 0
12 | 0 0 0 0 0 0 0 0 0 0 0 0
(Star 1, Frame 1) matches (Star 5, Frame 2)?
(Star 2, Frame 1) matches (Star 7, Frame 2)?
(Star 3, Frame 1) matches (Star 8, Frame 2)?
(Star 4, Frame 1) matches (Star 10, Frame 2)?
(Star 5, Frame 1) matches (Star 9, Frame 2)?
(Star 6, Frame 1) matches (Star 12, Frame 2)?
Estimated transformation:
x(1) = 337.6414 + -1.2216 x(2) + -.0274 y(2)
y(1) = -111.9123 + -0.0266 x(2) + 1.2244 y(2)
Another level? Y
Frame 2:
star 1 2 3 4 5 6 7 8 9 10 11 12 13 14
+-----------------------------------------------
Frame 1:1 | 0 0 0 0 15 0 0 0 0 0 0 0 0 0
2 | 0 0 0 0 0 0 15 0 0 0 0 0 0 0
3 | 0 0 0 0 0 0 0 15 0 0 0 0 0 0
4 | 0 0 0 0 0 0 0 0 0 15 0 0 0 0
5 | 0 0 0 0 0 0 0 0 15 0 0 0 0 0
6 | 0 0 0 0 0 0 0 0 0 0 0 15 0 0
7 | 0 0 0 0 0 0 0 0 0 0 0 0 0 15
8 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
9 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
11 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
13 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
14 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(Star 1, Frame 1) matches (Star 5, Frame 2)?
(Star 2, Frame 1) matches (Star 7, Frame 2)?
(Star 3, Frame 1) matches (Star 8, Frame 2)?
(Star 4, Frame 1) matches (Star 10, Frame 2)?
(Star 5, Frame 1) matches (Star 9, Frame 2)?
(Star 6, Frame 1) matches (Star 12, Frame 2)?
(Star 7, Frame 1) matches (Star 14, Frame 2)?
Estimated transformation:
x(1) = 337.6680 + -1.2217 x(2) + -0.0274 y(2)
y(l) = -111.8624 + -0.0268 x(2) + 1.2244 y(2)
Another level? N
$
If you're trying to do milliarcsecond astrometry, you'll certainly want
to include terms that
depend upon the color of the star, and you might conceivably want to
include quadratic
positional terms, but in cross-matching lists for purposes of committing
photometry, in my
experience linear positional transformations have always been fine.
The only thing that's at all subtle about cross-matching stars is
deciding when a star
is a single and when it's a double. In order to acquaint you with the
problem, I must
give you a quick run-down of how my star-matching program works. You
feed it a list
of the names of N input files, each of which contains the positions and
magnitudes of
stars from a CCD frame. The program starts off by considering the first
input list as a
"master" list. Taking each star in turn from the second input list, it
applies the provisional
transformations derived by the triangle-matching program to determine
the star's position
in the coordinate system of the master list. It then goes through the
master list, looking for
that star which lies closest to the transformed position of the star
from list 2. If it does find
a star in the master list which is within some critical distance of the
transformed position
(initially several pixels, since the provisional transformations may not
be very good, and
since the positions in both frames will be subject to random errors;
over the course of several
iterations, as the transformations and the "master" positions improve
through iteration, the
critical distance will be reduced to maybe one or one and a half
pixels), the star from list 2
is provisionally identified with that star in the master list. If that
star in the master list had
already been provisionally identified with some other star from list 2,
whichever star has
a transformed position closer to the "master" position will remain
provisionally identified
with it; the other gets "bumped" and must go off looking for some other
star in the master
list that it can be identified with. Any star in list 2 which has no
star in the current master
list within the critical radius, is added to the master list as a
putative new detection.
Once all possible cross-identifications between list 2 and the master
list have been
made, they are used for a new least-squares determination of the
transformation equations.
The original transformation coefficients derived by the
triangle-matching program may not
very precise, after all, because they have been derived from - typically
- only five or six or
seven of the brightest stars in the field. Furthermore, there is no
particular guarantee that
these stars will be well-distributed over the field, especially if the
region of overlap between
the two frames is comparatively small. The new transformations should be
much better
than the old, because they can be based upon the hundreds or thousands
of stars common
to the two frames. Furthermore, as the other frames of the field are
included and the whole
process is iterated (see below) the area of overlap between any one
frame and the current
master list will increase, yielding additional leverage on the
transformation equations.
The same process is carried out with frames 3, ... , N.
Now, after all possible cross-identifications among all the stars in all
the frames have
been made, the resulting master list may be culled. For instance, if you
have seven CCD
frames, you might say that you are only interested in a star which
appears in at least three
of those seven frames; any star which appears in only one or two frames
you might regard
as too likely to be a spurious detection. As an alternative or
additional constraint, you
might say that you are only interested in a star whose mean magnitude,
after averaging
however many magnitudes are available for it from the various frames, is
known to better
than, say, 0.2 mag. (For instance, if you want to define a
color-magnitude diagram with
the tightest possible sequences, but you aren't interested in the
luminosity function so you
don't care about completeness, you might only want to retain the best
data.) The choices
you make will depend upon the circumstances, but in any case at this
point you have the
opportunity to prune the new master list. The new list will probably
include some stars
which did not appear in frame 1, but did appear in some subset of frames
2, ..., 7. The
estimated (x, y) position of each star in this augmented master list is
improved at this
point, by averaging together all the (transformed) positions available
for it from all the
frames in which it is found. Now the process is repeated, comparing
frames 1, ..., N to the
new master list. Because the previous run-through has improved both the
accuracy of the
positional transformation equations and the precision of the "master"
positions, it is now
possible to reduce the size of the "critical distance" for regarding
detections from different
frames as the same star; this reduces the probability of spuriously
equating unrelated objects
(which happens more often than you'd like to think, in a crowded field
with image flaws,
cosmic ray events, and the like). The whole process is repeated a couple
more times, with
the transformation equations and the master positions getting better and
better as the
critical distance is reduced further and further and a purer and purer
list of legitimate
cross-identifications is produced.
Here comes the subtle part. Sometimes an object which the
profile-fitting software
regards as a single star in one frame is reduced as though it were a
double star in another
frame. This can't be helped; sometimes a noise spike just seems to put a
second peak on
the flank of a star image. This may not seem like a big problem, but if
you are obsessed
with seemingly trivial details (the way I am), you worry about it. What
happens when you
have a single object appearing at some (x, y) position in the master
list, where one of the
individual CCD frames has a "double" star very near that same position?
Since we are
treating all detections as equal until proven otherwise, what will
happen is one component
of the "double" star will be provisionally identified with the entry in
the master list, while
the other component of the "double" will be added to the master list as
an apparent "new
detection." What happens then? As the subsequent frames are considered
they find that
the master list contains two entries near the same position - and they
can be provisionally
identified with whichever one they happen to lie closer to (see
Fig. 5-13a). Given the random
errors in any given positional determination, the stars in some of these
subsequent frames
will be matched up with the original entry in the master list, while
some will be matched
with the new one. At the end of the iteration, when we come to clean the
master list of
false entries, we are likely to find that each of these entries appears
to have been found in
at least three of the seven frames, so both are kept and the star -
single in six frames,
double in only one - goes into the final master catalog as a close double.
What do you do? Well, the simplest thing is to retain only those
detections which are
found in more than half of the input frames, but sometimes you just
don't want to do this.
Suppose you are trying to derive a master list for a large array of
images that have only
partial overlap, because you were trying to cover some cluster that was
much bigger than an
individual CCD frame? In this case there may be no portion of the
cluster which appears
in more than half of the frames. Or suppose you wanted to derive a
luminosity function for
some field where the frames were almost perfectly coincident, but had
significantly different
magnitude limits? In this case you'd find yourself throwing away
legitimate detections
from the deep frames, because they didn't also appear in the shallow
frames. Besides, as
illustrated in Fig. 5-13, it's possible to
imagine that each of the "objects" might seem to
have been found in four of the seven frames.
My solution was simply this. Require that each detection in each of the
individual
frames must first look for an object at the corresponding position in
the initial master
list for that iteration; if there is an otherwise unmatched object in
the initial master list
within the critical distance, the provisional match must be made with it
even if some other
"new detection" which has been added during this iteration seems to be
closer. Thus, as
illustrated in Fig. 5-13b, each detection
near that location in frames 4, ... ,7 must associate
itself with the original star from frame 1, even if the "new" star which
was found only in
frame 3 seems closer. At the end of the first iteration, the "new" star
from frame 3 has still
been found in only the one frame, so it disappears in the culling
process, and the master
list goes into iteration 2 with only a single object at that location. This solves most of the
problem.
The only thing: Suppose that it was in frame 1 that the object appeared
to be double
(Fig. 5-13c). I haven't yet figured out the
answer to this one. Got any good ideas? It
seems to me that it should be possible to modify the culling process so
that a star may be
"double" in the output master list only if is "double" in at least three
(or however many) of
the seven input lists. But should a double with position angle 90° in
frame 1 be considered
to have been confirmed by a double with position angle 30° in frame 3
and another double
with position angle 160° in frame 6? Details, details, ...
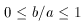
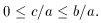
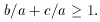
 a.)
Thus, given some triangle
defined by three arbitrary points in some (x, y)-space, that triangle
can be represented by
a point in two-dimensional (b/a, c/a)-space. Because of the obvious
definitions just given,
not all parts of (b/a, c/a)-space can be occupied
(Fig. 5-11), but the
same three stars - no
matter how you shift, rotate, expand, contract, or flip the coordinate
system - will always
be projected to the same point in (b/a, c/a) space.
a.)
Thus, given some triangle
defined by three arbitrary points in some (x, y)-space, that triangle
can be represented by
a point in two-dimensional (b/a, c/a)-space. Because of the obvious
definitions just given,
not all parts of (b/a, c/a)-space can be occupied
(Fig. 5-11), but the
same three stars - no
matter how you shift, rotate, expand, contract, or flip the coordinate
system - will always
be projected to the same point in (b/a, c/a) space.
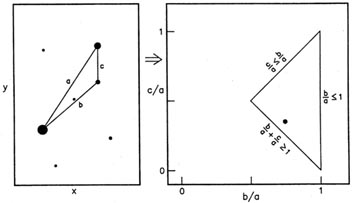
Figure 5-11.
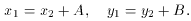
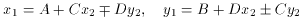
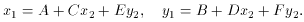
$ RUN MATCH
Input file: KP36:A58.ALS
Input file: KP4M:D63.ALS
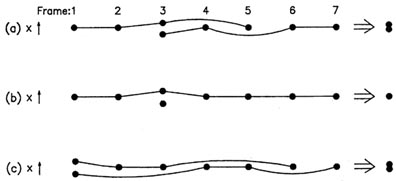
Figure 5-13.