8. DISCUSSION AND CONCLUSIONS

The complicating effects of galactic chemical evolution for age determinations have been largely ignored in our discussions. The basic equations on which such studies are based are those shown in Section 3. There exists a very substantial literature concerning chemical evolution effects on age dating, including considerations of varied prescriptions for the star formation history, and of the consequences of infall and outflow of gas from the star forming regions. This literature has been reviewed most recently by Cowan, Thielemann, & Truran (1991a, b), and their Table 3 summarizes the galactic ages obtained from both r-process and other chronometers, by a variety of authors. These, again, are generally quite model-dependent age determinations.

Meyer & Schramm (1986), extending the early work by Schramm & Wasserburg (1970) sought to provide a `model independent' age determination. They noted that the general expression we have derived for N_i(T) is dependent upon the effective nucleosynthesis rat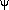e e, such that any age determination requires information about galactic chemical evolution. In an attempt to minimize such dependence, they choose to expand the equation for N_i(T) in moments of the production function about the mean age t_m given by (Tinsley 1980)

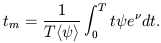
In the limit of long-lived chronometers (T << 1), they derive a simple expression for the age that is approximately independent of galactic evolution effects. Proceeding in this manner, they obtained a `nearly model-independent' range for T_Galaxy of 8.7 T_Galaxy 28.1 Gyr. In fact, this range is quite compatible with the different age determinations by other authors. That is, model dependent age estimates, with parameters that otherwise fit general galactic evolution abundance trends, yield ages in the range ~ 10-20 Gyr.

In general, the observational and theoretical considerations briefly reviewed in this paper allow the following conclusions:

• The important nuclear chronometers are r-process products.

• The identification of the r-process site with massive stars, supported by the observations of r-process abundance patterns in halo stars, implies that the critical chronometers for dating the Galaxy were formed early in galactic history and were produced at rates proportional to the SFR.

• Lower bounds on the age of the elements based upon the assumption of a single nucleosynthesis event can be obtained from both the ²³⁵U / ²³⁸U and ²³²Th / ²³⁸U chronometric pairs, yielding (T + _SS) > 6.3 ± 0.25 Gyr for ²³⁵U / ²³⁸U and (T + _SS) > 7.9 ± 1.20 Gyr for ²³²Th / ²³⁸U.

• The very presence of shorter lived r-process chronometers such as ¹²⁹I, ¹⁸²Hf, and ²⁴⁴Pu in primitive solar system matter demands some level of recent r-process nucleosynthesis. This will necessarily yield longer age estimates for the epoch of galactic nucleosynthesis than are predicted for a single event model. For such a constant nucleosynthesis history, we obtain from consideration of the ²³²Th-²³⁸U chronometer pair an age estimate for the Galaxy of (T + _SS) = 12.8 ± 3 Gyr.

• The thorium abundance obtained for the halo star CS 22892-052 by Sneden et al. (1996), with the assumption that there has been no evolution of the (Th / Eu)_ISM ratio over the course of galactic evolution (in other words, that the primordial ratio Th / Eu for CS 22892-052 was identical to that of the Sun), yields an age for the star of approximately 15.2 Gyr, with an allowed range of ages of approximately 10-20 Gyr.

• The poverty of nucleocosmochronology remains the fact that, given the present levels of uncertainty associated with the nuclear physics and astrophysics of the r-process and with galactic evolution, a tighter constraint on the age of the Galaxy, and thus a more realistic bound on the age of the Universe, is not possible.