


Most of our present understanding of the Universe is concisely
and beautifully summarized in the hot big-bang cosmological model
(see e.g.,
Weinberg 1972;
Peebles, 1993).
This mathematical description is based upon the
isotropic and homogeneous Friedmann-Lemaitre-Robertson-Walker
solution of Einstein's general relativity. The evolution of
the Universe is embodied in the cosmic scale factor R(t), which
describes the scaling up of all physical distances in the Universe
(separation of galaxies and wavelengths of photons).
The conformal stretching of the wavelengths of photons
accounts for the redshift of light from distant galaxies:
the wavelength of the radiation we see today is larger by
the factor R (now) / R (then). Astronomers
denote this factor by 1 + z, which means that an object
at ``redshift z'' emitted the light seen today when the
Universe was a factor 1 + z smaller. Normalizing the
scale factor to unity today, Remission = 1 / (1 + z).
It is interesting
to note that the assumption of isotropy and homogeneity was introduced
by Einstein and others to simplify the mathematics; as it turns out,
it is a remarkably accurate description at early times and today
averaged over sufficiently large distances (greater than 100 Mpc or so).
The evolution of the scale factor is governed by the Friedmann equation
for the expansion rate:
where
The energy density of a given component evolves according to
where pi is the pressure (e.g., pi
<<
It is convenient to scale
energy densities to the critical density,
Note that the critical-density Universe (
There are at least two components to the energy density:
the photons in the 2.728 K cosmic microwave background radiation
(number density n
There is strong evidence for the existence of matter beyond
the baryons, as dynamical measurements of the matter density
indicate that it is at least 20% of the critical density
(
Finally, although it is now known that the mass density of the Universe
in the form of dark matter exceeds 0.2 of the closure density, there are
even more exotic possibilities for additional components to the mass-energy
density, the simplest of which is Einstein's
cosmological constant. Seeking static solutions, Einstein introduced
his infamous cosmological constant; after the discovery of the
expansion by Hubble he discarded it. In the quantum world it
is no longer optional: the cosmological constant represents
the energy density of the quantum vacuum
(Weinberg 1989;
Carroll et al. 1992).
Lorentz invariance implies that the pressure associated
with vacuum energy is pVAC = -
All attempts to calculate the
cosmological constant have been unsuccessful to say the very
least: due to the zero-point energies the vacuum energy formally
diverges (``the ultraviolet catastrophe''). Imposing a short wavelength
cutoff corresponding to the weak scale (~ 10-17 cm)
is of little help:
Because the different contributions to the energy density
scale differently with the cosmic scale factor, the expansion
of the Universe goes through qualitatively different phases.
While today radiation and relativistic particles are not
significant, at early times they dominated the energy, since
their energy density depends most strongly on the scale factor
(R-4 vs. R-3 for matter). Only at
late times does
the curvature term (
The presence of a cosmological constant, which is independent
of scale factor, changes this a little. A flat or negatively
curved Universe ultimately enters an exponential expansion
phase driven by the cosmological constant. This also occurs
for a positively curved Universe, provided the cosmological
constant is large enough,
If it is smaller than this, recollapse
occurs. Einstein's static Universe obtains for
The evolution of the Universe according to the standard hot big-bang
model is summarized as follows:
Radiation-dominated phase. At times earlier than
about 10,000 yrs, when the temperature exceeded kBT
Matter-dominated phase. When the
temperature reached
around kBT ~ 3 eV, at a time of around 10,000 years, the
energy density in matter began to exceed that in radiation. At
this time the Universe was about 10-4 of its present size
and the cosmic-scale factor began to grow as R(t)
Curvature-dominated or cosmological constant
dominated phase. If the Universe is negatively curved and there
is no cosmological constant, then when the size of Universe is
Finally, a comment on the expansion rate and the size of
the ``observable Universe.''
The inverse of the expansion rate has units of time. The Hubble time,
H-1,
corresponds to the time it takes for the scale factor to roughly
double. For a matter-, radiation-, or curvature-dominated
Universe, the age of the Universe (time back to zero scale factor)
is: 2/3 H-1, 1/2 H-1, and
H-1 respectively.
The Hubble time also sets the size of the observable (or causally
connected) Universe: the distance to the ``horizon,''
which is equal to the distance that light could have traveled
since time zero, is 2t = H-1 for a radiation-dominated
Universe and 3t = 2H-1 for a matter-dominated
Universe. Paradoxically, although the size of the Universe goes to zero
as one goes back to time zero, the expansion rate is larger,
and so points separated by distance t are moving apart faster
than light can catch up with them.
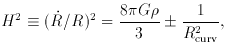
 =
=  i
i  i is the
total energy density from all
components of mass-energy, and Rcurv is
the spatial curvature radius, which grows as the scale factor,
Rcurv
i is the
total energy density from all
components of mass-energy, and Rcurv is
the spatial curvature radius, which grows as the scale factor,
Rcurv  R(t). [Hereafter we shall set c = 1.] As indicated
by the ± sign in Eq. (3)
there are actually three FLRW models; they differ in their spatial curvature:
The plus sign applies to the negatively curved model, and the minus
sign to the positively curved model. For the spatially flat
model the curvature term is absent.
R(t). [Hereafter we shall set c = 1.] As indicated
by the ± sign in Eq. (3)
there are actually three FLRW models; they differ in their spatial curvature:
The plus sign applies to the negatively curved model, and the minus
sign to the positively curved model. For the spatially flat
model the curvature term is absent.
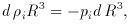
 i for nonrelativistic
matter or pi =
i for nonrelativistic
matter or pi =  i / 3 for ultra-relativistic particles
and radiation). The energy density of matter decreases as
R-3, due to volume dilution. The energy density of
radiation decreases more rapidly, as R-4, the additional
factor arising because the energy of a relativistic particle
``redshifts'' with the expansion, E
i / 3 for ultra-relativistic particles
and radiation). The energy density of matter decreases as
R-3, due to volume dilution. The energy density of
radiation decreases more rapidly, as R-4, the additional
factor arising because the energy of a relativistic particle
``redshifts'' with the expansion, E  1 / R(t). (This
of course is equivalent to the wavelength of a photon growing
as the scale factor.) This redshifting of the energy
density of radiation by R-4 also implies that
for black body radiation, the temperature decreases
as T
1 / R(t). (This
of course is equivalent to the wavelength of a photon growing
as the scale factor.) This redshifting of the energy
density of radiation by R-4 also implies that
for black body radiation, the temperature decreases
as T  R-1.
R-1.
 crit
crit  3H02 / 8
3H02 / 8 G = 1.88h2 x
10-29 g cm-3
G = 1.88h2 x
10-29 g cm-3  8.4 x
10-30 g cm-3 or approximately 5 protons per cubic meter,
8.4 x
10-30 g cm-3 or approximately 5 protons per cubic meter,
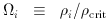
 0 = 1) is flat;
the subcritical-density Universe (
0 = 1) is flat;
the subcritical-density Universe ( 0 < 1) is negatively
curved; and the supercritical-density Universe (
0 < 1) is negatively
curved; and the supercritical-density Universe ( 0 > 1) is positively curved.
0 > 1) is positively curved.
 = 412 cm-3); and
ordinary matter in the formation of neutrons, protons and
associated electrons (referred to collectively as baryons).
The theory of big-bang nucleosynthesis and the
measured primordial abundance of deuterium imply that
the mass density contributed by baryons is
= 412 cm-3); and
ordinary matter in the formation of neutrons, protons and
associated electrons (referred to collectively as baryons).
The theory of big-bang nucleosynthesis and the
measured primordial abundance of deuterium imply that
the mass density contributed by baryons is  B =
(0.02 ± 0.002)h-2
B =
(0.02 ± 0.002)h-2  0.05. In addition, the
weak interactions of neutrinos with electrons, positrons
and nucleons should have brought all three species of
neutrinos into thermal equilibrium when the Universe
was less than a second old, so that today there should
be three cosmic seas of relic neutrinos of comparable
abundance to the microwave photons, n
0.05. In addition, the
weak interactions of neutrinos with electrons, positrons
and nucleons should have brought all three species of
neutrinos into thermal equilibrium when the Universe
was less than a second old, so that today there should
be three cosmic seas of relic neutrinos of comparable
abundance to the microwave photons, n = (3 / 11)
n
= (3 / 11)
n
 113
cm-3 (per species). (BBN provides a
nice check of this, because the yields depend sensitively upon the
abundance of neutrinos.) Together, photons and neutrinos
(assuming all three species are massless, or very light, <<
10-3 eV) contribute a very small energy density
113
cm-3 (per species). (BBN provides a
nice check of this, because the yields depend sensitively upon the
abundance of neutrinos.) Together, photons and neutrinos
(assuming all three species are massless, or very light, <<
10-3 eV) contribute a very small energy density


 =
4.17h-2 x 10-5
=
4.17h-2 x 10-5  10-4.
10-4.
 M > 0.2),
which is far more than ordinary matter
can account for. The leading explanation for the additional
matter is long-lived or stable elementary particles left over
from the earliest moments (see Section 5).
M > 0.2),
which is far more than ordinary matter
can account for. The leading explanation for the additional
matter is long-lived or stable elementary particles left over
from the earliest moments (see Section 5).
 VAC, and this
ensures that
VAC, and this
ensures that  VAC remains constant as the Universe
expands. Einstein's cosmological constant appears as an additional term
VAC remains constant as the Universe
expands. Einstein's cosmological constant appears as an additional term
 / 3
on the right hand side of the Friedmann equation [Equ. 3]; it is equivalent
to a vacuum energy
/ 3
on the right hand side of the Friedmann equation [Equ. 3]; it is equivalent
to a vacuum energy  VAC =
VAC =  / 8
/ 8 G.
G.
 VAC ~ 1055!
The mystery of the cosmological constant is a fundamental one which
is being attacked from both ends: Cosmologists are trying to
measure it, and particle physicists are trying to understand
why it is so small.
VAC ~ 1055!
The mystery of the cosmological constant is a fundamental one which
is being attacked from both ends: Cosmologists are trying to
measure it, and particle physicists are trying to understand
why it is so small.
 R-2) become important; for
a negatively curved Universe it becomes dominant. For a
positively curved Universe, the expansion halts when it cancels
the matter density term and a contraction phase begins.
R-2) become important; for
a negatively curved Universe it becomes dominant. For a
positively curved Universe, the expansion halts when it cancels
the matter density term and a contraction phase begins.
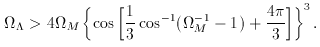
 M =
2
M =
2 VAC and
Rcurv = 1/sqrt(8
VAC and
Rcurv = 1/sqrt(8 G
G  VAC).
VAC).
 3 eV,
the energy density in radiation and relativistic particles exceeded
that in matter. The scale factor grew as t1/2 and the
temperature decreased as kBT ~ 1 MeV
(t/sec)-1/2.
At the earliest times, the energy in the Universe consists of
radiation and seas of relativistic particle - antiparticle pairs. (When
kBT >> mc2 pair creation makes
particle - antiparticle
pairs as abundant as photons.) The standard model of particle
physics, the
3 eV,
the energy density in radiation and relativistic particles exceeded
that in matter. The scale factor grew as t1/2 and the
temperature decreased as kBT ~ 1 MeV
(t/sec)-1/2.
At the earliest times, the energy in the Universe consists of
radiation and seas of relativistic particle - antiparticle pairs. (When
kBT >> mc2 pair creation makes
particle - antiparticle
pairs as abundant as photons.) The standard model of particle
physics, the 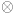 SU(2)
SU(2) 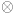 U(1)
U(1) t2/3.
Once the Universe became matter-dominated, primeval inhomogeneities in
the density of matter (mostly dark matter), shown to be of size
around
t2/3.
Once the Universe became matter-dominated, primeval inhomogeneities in
the density of matter (mostly dark matter), shown to be of size
around 
 /
/ ~ 10-5
by COBE and other anisotropy experiments,
began to grow under the attractive influence of gravity
(
~ 10-5
by COBE and other anisotropy experiments,
began to grow under the attractive influence of gravity
(
 /
/ 
 R). After 13 billion or so years
of gravitational amplification, these tiny primeval density
inhomogeneities developed into all the structure that we see
in the Universe today, galaxies, clusters of the galaxies,
superclusters, great walls, and voids. Shortly after matter
domination begins, at a redshift 1 + z
R). After 13 billion or so years
of gravitational amplification, these tiny primeval density
inhomogeneities developed into all the structure that we see
in the Universe today, galaxies, clusters of the galaxies,
superclusters, great walls, and voids. Shortly after matter
domination begins, at a redshift 1 + z  1100, photons
in the Universe undergo their last-scattering off free electrons;
last-scattering is precipitated by the recombination of electrons
and ions (mainly free protons), which occurs at a
temperature of kBT ~ 0.3 eV because neutral atoms are
energetically favored. Before last-scattering, matter and radiation
are tightly coupled;
after last-scattering, matter and radiation are essentially decoupled.
1100, photons
in the Universe undergo their last-scattering off free electrons;
last-scattering is precipitated by the recombination of electrons
and ions (mainly free protons), which occurs at a
temperature of kBT ~ 0.3 eV because neutral atoms are
energetically favored. Before last-scattering, matter and radiation
are tightly coupled;
after last-scattering, matter and radiation are essentially decoupled.
 M / (1 -
M / (1 -  M) ~
M) ~  M times its
present size the epoch
of curvature domination begins (i.e., Rcurv-2
becomes the dominant term on the right hand side
of Friedmann equation). From this
point forward the expansion no longer slows and R(t)
M times its
present size the epoch
of curvature domination begins (i.e., Rcurv-2
becomes the dominant term on the right hand side
of Friedmann equation). From this
point forward the expansion no longer slows and R(t)  t
(free expansion). In the case of a cosmological constant
and a flat Universe, the cosmological constant becomes
dominant when the size of the Universe is [
t
(free expansion). In the case of a cosmological constant
and a flat Universe, the cosmological constant becomes
dominant when the size of the Universe is [ M / (1 -
M / (1 -  M)]1/3.
Thereafter, the scale factor grows exponentially.
In either case, further growth of density inhomogeneities that
are still linear (
M)]1/3.
Thereafter, the scale factor grows exponentially.
In either case, further growth of density inhomogeneities that
are still linear (
 /
/  < 1) ceases. The
structure that exists in the Universe is frozen in.
< 1) ceases. The
structure that exists in the Universe is frozen in.