


5.1 Dark Matter and Dark Energy
Our knowledge of the mass and energy content of the Universe
is still poor, but is improving rapidly (see
Sadoulet 1999).
We can confidently say that most of the matter in the Universe is
of unknown form and dark (see e.g.,
Dekel et al. 1997;
Bahcall et al. 1993):
Stars (and closely related material)
contribute a tiny fraction of the critical density,  lum
= (0.003 ± 0.001) h-1
lum
= (0.003 ± 0.001) h-1  0.004, while the amount of matter
known to
be present from its gravitational effects contributes around
ten times this amount,
0.004, while the amount of matter
known to
be present from its gravitational effects contributes around
ten times this amount,  M = 0.35 ± 0.07 (this error
flag is ours; it is meant to indicate 95% certainty that
M = 0.35 ± 0.07 (this error
flag is ours; it is meant to indicate 95% certainty that
 M is between
0.2 and 0.5). The gravity
of dark matter is needed to hold together just about everything
in the Universe - galaxies, clusters of galaxies, superclusters
and the Universe itself. A variety of methods for determining
the amount of matter all seem to converge on
M is between
0.2 and 0.5). The gravity
of dark matter is needed to hold together just about everything
in the Universe - galaxies, clusters of galaxies, superclusters
and the Universe itself. A variety of methods for determining
the amount of matter all seem to converge on  M ~ 1/3;
they include measurements of the masses of clusters of
galaxies and the peculiar motions of galaxies. Finally, the
theory of big-bang nucleosynthesis and the recently measured
primeval abundance of deuterium pin down the baryon density
very precisely:
M ~ 1/3;
they include measurements of the masses of clusters of
galaxies and the peculiar motions of galaxies. Finally, the
theory of big-bang nucleosynthesis and the recently measured
primeval abundance of deuterium pin down the baryon density
very precisely:  B = (0.02 ± 0.002)
h-2
B = (0.02 ± 0.002)
h-2  0.05.
The discrepancy between this number and dynamical measurements
of the matter density is evidence for nonbaryonic dark matter.
0.05.
The discrepancy between this number and dynamical measurements
of the matter density is evidence for nonbaryonic dark matter.
Particle physics suggests three dark matter candidates (Sadoulet 1999): a 10-5 eV axion (Rosenberg 1998); a 10 Gev - 500 Gev neutralino (Jungman, Kamionkowski, and Griest 1996); and a 30 eV neutrino. These three possibilities are highly motivated in two important senses: first, the axion and neutralino are predictions of fundamental theories that attempt to go beyond the standard model of particle physics, as are neutrino masses; and second, the relic abundances of the axion and neutralino turn out to be within a factor of ten of the critical density - and similarly for the neutrino, GUTs predict masses in the eV range, which is what is required to make neutrinos a significant contributor to the mass density.
Because measuring the masses of galaxy clusters has been key to defining
the dark matter problems it is perhaps worth further discussion.
Cluster masses can be estimated by three
different techniques - which give consistent results. The first,
which dates back to
Fritz Zwicky (1935),
uses the measured velocities
of cluster galaxies and the virial theorem to determine the total
mass (i.e., KEgal  |PEgal|/2).
The second method uses the temperature of the hot x-ray
emitting intracluster gas and the virial theorem to arrive at the total
mass. The third and most direct method is using the gravitational
lensing effects of the cluster on much more distant galaxies.
Close to the cluster center, lensing is strong enough to produce
multiple images; farther out, lensing distorts the shape of distant
galaxies. The lensing method allows the cluster (surface) mass
density to be mapped directly. An example of mapping the mass
distribution of a cluster of galaxies is shown in
Fig. 8.
|PEgal|/2).
The second method uses the temperature of the hot x-ray
emitting intracluster gas and the virial theorem to arrive at the total
mass. The third and most direct method is using the gravitational
lensing effects of the cluster on much more distant galaxies.
Close to the cluster center, lensing is strong enough to produce
multiple images; farther out, lensing distorts the shape of distant
galaxies. The lensing method allows the cluster (surface) mass
density to be mapped directly. An example of mapping the mass
distribution of a cluster of galaxies is shown in
Fig. 8.
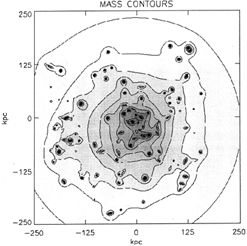
|
Figure 8. The reconstructed total mass
density in the
cluster of galaxies 0024+1654 at redshift z = 0.39, based on
parametric inversion of the associated gravitational lens.
Projected mass contours are spaced by 430 |
Using clusters to estimate the mean mass density of the Universe
requires a further assumption: that their mass-to-light ratio provides
a good estimate for the mean mass-to-light ratio. This is
because the mean mass density is determined by multiplying
the mean luminosity density (which is reasonably well measured)
by the inferred cluster mass-to-light ratio. Using this technique,
Carlberg et al.
(1996,
1997)
find  M = 0.19 ± 0.06 ± 0.04.
If clusters have more luminosity per mass than average, this technique
would underestimate
M = 0.19 ± 0.06 ± 0.04.
If clusters have more luminosity per mass than average, this technique
would underestimate  M.
M.
There is another way to estimate  M using clusters, based on
a different, more physically motivated assumption.
X-ray measurements more easily determine the amount of hot, intracluster
gas; and as it turns out, most the baryonic mass in a cluster resides
here rather than in the mass of individual galaxies (this fact is
also confirmed by lensing measurements). Together with the
total cluster mass, the ratio of baryonic mass to total mass
can be determined; a compilation of the existing data give
MB / MTOT = (0.07 ± 0.007)
h-3/2
M using clusters, based on
a different, more physically motivated assumption.
X-ray measurements more easily determine the amount of hot, intracluster
gas; and as it turns out, most the baryonic mass in a cluster resides
here rather than in the mass of individual galaxies (this fact is
also confirmed by lensing measurements). Together with the
total cluster mass, the ratio of baryonic mass to total mass
can be determined; a compilation of the existing data give
MB / MTOT = (0.07 ± 0.007)
h-3/2 0.15
(Evrard 1997
and references therein).
Assuming that clusters provide a fair sample of matter in the Universe so
that
0.15
(Evrard 1997
and references therein).
Assuming that clusters provide a fair sample of matter in the Universe so
that  B /
B /  M =
MB / MTOT, the accurate
BBN determination of
M =
MB / MTOT, the accurate
BBN determination of  B can be used to infer:
B can be used to infer:  M
= (0.3 ± 0.05) h-1/2
M
= (0.3 ± 0.05) h-1/2  0.4. [A similar result for
the cluster gas to total mass ratio is derived from cluster
gas measurements based upon the distortion of the CMB spectrum
due to CMB photons scattering off the hot cluster gas (Sunyaev - Zel'dovich
effect); see
Carlstrom 1999.]
0.4. [A similar result for
the cluster gas to total mass ratio is derived from cluster
gas measurements based upon the distortion of the CMB spectrum
due to CMB photons scattering off the hot cluster gas (Sunyaev - Zel'dovich
effect); see
Carlstrom 1999.]
Two other measurements bear on the quantity and composition of
energy and matter in the Universe. First, the pattern of anisotropy
in the CMB depends upon the total energy density in the
Universe (i.e.,  0)
(see e.g.,
Jungman,
Kamionkowski, Kosowsky and Spergel 1996).
The peak in the multipole
power spectrum is lpeak
0)
(see e.g.,
Jungman,
Kamionkowski, Kosowsky and Spergel 1996).
The peak in the multipole
power spectrum is lpeak  200 / sqrt(
200 / sqrt( 0). The current data, shown in
Fig. 5,
are consistent with
0). The current data, shown in
Fig. 5,
are consistent with  0
0
 1, though
1, though  0 ~ 0.3 cannot be excluded. This
together with the evidence that
0 ~ 0.3 cannot be excluded. This
together with the evidence that  M
M  0.3
leaves room for a component of energy that does not clump, such
as a cosmological constant.
0.3
leaves room for a component of energy that does not clump, such
as a cosmological constant.
The oldest approach to determining the total mass-energy density is through the deceleration parameter (Baum 1957; Sandage 1961), which quantifies the present slowing of the expansion due to gravity,
where subscript zero refers to quantities measured at the current epoch.
Note, in a Universe where the bulk of the matter is nonrelativistic
(p
and thus accurate distance measurements can be used to determine
q0.
(The luminosity distance to an object is defined as that inferred from
the inverse square law: dL
Recently, two groups (The Supernova
Cosmology Project and The High-z Supernova Team) using Type Ia supernovae
(SNe1a) as standard candles (objects of known
Pulling this together, cosmologists for the
first time have a plausible accounting of matter
and energy in the Universe: stars contribute around 0.4%
of the critical density, baryons contribute 5%, nonrelativistic
particles of unknown type contribute 30%,
and vacuum energy contributes 64%,
for a total equaling the critical density (see
Figures 9
and 10).
We should emphasize that plausible does not mean correct.
In addition to the fact that most of the matter and energy
in the Universe is dark, most of the ordinary matter is dark
(i.e., not in bright stars). The possibilities for the dark baryons
include ``dark stars'' and diffuse hot or warm gas (recall,
in clusters, most of the baryons are in hot, intracluster gas).
Dark stars could take the form of faint, low-mass stars, failed stars
(i.e., objects below the mass required for hydrogen burning,
M
Most of the mass of our own Milky Way galaxy is dark, existing
in an extended halo (an approximately spherical distribution
of matter with density falling as 1 / r2). Unsuccessful
searches for faint stars in our galaxy have eliminated them
as a viable candidate, and theoretical arguments disfavor
white dwarfs, black holes and neutron stars - all should
lead to the production of more heavy elements than are observed.
Further, the measured rate of star formation indicates that
only a fraction of the baryons have formed into bright, massive stars.
Experimental searches for dark stars in our own galaxy have been
carried out using the gravitational microlensing technique:
dark stars along the line of sight to nearby
galaxies (e.g., the Large and Small Magellanic Clouds
and Andromeda) can gravitationally lens the distant bright
stars, causing a well-defined temporary brightening
(Paczynski 1986).
The results, however, are perplexing (see e.g.,
Sadoulet 1999).
More than a dozen such brightenings of LMC stars have been seen, suggesting
that a significant fraction of our galaxy's halo exists
in the form of half-solar mass white dwarfs. However, such
a population of white dwarfs should be visible,
and they have not been seen. Because of our imperfect
knowledge of our own galaxy and the LMC, it is possible that
the lenses are not associated with the halo of our galaxy but
rather are low-mass stars in the LMC, in an intervening
dwarf galaxy in between, or are actually in
the disk of our galaxy, if the disk is warped enough to pass
in front of the line to the LMC.
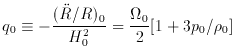
 ),
q0 and
),
q0 and  0 differ only by a factor of two.
The luminosity distance to an object at redshift z << 1 is related
to q0,
0 differ only by a factor of two.
The luminosity distance to an object at redshift z << 1 is related
to q0,
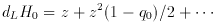
 sqrt(
sqrt( / 4
/ 4
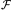 .)
.)
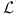 ) and
assuming that their flux measurements (i.e.,
) and
assuming that their flux measurements (i.e., 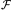 )
were not contaminated by sample selection, evolution, or dust systematics,
both conclude that the expansion of the Universe
is accelerating rather than decelerating (i.e., q0 < 0)
(Perlmutter et al. 1998;
Schmidt et al. 1998).
If correct, this implies that much of the energy in the Universe
is in an unknown component, with negative pressure, pX
)
were not contaminated by sample selection, evolution, or dust systematics,
both conclude that the expansion of the Universe
is accelerating rather than decelerating (i.e., q0 < 0)
(Perlmutter et al. 1998;
Schmidt et al. 1998).
If correct, this implies that much of the energy in the Universe
is in an unknown component, with negative pressure, pX
 -
- X / 3
(Garnavich et al. 1998).
The simplest explanation is a cosmological constant with
X / 3
(Garnavich et al. 1998).
The simplest explanation is a cosmological constant with

 ~ 2/3.
(In fact, Equ. 10, which is deeply rooted
in the history of cosmology, is not sufficiently accurate at the
redshifts of the SNe1a being used, and the two groups compute
dL
~ 2/3.
(In fact, Equ. 10, which is deeply rooted
in the history of cosmology, is not sufficiently accurate at the
redshifts of the SNe1a being used, and the two groups compute
dL  (1 +
z)r(z) as a function of
(1 +
z)r(z) as a function of  M and
M and 
 and fit to the observations.)
and fit to the observations.)
 0.08
M
0.08
M ), white dwarfs, neutron stars or black holes.
), white dwarfs, neutron stars or black holes.