8.2 Present Status of Inflation + CDM

A useful way to organize the different CDM models is by their dark matter content; within each CDM family, the cosmological parameters can still vary: sCDM (for simple), only CDM and baryons; CDM: in addition to CDM and baryons additional radiation (e.g., produced by the decay of an unstable massive tau neutrino); CDM: CDM, baryons, and a dash of hot dark matter (e.g., = 0.2); and CDM: CDM, baryons, and a cosmological constant (e.g., = 0.6). In all these models, the total energy density sums to the critical energy density; in all but CDM, _M = 1.

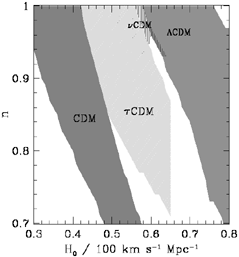
Figure 13. Acceptable cosmological parameters for different CDM models, as are characterized by their invisible matter content: simple CDM (CDM), CDM plus cosmological constant (CDM), CDM plus some hot dark matter (CDM), and CDM plus added relativistic particles (CDM) (from Dodelson et al. 1996).

Figure 13 summarizes the viability of these different CDM models, based upon CMB measurements and current determinations of the present power spectrum of fluctuations (derived from redshift surveys; see Fig. 14). sCDM is only viable for low values of the Hubble constant (less than 55 km s^-1 Mpc^-1) and/or significant tilt (deviation from scale invariance); the region of viability for CDM is similar to sCDM, but shifted to larger values of the Hubble constant (as large as 65 km s^-1 Mpc^-1). CDM has an island of viability around H₀ 60 km s^-1 Mpc^-1and n 0.95. CDM can tolerate the largest values of the Hubble constant.

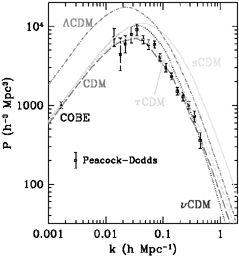
Figure 14. The power spectrum of fluctuations today, as traced by bright galaxies (light), as derived from redshift surveys assuming light traces mass (Peacock and Dodds 1994). The curves correspond to the predictions of various cold dark matter models. The relationship between the power spectrum and CMB anisotropy in a CDM model is different, and in fact, the CDM model shown is COBE normalized.

Considering other relevant data too - e.g., age of the Universe, determinations of _M, measurements of the Hubble constant, and limits to - CDM emerges as the ``best-fit CDM model'' (see e.g., Krauss & Turner 1995; Ostriker & Steinhardt 1995). Moreover, its ``key signature,'' q₀ ~ -0.5, may have been confirmed. Given the possible systematic uncertainties in the SNe1a data and other measurements, it is premature to conclude that CDM is anything but the model to take aim at!