


8.1 Testing Inflation + CDM in the Precision Era
As we look forward to the abundance (avalanche!) of high-quality observations that will test Inflation + CDM, we have to make sure the predictions of the theory match the precision of the data. In so doing, CDM + Inflation becomes a theory with ten or more parameters. For cosmologists, this is a bit daunting, as it may seem that a ten-parameter theory can be made to fit any set of observations. This will not be the case when one has the quality and quantity of data that are coming. The standard model of particle physics offers an excellent example: it is a 19-parameter theory, and because of the high quality of data from experiments at high-energy accelerators and other facilities, it has been rigorously tested, with parameters measured to a precision of better than 1% in some cases.
In fact, the ten parameters of CDM + Inflation are an opportunity rather than a curse: Because the parameters depend upon the underlying inflationary model and fundamental aspects of the Universe, we have the very real possibility of learning much about the Universe, inflation, and perhaps fundamental physics. The ten parameters can be split into two groups: cosmological and dark matter.
h, the Hubble constant in units of 100km s-1 Mpc-1.
 Bh2, the baryon density.
Bh2, the baryon density.
n, the power-law index of the scalar
density perturbations.
CMB measurements indicate n = 1.1 ± 0.2; n = 1
corresponds to scale-invariant density perturbations. Several popular
inflationary models predict n  0.95; range of predictions runs from 0.7 to 1.2.
0.95; range of predictions runs from 0.7 to 1.2.
dn / dlnk, ``running'' of the scalar
index with comoving scale
(k = wavenumber). Inflationary models predict a value of
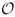 (±
10-3) or smaller.
(±
10-3) or smaller.
S, the overall amplitude squared of density perturbations, quantified by their contribution to the variance of the quadrupole CMB anisotropy.
T, the overall amplitude squared of gravitational waves, quantified by their contribution to the variance of the quadrupole CMB anisotropy. Note, the COBE normalization determines T + S (see below).
nT, the power-law index of the gravitational wave spectrum. Scale invariance corresponds to nT = 0; for inflation, nT is given by -T / 7S.

 , the fraction of critical density
in neutrinos (=
, the fraction of critical density
in neutrinos (=  i m
i m
 X, the fraction of critical density in a
smooth component
of unknown composition and negative pressure (wX
X, the fraction of critical density in a
smooth component
of unknown composition and negative pressure (wX  -0.3); the
simplest example is a cosmological constant (wX = -1).
-0.3); the
simplest example is a cosmological constant (wX = -1).
g*, the quantity that counts the number of ultra-relativistic degrees of freedom (at late times). The standard cosmology/standard model of particle physics predicts g* = 3.3626 (photons in the CMB + 3 massless neutrino species with temperature (4/11)1/3 times that of the photons). The amount of radiation controls when the Universe becomes matter-dominated and thus affects the present spectrum of density fluctuations.
The parameters involving density and gravitational-wave perturbations depend directly upon the inflationary potential. In particular, they can be expressed in terms of the potential and its first two derivatives (see e.g., Lidsey et al. 1997):
where V(
As particle physicists can testify, testing a ten (or more) parameter
theory is a long, but potentially rewarding process. To begin, one has
to test the basic tenets and consistency of the underlying theory.
Only then, can one proceed to take
full advantage of the data to precisely measure parameters of the theory.
The importance of establishing a theoretical framework is illustrated
by measurements of the number of light neutrino species derived from
the decay width of the Z0 boson: N
In the present case, the putative theoretical framework
is Inflation + CDM, and its basic tenets are: a flat, critical
density Universe;
a nearly scale-invariant spectrum of Gaussian density perturbations;
and a stochastic background of gravitational waves. The first two
predictions are much more amenable to testing, by a combination of
CMB anisotropy and large-scale structure measurements. For example,
a flat Universe with Gaussian curvature perturbations implies a multipole
power spectrum of well defined acoustic peaks, beginning at l
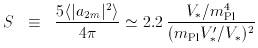
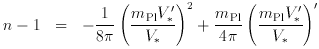
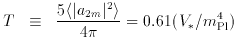
 ) is the
inflationary potential, prime denotes d / d
) is the
inflationary potential, prime denotes d / d ,
and V* is the value of the scalar potential when the
present horizon scale crossed outside the horizon during inflation.
,
and V* is the value of the scalar potential when the
present horizon scale crossed outside the horizon during inflation.
 = 3.07 ± 0.12 (not assuming
the correctness of the standard model); N
= 3.07 ± 0.12 (not assuming
the correctness of the standard model); N = 2.994 ± 0.012
(assuming the correctness of the standard model).
= 2.994 ± 0.012
(assuming the correctness of the standard model).
 200 (see Fig. 5). In addition, there
are consistency tests:
comparison of the precise BBN determination of the baryon density with
that derived from CMB anisotropy; an accounting of the dark matter and
dark energy by gravitational lensing; SNe1a measurements of acceleration;
and comparison of the different determinations of the Hubble constant.
Once the correctness and consistency of Inflation + CDM has been verified -
assuming it is - one can zero in on the remaining parameters (subset
of the list above) and hope to determine them with precision.
200 (see Fig. 5). In addition, there
are consistency tests:
comparison of the precise BBN determination of the baryon density with
that derived from CMB anisotropy; an accounting of the dark matter and
dark energy by gravitational lensing; SNe1a measurements of acceleration;
and comparison of the different determinations of the Hubble constant.
Once the correctness and consistency of Inflation + CDM has been verified -
assuming it is - one can zero in on the remaining parameters (subset
of the list above) and hope to determine them with precision.