


4.1 ANISOTROPIC RADIATION FROM RELATIVISTIC BEAMING
When an emitting plasma has a bulk relativistic motion relative to a fixed
observer, its emission is beamed in the forward direction (in the fixed
frame), a direct consequence of the
transformation of angles in special relativity. An observer
located in or near the path of such a plasma sees much more
intense emission than if the same plasma were at rest. Time
scales for variability are also shorter, and this can cause the
emission region to appear to move superluminally in the
transverse direction
(Appendix A). Strong relativistic
beaming is thought
to explain the rapid variations, high polarization, and high
luminosities that characterize blazars
(Blandford and Rees
1978),
and if present in blazars, it must also be present in other radio-loud
AGN. The consequences of the anisotropic beamed radiation pattern are
considerable (Appendices B and
C),
introducing significant selection effects in almost any flux-limited
sample.
4.1 Evidence for Relativistically Beamed
Gamma-Rays
More than forty blazars have now been detected with the EGRET high
energy experiment on the Compton Gamma-Ray Observatory
(von Montigny et
al. 1995).
Without exception, all EGRET-detected extragalactic objects are
radio-loud blazars, either FSRQ or BL Lac objects (primarily the former). Not
only are blazars bright at E  100 MeV, in many cases their observed
gamma-ray luminosity dominates the luminosity in other wavebands by a factor
between 1 and 1000.
Multiwavelength spectra of the superluminal quasar 3C 279
(Fig. 4) show that the
ratio of gamma-ray to bolometric luminosity increases with overall luminosity
(Maraschi et
al. 1994a).
100 MeV, in many cases their observed
gamma-ray luminosity dominates the luminosity in other wavebands by a factor
between 1 and 1000.
Multiwavelength spectra of the superluminal quasar 3C 279
(Fig. 4) show that the
ratio of gamma-ray to bolometric luminosity increases with overall luminosity
(Maraschi et
al. 1994a).
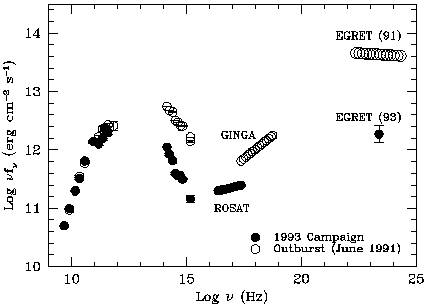
|
| Figure 4. Multiwavelength spectra of the gamma-ray-bright
superluminal quasar 3C 279
(Maraschi et
al. 1994a)
at two epochs, a high state in June 1991 and a low state in January
1993. In the high state, the
gamma-ray luminosity is ten times the luminosity in the synchrotron
component seen at lower energies, while in the low state the two are
comparable.
(Copyright American Astronomical Society, reproduced with permission.
|
In several blazars, the observed high-energy gamma-rays are highly variable,
on time scales of a few days. (6) For example, the intensity of 3C 279
(z = 0.538) declined by a factor of 4-5 in less than 3 days
(Fig. 5;
Kniffen et al. 1993),
and the blazar PKS 0528+134 (z = 2.06) more than doubled
its intensity in 5 days
(Hunter et al. 1993).
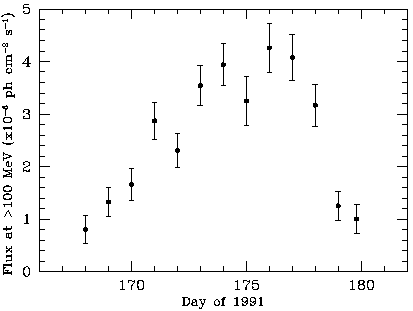
|
| Figure 5. Gamma-ray light curve of the superluminal quasar
3C 279 during
the bright outburst in June 1991
(Kniffen et al. 1993).
The combination of
rapid variability and high gamma-ray luminosity strongly suggests the
emission is relativistically beamed.
(Copyright American Astronomical Society, reproduced with permission.)
|
This rapid variability leads to a largely model-independent argument that the
gamma-rays, at least, must be relativistically beamed
(Maraschi et al. 1992).
This argument does not depend on which physical mechanism gives rise to the
gamma-ray emission, simply on the observed luminosity and variability time
scales at high energies. Specifically, in order for gamma-rays to escape
the source, the optical depth to pair production, 

 , must
be of order unity or less, which is equivalent to saying the compactness, a
convenient dimensionless parameter that represents source luminosity divided
by dimension, must be less than about 40 at the threshold for pair-production.
That is,
, must
be of order unity or less, which is equivalent to saying the compactness, a
convenient dimensionless parameter that represents source luminosity divided
by dimension, must be less than about 40 at the threshold for pair-production.
That is, 

 ~
~
 / 40 << 1, where
/ 40 << 1, where  = (L/r)
(
= (L/r)
( T / mec3) is the
compactness, L and r are the source luminosity and dimension,
respectively, and me and c are the usual
constants (electron mass and
speed of light). The Thomson cross section,
T / mec3) is the
compactness, L and r are the source luminosity and dimension,
respectively, and me and c are the usual
constants (electron mass and
speed of light). The Thomson cross section,  T, is appropriate because
most pairs will be produced by X-
T, is appropriate because
most pairs will be produced by X- interactions.
interactions.
For 3C 279 and PKS 0528+134, the inferred values for the
compactness are 5000 to 15,000,
well in excess of the optical depth limit. In order that we
observe gamma-rays from these blazars, the true gamma-ray luminosity,
 , must be much smaller than
observed and the true dimension much larger.
Relativistic beaming has the effect that Lobs =
, must be much smaller than
observed and the true dimension much larger.
Relativistic beaming has the effect that Lobs =
 4
4  [Eq. (B5)], where
[Eq. (B5)], where  is the
Doppler beaming factor
(Appendix A). If r is estimated
from the variability time scale
(r ~
is the
Doppler beaming factor
(Appendix A). If r is estimated
from the variability time scale
(r ~  c
c  t), then
t), then
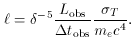 (1)
(1)
The limit 
 40 then translates to
40 then translates to 
 6 for 3C 279 and
6 for 3C 279 and 
 7 for PKS 0528+134, where
Lobs has been evaluated at X-ray energies under
reasonable spectral assumptions
(Maraschi et al. 1992);
similar limits are obtained for all the gamma-ray blazars
(Dondi and
Ghisellini 1995).
For comparison, the values derived in an entirely independent
way from a synchrotron self-Compton calculation using radio
and X-ray data (see Sec. 4.4) are
7 for PKS 0528+134, where
Lobs has been evaluated at X-ray energies under
reasonable spectral assumptions
(Maraschi et al. 1992);
similar limits are obtained for all the gamma-ray blazars
(Dondi and
Ghisellini 1995).
For comparison, the values derived in an entirely independent
way from a synchrotron self-Compton calculation using radio
and X-ray data (see Sec. 4.4) are  18 for 3C 279 and
3 for PKS 0528+134
(Ghisellini et
al. 1993).
18 for 3C 279 and
3 for PKS 0528+134
(Ghisellini et
al. 1993).
Note that no radio-quiet AGN have been detected so far with
EGRET. One cannot rule out that, since gamma-ray power
appears to correlate with radio power
(Padovani et al. 1993),
radio-quiet AGN might still have blazar-like spectra with
high-energy (> 50 MeV) emission well below the sensitivity
of EGRET. This is unlikely, however, because OSSE
observations of Seyfert 1 galaxies show steep cutoffs above
~ 50 keV, in sharp contrast to the hard spectra of
radio-loud objects
(Kurfess et al. 1994).
The difference in gamma-ray
properties may then be related to radio-loudness, which in turn must be closely
associated with relativistic beaming.
6 The variability time scale can
be defined in several ways, including the doubling time
[td = < F > (dF/dt)-1] or the
e-folding time [te = (dln F /
dt)-1]. Either is fine for the rough
estimates here as long as it is derived from a substantial change
in flux ( 30%). Back.
30%). Back.



 100 MeV, in many cases their observed
gamma-ray luminosity dominates the luminosity in other wavebands by a factor
between 1 and 1000.
Multiwavelength spectra of the superluminal quasar 3C 279
(Fig. 4) show that the
ratio of gamma-ray to bolometric luminosity increases with overall luminosity
(Maraschi et
al. 1994a).
100 MeV, in many cases their observed
gamma-ray luminosity dominates the luminosity in other wavebands by a factor
between 1 and 1000.
Multiwavelength spectra of the superluminal quasar 3C 279
(Fig. 4) show that the
ratio of gamma-ray to bolometric luminosity increases with overall luminosity
(Maraschi et
al. 1994a).







 / 40 << 1, where
/ 40 << 1, where  T / mec3) is the
compactness, L and r are the source luminosity and dimension,
respectively, and me and c are the usual
constants (electron mass and
speed of light). The Thomson cross section,
T / mec3) is the
compactness, L and r are the source luminosity and dimension,
respectively, and me and c are the usual
constants (electron mass and
speed of light). The Thomson cross section,  , must be much smaller than
observed and the true dimension much larger.
Relativistic beaming has the effect that Lobs =
, must be much smaller than
observed and the true dimension much larger.
Relativistic beaming has the effect that Lobs =
 4
4  t), then
t), then
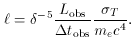
 40 then translates to
40 then translates to  6 for
6 for