


5.6 Effect of Relativistic Beaming on Number Statistics
AGN with anisotropic emission patterns will be boosted into and shifted out of
flux-limited samples according to their orientation. For some radiation
patterns, including those caused by relativistic beaming
(Urry and Shafer 1984)
and thick accretion disks
(Urry et al. 1991b),
a narrow distribution in
intrinsic luminosity is broadened into a flat distribution over a wide range
of observed luminosities (which follows from the probability function for flux
enhancement.) This leads to a distortion in the measured shape of the
luminosity function of the boosted AGN relative to their intrinsic luminosity
function
(Urry and Shafer 1984;
Urry and Padovani
1991).
More specifically, under the basic assumption that AGN are randomly oriented
on the sky, and assuming a radiation pattern, we can predict the exact numbers
of AGN with a given observed luminosity relative to their intrinsic luminosity
(summed over all angles). Given the luminosity function (LF) of the misaligned
AGN, then, one can predict the LF of the aligned AGN, subject to the form of
the radiation pattern. In practice, the pattern for relativistic beaming
depends on the assumed distribution of Lorentz factors and on whether one
assumes a uni-directional jet or a fan beam; the pattern for obscuration
depends on the size and optical depth of the torus; the pattern for thick
disks depends primarily on the funnel geometry.
To evaluate the number statistics of radio-loud unification schemes we
incorporate the effect of relativistic beaming on the observed LFs
(Urry and Shafer 1984).
Consider an ensemble of emitters all having the same intrinsic
luminosity ( ) and all moving
with the same relativistic bulk speed
(
) and all moving
with the same relativistic bulk speed
( ) at random angles
(
) at random angles
( ) to the line of sight.
Given that L =
) to the line of sight.
Given that L =  p
p  [Eq. (B7)], the probability of
having a particular Doppler factor
[Eq. (B7)], the probability of
having a particular Doppler factor  = [
= [ (1
-
(1
-  cos
cos )]-1
(Appendix A) is P(
)]-1
(Appendix A) is P( ) = d (cos
) = d (cos ) / d
) / d  = (
= (

 2)-1. The
probability of observing luminosity L given intrinsic (emitted)
luminosity
2)-1. The
probability of observing luminosity L given intrinsic (emitted)
luminosity  is
is
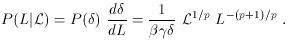 (4)
(4)
For fixed  , the distribution
of observed luminosities
is a flat power law (with index in the range 1-1.5 for likely values of
p; Appendix B) extending from L
~ (2
, the distribution
of observed luminosities
is a flat power law (with index in the range 1-1.5 for likely values of
p; Appendix B) extending from L
~ (2 )-p
)-p  to L ~
(2
to L ~
(2 )p
)p  . The observed luminosity distributions are illustrated
in Fig. 13(a) (thick dashed lines) for three
different intrinsic
luminosities (thin dashed lines). The low-luminosity cutoff corresponds to an
emitter moving directly away from us (
. The observed luminosity distributions are illustrated
in Fig. 13(a) (thick dashed lines) for three
different intrinsic
luminosities (thin dashed lines). The low-luminosity cutoff corresponds to an
emitter moving directly away from us ( = 180°) and the
high-luminosity cutoff to an approaching emitter perfectly aligned (
= 180°) and the
high-luminosity cutoff to an approaching emitter perfectly aligned ( =
0°). The normalization of this flat power law decreases with increasing
beaming (higher
=
0°). The normalization of this flat power law decreases with increasing
beaming (higher  ,
,
 , or p)
because the beaming cone angle gets smaller.
, or p)
because the beaming cone angle gets smaller.

|
|
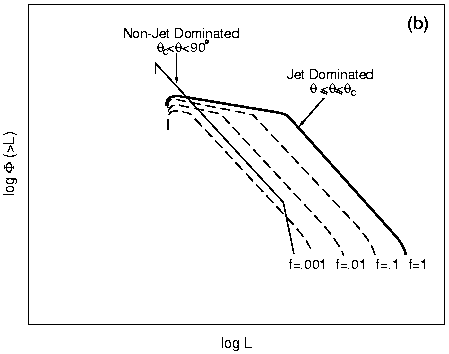
Figure 13. The effect of relativistic beaming on observed
luminosity functions.
(a) Simple case where all emitted flux comes from a randomly oriented
relativistic jet. For a delta-function intrinsic luminosity
(thin dashed line), the observed luminosity function after beaming
(thick dashed line) is a flat power law of differential slope
1  (p + 1) /
p (p + 1) /
p  1.5 (Eq. 4). A
power-law intrinsic luminosity function (thin solid line), after
integration of Eq. (5), gives rise to an observed luminosity function that is
a double power law (thick solid line), with flat slope (p
+ 1) / p at low luminosities and the same slope as the intrinsic
power law at high luminosities. (b) Case where the intrinsic luminosity
in the jet is a fraction f = 0.001, 0.01, 0.1, or 1 of the
unbeamed luminosity. As in (a), the beamed
luminosity function has slope (p + 1) / p below the break
and the parent
luminosity function slope above the break. In both (a) and (b), the high
luminosity objects (those in the steep part of the beamed luminosity function)
are oriented close to the line of sight ( 1.5 (Eq. 4). A
power-law intrinsic luminosity function (thin solid line), after
integration of Eq. (5), gives rise to an observed luminosity function that is
a double power law (thick solid line), with flat slope (p
+ 1) / p at low luminosities and the same slope as the intrinsic
power law at high luminosities. (b) Case where the intrinsic luminosity
in the jet is a fraction f = 0.001, 0.01, 0.1, or 1 of the
unbeamed luminosity. As in (a), the beamed
luminosity function has slope (p + 1) / p below the break
and the parent
luminosity function slope above the break. In both (a) and (b), the high
luminosity objects (those in the steep part of the beamed luminosity function)
are oriented close to the line of sight ( ~ 0°). ~ 0°).
|
For a distribution of intrinsic luminosities (i.e., a luminosity function),
the observed LF is just the integral of the intrinsic luminosity distribution
times the conditional probability function in Eq. (4):
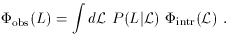 (5)
(5)
This integral [thick solid line in Fig. 13(a)]
is basically the envelope of the beamed LFs for fixed intrinsic
luminosities (the intrinsic LF is shown as a thin solid line). For
simple power law luminosity functions, Eq. (5) can be integrated analytically
(Urry and Shafer
1984).
In practice, one expects an unbeamed component (e.g., radio lobes) to be
present in addition to a beamed component (jet). We use the simple
parametrization that the intrinsic luminosity in the jet is a fixed fraction
of the unbeamed luminosity,  j = f
j = f  u, so the total observed luminosity is
u, so the total observed luminosity is
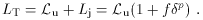 (6)
(6)
This takes account of the approaching jet only; it can be shown that if jets
come in oppositely directed pairs of similar intrinsic power,
the receding beamed component (with
Doppler factor equal to  =
[
=
[ (1 +
(1 +  cos
cos
 )]-1) will
have a negligible contribution for likely values of the Lorentz factor and
approaching jets within ~ 60° of the line of sight
(Appendix C).
As before, the
conditional probability is derived from Eq. (6) but in this case
Eq. (5) is integrated numerically. A (likely) distribution of
Lorentz factors can also be included
(Urry and Padovani
1991).
If we define the critical angle,
)]-1) will
have a negligible contribution for likely values of the Lorentz factor and
approaching jets within ~ 60° of the line of sight
(Appendix C).
As before, the
conditional probability is derived from Eq. (6) but in this case
Eq. (5) is integrated numerically. A (likely) distribution of
Lorentz factors can also be included
(Urry and Padovani
1991).
If we define the critical angle,
 c, to be
where the beamed and unbeamed luminosities are
comparable (i.e., f
c, to be
where the beamed and unbeamed luminosities are
comparable (i.e., f  p = 1), then for
p = 1), then for  <
<  c the
luminosity will be dominated by beamed emission and we can identify these
sources as blazars. The observed parent and beamed LFs for the case of a
single-power-law intrinsic LF are shown in
Fig. 13(b), for four values of f.
c the
luminosity will be dominated by beamed emission and we can identify these
sources as blazars. The observed parent and beamed LFs for the case of a
single-power-law intrinsic LF are shown in
Fig. 13(b), for four values of f.
The key point is that the luminosity function of the beamed population has a
characteristic broken-power-law form, flat at the low luminosity end and steep
at the high luminosity end
(Urry and Shafer
1984).
This remains approximately the case even when the
intrinsic luminosity function has a more complicated form, without sharp
cutoffs
(Urry and Padovani
1991).
This means that the comparison of the number
densities of beamed and parent populations is a strong function of luminosity,
and for samples biased by relativistic beaming
can be evaluated only by measuring the luminosity functions for each.
Since radio maps of blazars show the presence of a diffuse component we
consider the two-component model for which LT =
 (1 + f
(1 + f  p) (Eq. 6). The assumption that the
intrinsic jet
power is linearly proportional to the extended power may not be consistent
with observations. Observed core power and total radio power are well
correlated but apparently not linearly
(Feretti et al. 1984;
Giovannini et al. 1988;
Jones et al. 1994).
Although results vary, all seem to find that observed core
power has a less than linear dependence on total radio power. (Since their
samples include mainly radio galaxies, total power is essentially the same as
extended power.) For example,
Jones et al. (1994)
find that
Pcore
p) (Eq. 6). The assumption that the
intrinsic jet
power is linearly proportional to the extended power may not be consistent
with observations. Observed core power and total radio power are well
correlated but apparently not linearly
(Feretti et al. 1984;
Giovannini et al. 1988;
Jones et al. 1994).
Although results vary, all seem to find that observed core
power has a less than linear dependence on total radio power. (Since their
samples include mainly radio galaxies, total power is essentially the same as
extended power.) For example,
Jones et al. (1994)
find that
Pcore  P0.8total. The range of observed slopes,
generally calculated taking upper limits into account, is
0.4-0.8. Calculating the
regression with Pcore as the dependent parameter will
lead to a systematically different slope and indeed treating the
variables symmetrically would be the appropriate approach
(Isobe et al. 1990).
P0.8total. The range of observed slopes,
generally calculated taking upper limits into account, is
0.4-0.8. Calculating the
regression with Pcore as the dependent parameter will
lead to a systematically different slope and indeed treating the
variables symmetrically would be the appropriate approach
(Isobe et al. 1990).
We note that the observed nonlinearity does not immediately conflict with the
assumption that  jet = f
jet = f  ext. First, beaming
will cause large scatter in the observed Pc -
Pext plane due
to the spread in viewing angles and possibly Lorentz factors. Second,
selection effects could influence the slope of the correlation, although we do
not immediately see why it should be flatter than unity. If the intrinsic
relation is nonlinear (e.g.,
ext. First, beaming
will cause large scatter in the observed Pc -
Pext plane due
to the spread in viewing angles and possibly Lorentz factors. Second,
selection effects could influence the slope of the correlation, although we do
not immediately see why it should be flatter than unity. If the intrinsic
relation is nonlinear (e.g.,  jet = f
jet = f  xext),
then the calculation described here [represented by Eqs. (5) and
(6)] would need to be modified. This would change the
derived parameter values but as long as x is reasonably close to 1, it
should not be a major effect.
xext),
then the calculation described here [represented by Eqs. (5) and
(6)] would need to be modified. This would change the
derived parameter values but as long as x is reasonably close to 1, it
should not be a major effect.
Radio-loud unification schemes, which involve primarily relativistic beaming,
have been verified with the luminosity function approach just described.
Radio-quiet schemes have not been tested this way because the radiation
patterns are still very uncertain and the radiation anisotropy is probably much
more Draconian at the usual (blue) selection wavelengths
(Pier and Krolik 1992;
Ward et al. 1991;
Djorgovski et
al. 1991).
For the
high-power radio-loud scheme, obscuration is needed to explain the optical
properties (namely, to allow for the fact that we do not have a direct view of
the broad line region in FR II radio galaxies)
but it is not important for statistical arguments based on
radio luminosities alone. In the next section we outline the quantitative
evaluation of the observed and beamed luminosity functions for radio-loud
AGN.



 ) and all moving
with the same relativistic bulk speed
(
) and all moving
with the same relativistic bulk speed
( ) at random angles
(
) at random angles
( ) to the line of sight.
Given that L =
) to the line of sight.
Given that L =  p
p  [Eq. (B7)], the probability of
having a particular Doppler factor
[Eq. (B7)], the probability of
having a particular Doppler factor  = [
= [ (1
-
(1
-  cos
cos )]-1
(Appendix A) is P(
)]-1
(Appendix A) is P( ) = d (cos
) = d (cos ) / d
) / d  = (
= (

 2)-1. The
probability of observing luminosity L given intrinsic (emitted)
luminosity
2)-1. The
probability of observing luminosity L given intrinsic (emitted)
luminosity  is
is



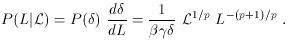


 (p + 1) /
p
(p + 1) /
p 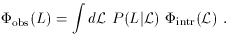
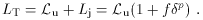
 P0.8total. The range of observed slopes,
generally calculated taking upper limits into account, is
0.4-0.8. Calculating the
regression with Pcore as the dependent parameter will
lead to a systematically different slope and indeed treating the
variables symmetrically would be the appropriate approach
(
P0.8total. The range of observed slopes,
generally calculated taking upper limits into account, is
0.4-0.8. Calculating the
regression with Pcore as the dependent parameter will
lead to a systematically different slope and indeed treating the
variables symmetrically would be the appropriate approach
(