


6.1.3 Beamed LFs of High-Luminosity Radio Sources
The beaming calculation is as follows. We start with the derived parent
luminosity function, then calculate the effect of beaming it
[Eqs. (4)-(6)]) adjusting free parameters
 (the Lorentz factor) and
f (the fraction of luminosity intrinsic to
the jet) to match the observed luminosity function of FSRQ. It was
not possible to fit the observed FSRQ luminosity function with a single
Lorentz factor; it required instead a distribution in the range 5
(the Lorentz factor) and
f (the fraction of luminosity intrinsic to
the jet) to match the observed luminosity function of FSRQ. It was
not possible to fit the observed FSRQ luminosity function with a single
Lorentz factor; it required instead a distribution in the range 5 

 40, weighted toward low
values: n (
40, weighted toward low
values: n ( )
) 
 -2.3, with a mean
value <
-2.3, with a mean
value <  >
>  11 and
f
11 and
f  5 x 10-3.
[Note that this last parameter is fixed by the
largest
5 x 10-3.
[Note that this last parameter is fixed by the
largest  and by the maximum
value of the ratio between beamed and unbeamed radio flux, R;
Eq. (C5).]
and by the maximum
value of the ratio between beamed and unbeamed radio flux, R;
Eq. (C5).]
Figure 14 shows the
beamed (solid line) and observed (filled circles) radio LFs of FSRQ, which
are in very good agreement. The ratio between FSRQ and parents, integrated
over the full luminosity function assuming that of the FR IIs cuts off at the
low luminosity end, is ~ 2%. (Because of the flat LF slope at low
luminosities, this percentage is not too sensitive to the cutoff.)
The critical angle separating FSRQ from SSRQ and FR IIs (15) is  c(
c( 1) ~
14°. The fitted parameters of
this beaming model are summarized in Table 3.
1) ~
14°. The fitted parameters of
this beaming model are summarized in Table 3.
Table 3. Beaming Model Parameters
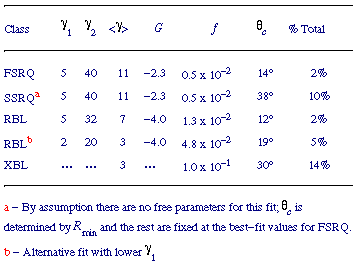
According to the beaming hypothesis, the steep-spectrum radio quasars are
supposed to be at intermediate angles and their intrinsic properties - in
particular, the value(s) of  and f - must be identical to those of
the FSRQ. Therefore, these parameters are already fixed.
The method of calculation is similar to the one used in the previous section;
however, since SSRQ are supposed to be misaligned objects,
and f - must be identical to those of
the FSRQ. Therefore, these parameters are already fixed.
The method of calculation is similar to the one used in the previous section;
however, since SSRQ are supposed to be misaligned objects,  min
min
 0°. We take
0°. We take  min = 14°, and
the observed value of Rmin ~ 0.002 is
used to constrain
min = 14°, and
the observed value of Rmin ~ 0.002 is
used to constrain  max for SSRQ [Eq. (C4)]).
With no free parameters, then,
we calculate the beamed luminosity function of SSRQ.
max for SSRQ [Eq. (C4)]).
With no free parameters, then,
we calculate the beamed luminosity function of SSRQ.
The comparison between observations (open triangles) and the
beaming model (dashed line) for SSRQ is shown in
Fig. 14. The agreement is quite
good, especially considering
we did not adjust the parameters to optimize the FSRQ and SSRQ fits jointly.
The angle dividing SSRQ from FR IIs is  ~ 38° (Table 3).
~ 38° (Table 3).
The same distribution of Lorentz factors produces a good fit to both the
luminosity functions of FSRQ and SSRQ. The value of  ~ 38°
for the angle separating SSRQ from FR II galaxies is in reasonable agreement
with the angle derived from the number density ratio in the observed range
of overlapping luminosity,
~ 38°
for the angle separating SSRQ from FR II galaxies is in reasonable agreement
with the angle derived from the number density ratio in the observed range
of overlapping luminosity,  =
arccos (1 + 1/6.4)-1
=
arccos (1 + 1/6.4)-1  30°.
The latter estimate is valid only when dealing with unbeamed
luminosities or (in
an approximate way) when the effect of beaming is not very strong because the
objects are viewed off-axis, as in this case.
For the 3CR sample, in which beaming is unimportant,
Barthel (1989)
found
30°.
The latter estimate is valid only when dealing with unbeamed
luminosities or (in
an approximate way) when the effect of beaming is not very strong because the
objects are viewed off-axis, as in this case.
For the 3CR sample, in which beaming is unimportant,
Barthel (1989)
found
 = 44°.4 from the ratio of
quasars to radio galaxies in the interval 0.5 < z < 1.
= 44°.4 from the ratio of
quasars to radio galaxies in the interval 0.5 < z < 1.
Table 3 summarizes the beaming parameters for the
radio band for different
classes of objects (see Sec. 6.2 for a
discussion of the
parameters for the BL Lac class). Note that we have used p = 3 +
 (see
Appendix B); using instead p = 2
+
(see
Appendix B); using instead p = 2
+  results in the Lorentz factors
extending to higher values
(Padovani and Urry
1992),
and in a slightly larger critical angle.
results in the Lorentz factors
extending to higher values
(Padovani and Urry
1992),
and in a slightly larger critical angle.
From the observed values of R we can estimate a lower limit to
the maximum Lorentz factor
(Appendix C). The FR II galaxy OD -159 is the most
lobe-dominated source in the 2 Jy sample. The most core-dominated FSRQ known
is 0400+258, which does not actually belong to the 2 Jy sample (its 2.7 GHz
flux ~ 1.5 Jy); its measured R is comparable to the lower limits (when
no extended emission was detected) for some of the 2 Jy FSRQ. For these two
objects, the R-values, K-corrected [Eq. (C2)] and extrapolated
(when necessary)
to 2.7 GHz rest frequency assuming  core -
core -  ext = -1,
are Rmin, FR IIs < 6 x 10-5
(OD -159;
Morganti et al. 1993)
and Rmax, FSRQ
ext = -1,
are Rmin, FR IIs < 6 x 10-5
(OD -159;
Morganti et al. 1993)
and Rmax, FSRQ  1000
(0400+258;
Murphy et al. 1993).
Using Eq. (C8),
we find
1000
(0400+258;
Murphy et al. 1993).
Using Eq. (C8),
we find  max > (1.7
x 107 21-p)1/2p ~ 13 for p = 3.
max > (1.7
x 107 21-p)1/2p ~ 13 for p = 3.
For these observed R values, small values of p imply high
values for the
largest Lorentz factor (here, for p = 2,  max
max  54). More
precisely,
54). More
precisely,  r
r  -0.3 for the 2 Jy FSRQ
(Padovani and Urry
1992)
so p
-0.3 for the 2 Jy FSRQ
(Padovani and Urry
1992)
so p  1.7 - 2.7
if p ranges between 2 +
1.7 - 2.7
if p ranges between 2 +  and 3 +
and 3 +  .
Then
.
Then  max
max  17 (for
p = 2.7) or
17 (for
p = 2.7) or  120
(for p = 1.7). The
need for quite high values of the largest
120
(for p = 1.7). The
need for quite high values of the largest  s for smaller values of p
was noted by
Urry et al. (1991a)
and
Padovani and Urry
(1992)
from their fits to the observed LFs.
s for smaller values of p
was noted by
Urry et al. (1991a)
and
Padovani and Urry
(1992)
from their fits to the observed LFs.
While the SSRQ-FSRQ-only scheme (ignoring the radio galaxies;
Orr and Browne 1982)
can not be ruled out, it is much harder to reconcile with the available
data, mainly because there seem to be too few SSRQ for them to be the parents
of FSRQ
(Padovani and Urry
1992).
The FR II-SSRQ-FSRQ scheme, illustrated by
the curves in Fig. 14, can be
tested further via the predicted
radio counts of flat- and steep-spectrum quasars, which converge at easily
accessible levels
(Padovani and Urry
1992).
15 There
is actually a range of critical angles, one for each  [Eq. (C4)]. The larger the Lorentz factor, the smaller the critical
angle;
[Eq. (C4)]. The larger the Lorentz factor, the smaller the critical
angle;  c (
c ( 1) = 14° is the
largest angle within
which an FR II would be identified as an FSRQ.
Using this angle is appropriate for our purposes because
the fitted distribution of Lorentz factors is skewed to low values.
Back.
1) = 14° is the
largest angle within
which an FR II would be identified as an FSRQ.
Using this angle is appropriate for our purposes because
the fitted distribution of Lorentz factors is skewed to low values.
Back.



 (the Lorentz factor) and
f (the fraction of luminosity intrinsic to
the jet) to match the observed luminosity function of FSRQ. It was
not possible to fit the observed FSRQ luminosity function with a single
Lorentz factor; it required instead a distribution in the range 5
(the Lorentz factor) and
f (the fraction of luminosity intrinsic to
the jet) to match the observed luminosity function of FSRQ. It was
not possible to fit the observed FSRQ luminosity function with a single
Lorentz factor; it required instead a distribution in the range 5 

 40, weighted toward low
values: n (
40, weighted toward low
values: n ( )
) 
 -2.3, with a mean
value <
-2.3, with a mean
value <  >
>  11 and
f
11 and
f  5 x 10-3.
[Note that this last parameter is fixed by the
largest
5 x 10-3.
[Note that this last parameter is fixed by the
largest  and by the maximum
value of the ratio between beamed and unbeamed radio flux, R;
Eq. (C5).]
and by the maximum
value of the ratio between beamed and unbeamed radio flux, R;
Eq. (C5).]



 c(
c(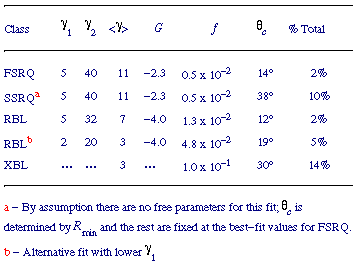
 0°. We take
0°. We take  (see
(see
 54). More
precisely,
54). More
precisely,