


8. THE VIABILITY OF UNIFIED SCHEMES
On the whole, unified schemes for radio-loud AGN are very successful. But
there remain some potential problems, including disturbing trends in
the linear sizes of radio galaxies and quasars, a dependence on redshift of
the ratio of quasars to radio galaxies, the lack of superluminal motion in
radio galaxies, and the un-FR-I-like radio morphologies of some BL Lac objects.
A number of complications also exist, like the need to include
evolution in unified schemes (the critical angle separating different AGN
classes or the ratio of Ljet /  ext may well depend on
redshift), even as the relatively simple beaming models adopted so far are
underconstrained by existing data. In this section we review known problems
for unified schemes and anticipate complications that should be addressed
when there are more complete data for larger samples of radio-loud AGN.
ext may well depend on
redshift), even as the relatively simple beaming models adopted so far are
underconstrained by existing data. In this section we review known problems
for unified schemes and anticipate complications that should be addressed
when there are more complete data for larger samples of radio-loud AGN.
8.1 Potential Problems with Unification
8.1.1 Linear Sizes of Blazars and Radio Galaxies
In principle, the linear sizes of radio sources can be used to test
unification because blazars oriented at small angles to the line of sight
should have systematically smaller large-scale radio structures than radio
galaxies in the plane of the sky. Right at the start, however, we must say
that conclusions regarding the relative linear sizes of blazars and radio
galaxies are extremely murky, having been the subject of quite a number of
papers, with often contradictory results
(Gopal-Krishna and
Kulkarni 1992;
Barthel 1989;
Kapahi 1987;
Kapahi 1989;
Kapahi 1990;
Barthel and Miley 1988;
Onuora 1989;
Onuora 1991;
Hough and Readhead
1989;
Nilsson et al. 1993,
and references therein). It turns out that the linear size depends, not
unexpectedly, on several factors like radio power and redshift. Even matching
these variables, the expected difference in mean linear size is quite modest,
only a factor of 2 for an orientation of 30° compared to 90°,
while the scatter in intrinsic sizes must be many times that large.
In a recent work,
Singal
(1993a; see also
Singal 1988)
studied the linear sizes of a large, heterogeneous sample of
radio galaxies (about half of which have redshifts estimated from the
magnitude-redshift relation) and quasars. His main result is that both
size-luminosity and size-redshift correlations are significantly different for
the two classes. In particular, luminosity and size are directly correlated
for radio galaxies and inversely correlated for quasars, while the size of
radio galaxies falls strongly with redshift and not at all for quasars.
According to Singal, the only redshift range for which unification works is
0.5 < z < 1, the interval
Barthel (1989)
used in his original analysis of
the 3CR catalog ostensibly because of the better statistics there. Indeed,
for the lowest luminosity bin and z  0.4,
Singal (1993a)
found that the median linear size of quasars is larger than that of
radio galaxies, completely opposite to the predictions of the unified scheme.
0.4,
Singal (1993a)
found that the median linear size of quasars is larger than that of
radio galaxies, completely opposite to the predictions of the unified scheme.
These results, however, are uncertain and/or contradict other comparable work.
One problem with determining linear sizes is that often the radio source
morphology is unclear or the source is poorly resolved. In a similar study
limited to sources with clear FR II double structures, which by definition
have sharp outer boundaries,
Nilsson et al. (1993)
found quite different results for the dependence of linear size on
redshift and luminosity; in direct contrast to
Singal (1993a),
the median values of the linear size
for quasars are (marginally) smaller than for galaxies in all luminosity bins.
Another issue is the use of complete flux-limited samples. The 3CR catalog
is excellent for this purpose because it is largely unbiased by beamed
flux. From the luminosity function analysis we found quasars
(effectively SSRQ) and radio galaxies are divided at
 c ~ 38°
(Table 3);
the mean angle for SSRQ (between 14° and ~ 38°)
is therefore 28° and the mean angle for FR IIs is 66°.
The ratio of quasar linear size to radio galaxy linear size,
1.9 for these mean angles,
is both small and a very weak function of critical angle.
Estimating the critical angle from the numbers of quasars and radio
galaxies in the 3CR gives
c ~ 38°
(Table 3);
the mean angle for SSRQ (between 14° and ~ 38°)
is therefore 28° and the mean angle for FR IIs is 66°.
The ratio of quasar linear size to radio galaxy linear size,
1.9 for these mean angles,
is both small and a very weak function of critical angle.
Estimating the critical angle from the numbers of quasars and radio
galaxies in the 3CR gives  c = 44.4 °
(Barthel 1989),
with a 1
c = 44.4 °
(Barthel 1989),
with a 1  uncertainty of ± 6.6°;
this gives a foreshortening factor of 1.9+0.3-0.2.
The foreshortening factor would be much larger were one to compare
only FSRQ and FR IIs, but there are too few FSRQ in the 3CR and using
the 2 Jy sample would mean incorporating the selection bias of beaming, which
is nontrivial.
uncertainty of ± 6.6°;
this gives a foreshortening factor of 1.9+0.3-0.2.
The foreshortening factor would be much larger were one to compare
only FSRQ and FR IIs, but there are too few FSRQ in the 3CR and using
the 2 Jy sample would mean incorporating the selection bias of beaming, which
is nontrivial.
Another complication is that even modest misalignments between large-scale
radio structure and the obscuring torus are enough to confuse the expected
linear size trend
(Gopal-Krishna et
al. 1994).
For example, the distributions
of observed linear size and bend angle for a large, heterogeneous sample of
quasars and radio galaxies are completely consistent with random
orientations within
and without a cone angle of ~ 50°, respectively, assuming only that
the jets have small intrinsic bend angles ( 25°) and modest
intrinsic arm-length differences
(Lister et al. 1994a).
In sum, considering the many problems and potential complications, it is
remarkable that the analysis of
linear sizes of quasars and FR IIs gives any sensible results at all.
25°) and modest
intrinsic arm-length differences
(Lister et al. 1994a).
In sum, considering the many problems and potential complications, it is
remarkable that the analysis of
linear sizes of quasars and FR IIs gives any sensible results at all.
The comparison of linear sizes of FR I galaxies and BL Lac objects is even
more difficult because the amorphous FR I radio structures have no clear outer
boundaries. The largest angular sizes of the EMSS BL Lacs are similar to those
of B2 FR Is and of a heterogeneous sample of radio-selected BL Lacs
(Perlman and Stocke
1993),
in apparent contradiction to their unification. This may be
due to substantial misalignments between the parsec and kiloparsec scale jets
(Perlman and Stocke
1993),
which are quite common in BL Lacs
(Kollgaard et
al. 1992).
In that case, a small angle to the line of sight of the VLBI jet
does not necessarily imply a very small radio linear size.
In addition, if the bulk Lorentz factors in BL Lac objects are small
(Sec. 6.3), the critical angle separating
them from FR Is can
be quite large. For example, for  ~ 2 and f ~ 0.05,
~ 2 and f ~ 0.05,
 c ~ 19°
(Table 3).
The corresponding ratio of projected lengths of BL Lacs
and FR Is, evaluated at the mean angle (ignoring beaming)
is ~ 3; for the XBL fit in
Table 3 it is ~ 2.5.
c ~ 19°
(Table 3).
The corresponding ratio of projected lengths of BL Lacs
and FR Is, evaluated at the mean angle (ignoring beaming)
is ~ 3; for the XBL fit in
Table 3 it is ~ 2.5.
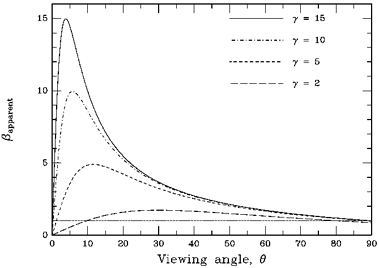
|
Figure 21. The apparent velocity relative to the speed of
light versus angle to
the line of sight for an emitter approaching at relativistic speed.
Different curves correspond to different Lorentz factors: from the top down,
 = 15, 10, 5, 2. The dotted
line corr esponds to = 15, 10, 5, 2. The dotted
line corr esponds to  a = 1.
Note that a = 1.
Note that  a is essentially independent of a is essentially independent of
 at large angles. at large angles.
|
In the end, consideration of linear sizes of radio sources is not a compelling
test of unified schemes. Even the oft-stated problem of large deprojected
radio sizes - wherein the lengths of superluminal sources and/or
one-sided jets as large as ~ 1 Mpc in length (like NGC 6251) are thought
to be uncomfortably large when deprojected by their orientation angles -
vanishes when one thinks about
the numbers. Neither superluminal motion nor one-sidedness require a
particularly
small angle [Fig. 21 and Eq. (A4), Eq. (A8)],
and in fact the expected deprojection correction is only a factor of 2 or so.



 ext may well depend on
redshift), even as the relatively simple beaming models adopted so far are
underconstrained by existing data. In this section we review known problems
for unified schemes and anticipate complications that should be addressed
when there are more complete data for larger samples of radio-loud AGN.
ext may well depend on
redshift), even as the relatively simple beaming models adopted so far are
underconstrained by existing data. In this section we review known problems
for unified schemes and anticipate complications that should be addressed
when there are more complete data for larger samples of radio-loud AGN.



 0.4,
0.4,
 c ~ 38°
(
c ~ 38°
( uncertainty of ± 6.6°;
this gives a foreshortening factor of 1.9+0.3-0.2.
The foreshortening factor would be much larger were one to compare
only FSRQ and FR IIs, but there are too few FSRQ in the 3CR and using
the 2 Jy sample would mean incorporating the selection bias of beaming, which
is nontrivial.
uncertainty of ± 6.6°;
this gives a foreshortening factor of 1.9+0.3-0.2.
The foreshortening factor would be much larger were one to compare
only FSRQ and FR IIs, but there are too few FSRQ in the 3CR and using
the 2 Jy sample would mean incorporating the selection bias of beaming, which
is nontrivial.
 25°) and modest
intrinsic arm-length differences
(
25°) and modest
intrinsic arm-length differences
( ~ 2 and f ~ 0.05,
~ 2 and f ~ 0.05,

 a = 1.
Note that
a = 1.
Note that